
- •Лекция 1 предел последовательности
- •1 Понятие числовой последовательности. Предел числовой последовательности. Свойства сходящихся числовых последовательностей
- •Свойства сходящихся последовательностей
- •2 Бесконечно большие и бесконечно малые числовые последовательности. Основные способы вычисления пределов
- •Свойства бесконечно больших и бесконечно малых последовательностей:
- •Основные способы вычисления пределов:
- •Лекция 2 предел функции
- •1 Предел функции в точке. Односторонние пределы. Предел функции в бесконечности
- •2 Бесконечно малые и бесконечно большие функции. Замечательные пределы
- •Свойства бесконечно малых и бесконечно больших функций
- •Первый и второй замечательные пределы
- •3 Непрерывность функции в точке и на отрезке. Точки разрыва функции и их классификация
- •Свойства функций, непрерывных в точке:
- •Непрерывность функции на отрезке
- •Свойства функций, непрерывных на отрезке
- •Точки разрыва функции и их классификация
- •Лекция 3 производная функции
- •1 Производная функции, ее геометрический и экономический смысл. Основные правила дифференцирования. Производные основных элементарных функций
- •Основные правила дифференцирования
- •2 Логарифмическое дифференцирование. Производная неявной функции. Производные высших порядков
- •Лекция 4 правило лопиталя. Дифференциал функции
- •1 Раскрытие неопределенностей при помощи правила Лопиталя
- •2 Дифференциал функции, его геометрический смысл. Применение дифференциала в приближенных вычислениях
- •Лекция 5 исследование функций
- •1 Локальные экстремумы функции. Достаточные условия экстремума функции
- •2 Исследование функций на выпуклость и вогнутость. Точка перегиба
- •3 Асимптоты графика функции
- •4 Общая схема построения графика функции
- •Лекция 6 функции нескольких переменных
- •1 Предел и непрерывность функции двух переменных
- •2 Частные производные первого порядка. Полный дифференциал. Частные производные высших порядков
- •3 Экстремум функции нескольких переменных. Необходимые и достаточные условия существования экстремума
- •Лекция 7 НеоПределенный иНтеграл
- •1 Первообразная и неопределенный интеграл. Таблица основных неопределенных интегралов
- •Основные свойства неопределенного интеграла
- •2 Основные методы интегрирования
- •Лекция 8 НеоПределенный иНтеграл (продолжение)
- •1 Интегрирование выражений, содержащих квадратный трехчлен
- •2 Интегрирование простейших рациональных дробей. Интегрирование простейших иррациональных функций
- •Интегрирование простейших иррациональных функций
- •3 Интегрирование тригонометрических функций
- •Лекция 9 оПределенный иНтеграл
- •1 Определенный интеграл и его геометрический смысл. Основные свойства определенного интеграла
- •Геометрический смысл определенного интеграла
- •Основные свойства определенного интеграла
- •Формула Ньютона-Лейбница
- •2 Основные способы вычисления определенного интеграла Замена переменной в определенном интеграле
- •Интегрирование по частям
- •Доказательство
- •3 Вычисление площадей плоских фигур, объемов тел вращения, длин дуг плоских кривых Площадь криволинейной трапеции
- •Объем тела вращения
- •Длина дуги плоской кривой
- •Лекция 10 несобственные интегралы
- •1 Несобственные интегралы с бесконечными пределами интегрирования
- •2 Несобственные интегралы от неограниченных функций
- •Лекция 11 дифференциальные уравнения первого порядка
- •1 Дифференциальные уравнения первого порядка. Задача Коши
- •2 Дифференциальные уравнения с разделяющимися переменными
- •3 Линейные дифференциальные уравнения первого порядка
- •1 Метод подстановки (метод Бернулли).
- •2 Метод вариации произвольной постоянной (метод Лагранжа)
- •Лекция 12 дифференциальные уравнения высших порядков
- •1 Интегрирование дифференциальных уравнений высших порядков, допускающих понижение порядка
- •2 Однородные и неоднородные линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Лекция 13 числовые ряды
- •Числовой ряд. Сходимость. Признаки сходимости
- •1 Определение числового ряда. Сходимость. Основные свойства числовых рядов
- •Основные свойства числовых рядов
- •2 Ряды с положительными членами. Признаки сходимости
- •3 Знакочередующиеся и знакопеременные ряды
- •Лекция 14 степенные ряды
- •Ключевые понятия
- •1 Определение степенного ряда. Теорема Абеля
- •2 Свойства степенных рядов
- •3. Ряды Тейлора, Маклорена для функций
- •Разложение некоторых элементарных функций в ряд Маклорена
- •Приложения степенных рядов
- •Список литературы
- •Содержание
- •Лекция 13 Числовые ряды………….……………………………………..93
- •Лекция 14 Степенные ряды……………………...……….………………103
- •Список литературы…………..…………….……...………………………..112
- •220086, Минск, ул. Славинского, 1, корп. 3.
Лекция 3 производная функции
План
1 Производная функции, ее геометрический и экономический смысл. Основные правила дифференцирования. Производные основных элементарных функций.
2 Логарифмическое дифференцирование. Производная неявной функции. Производные высших порядков.
Ключевые понятия
|
Правила дифференцирования. Производная функции. Уравнение касательной. Уравнение нормали. |
Производные суммы, произведения, частного двух функций. Производная сложной функции. Производные высших порядков. |
1 Производная функции, ее геометрический и экономический смысл. Основные правила дифференцирования. Производные основных элементарных функций
Пусть функция f(х) определена в некоторой окрестности точки х0.
Определение 1 Производной функции f(х) в точке х0 называется число, обозначаемое f (х0) и равное
![]() ,
(1)
,
(1)
если этот предел существует.
Так как х = х0 + ∆х, х – х0 = ∆х, то предел (1) может быть записан в виде
![]() ,
(2)
,
(2)
т. е. производная функции f(x) в точке х0 есть предел отношения ее приращения ∆f(х0) в этой точке к соответствующему приращению аргумента ∆х, когда ∆х стремится к нулю.
Для обозначения производной функции f(x) в точке х0 используют следующие выражения:
![]() .
.
Определение 2 Правой производной называется число
![]() .
(3)
.
(3)
Аналогично
определяется левая
производная
![]() .
.
Заметим, что существование производной функции в точке равносильно равенству ее односторонних производных в этой точке.
Пример
1
Используя
определение производной, найти
![]() для функции f(x)
= 4x2
– 1.
для функции f(x)
= 4x2
– 1.
Решение.
![]()
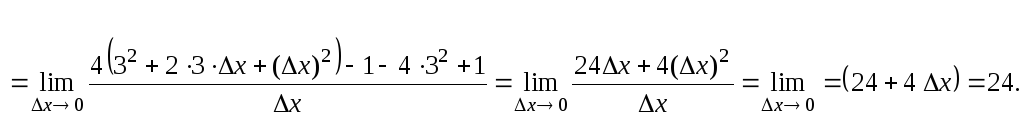
Ответ:
![]() = 24.
= 24.
Пример 2 Найти односторонние производные функции f(x) = | x | в точке х0 = 0.
Решение:
![]()
![]()
Таким образом, функция f(x) = | x | в точке х0 = 0 не имеет производной, так как односторонние производные не совпадают.
Ответ:
![]() = 1,
= 1,
![]()
Выясним геометрический смысл производной.
Пусть f(х) – непрерывная функция, определенная в некоторой окрестности точки х0. Рассмотрим две точки А (х0; f(х0)) и В (х1; f(х1)), лежащие на графике функции f(х).
Прямая l = АВ называется секущей. Запишем ее уравнение, используя уравнение прямой, заданной двумя точками:
l:
![]() .
.
Выразим из этого уравнения у:
![]() ,
(4)
,
(4)
где
![]()

Пусть точка В стремится к точке А по графику функции f(x). Тогда секущая АВ будет стремиться к некоторому предельному положению. Это предельное положение секущей называется касательной к графику функции f(x) в точке х0, если существует конечный предел
![]() ,
,
который называется угловым коэффициентом касательной к графику функции f(x) в точке х0. Из (4) следует, что
![]() (5)
(5)
– уравнение касательной к графику f(x) в точке х0.
Таким
образом,
![]() ,
,
где α – угол наклона касательной к положительному направлению оси Ох.
Следовательно, с геометрической точки зрения, производная функции f(x) в точке х0 численно равна тангенсу угла, образованного касательной к графику функции f(x) в точке х0 и положительным направлением оси Ох.
Если касательная образует угол 90о с положительным направлением оси Ох, то будем говорить, что функция имеет в данной точке производную, равную .
Определение
3 Прямая,
перпендикулярная к касательной графика
функции f(x)
в точке
![]() ,
называется нормалью
к кривой, определяемой функцией f(x)
в точке х0.
Учитывая, что для перпендикулярных
прямых k1k2
= –1, из уравнения (5) получаем уравнение
нормали к
графику функции f(x)
в точке х0:
,
называется нормалью
к кривой, определяемой функцией f(x)
в точке х0.
Учитывая, что для перпендикулярных
прямых k1k2
= –1, из уравнения (5) получаем уравнение
нормали к
графику функции f(x)
в точке х0:
![]() .
(6)
.
(6)
Определение 4 Углом φ между двумя кривыми у = f1(х) и у = f2(х) в точке их пересечения с абсциссой х0 назовем угол между касательными к этим кривым, проведенными к ним в этой точке:
![]() . (7)
. (7)
Выясним теперь экономический смысл производной.
Пусть
функция у
= f(х)
устанавливает зависимость объема
выпуска продукции от затрат ресурса
х,
а ресурс х
получает прирост Δх.
Тогда
![]() будет приращением выпуска продукции,
а отношение
будет приращением выпуска продукции,
а отношение
![]() – средним приращением выпуска продукции
на единицу затрат.
– средним приращением выпуска продукции
на единицу затрат.
Следовательно,
производная
![]() выражает предельный продукт при затратах
х
и представляет собой приближенно
дополнительный выпуск продукции на
единицу дополнительных затрат.
выражает предельный продукт при затратах
х
и представляет собой приближенно
дополнительный выпуск продукции на
единицу дополнительных затрат.
Если функция у = f (t) выражает количество произведенной продукции за время t, то f (t) есть предельная производительность в момент времени t. Аналогичным образом могут быть определены предельные издержки, предельный доход, предельная выручка и т. д.
Отметим,
что если функция f(х)
имеет производную в точке х0,
то она непрерывна в этой точке.
Действительно, так как
![]() ,
то
,
то
![]() ,
где
,
где
![]() =
0 (теорема о связи предела функции и
бесконечно малой функции).
=
0 (теорема о связи предела функции и
бесконечно малой функции).
Следовательно,
![]()
![]() т.
е. по необходимому и достаточному
условию непрерывности функции в точке
х0
функция f(х)
непрерывна в точке х0.
т.
е. по необходимому и достаточному
условию непрерывности функции в точке
х0
функция f(х)
непрерывна в точке х0.
Определение 5 Операция вычисления производной функции называется дифференцированием.
