
- •Глава 9 неопределенный интеграл
- •§ 1. Первообразная функции.
- •§ 2. Основные методы интегрирования.
- •§ 3. Многочлены. Рациональные дроби. Простейшие рациональные дроби.
- •§ 4. Интегрирование простейших рациональных дробей.
- •§ 5. Разложение рациональной дроби на простейшие. Интегрирование рациональных дробей.
- •§ 6. Интегрирование некоторых иррациональных функций.
- •§ 7. Интегрирование тригонометрических функций.
- •Решение практических задач
- •Примеры для самостоятельного решения.
§ 4. Интегрирование простейших рациональных дробей.
Определение 7. Правильные рациональные дроби вида:
I.
![]() II.
II.
![]() .
.
III.
![]() IV.
IV.
![]()
(в дробях III, IV видов знаменатель действительных корней не имеет) называются простейшими дробями I, II, III, IV типов.
I.
![]()
II.
![]()
III.
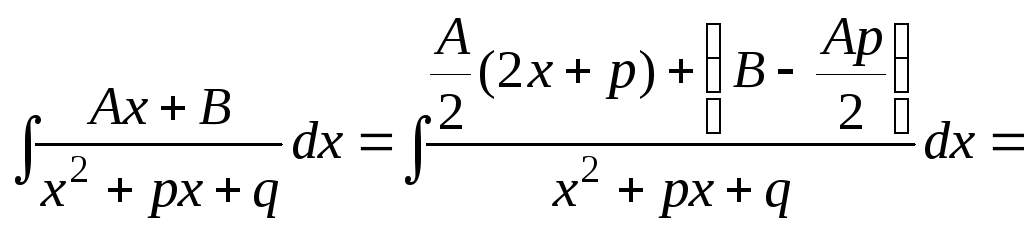
![]()
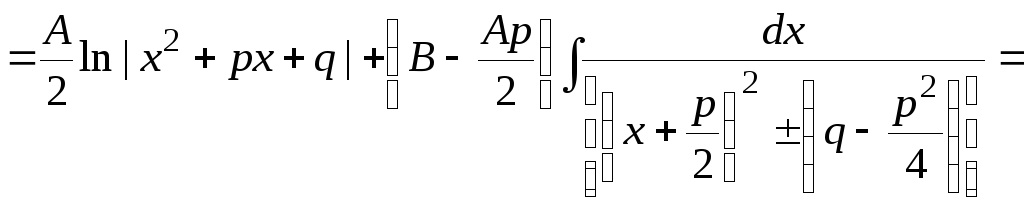
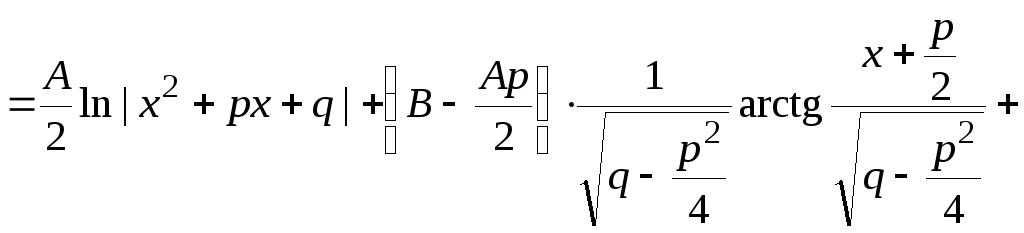
![]()
§ 5. Разложение рациональной дроби на простейшие. Интегрирование рациональных дробей.
Т е о р е м а 6. Пусть дана правильная рациональная дробь
![]()
Если
![]() ,
то дробь
,
то дробь
![]() может быть представлена в виде
может быть представлена в виде
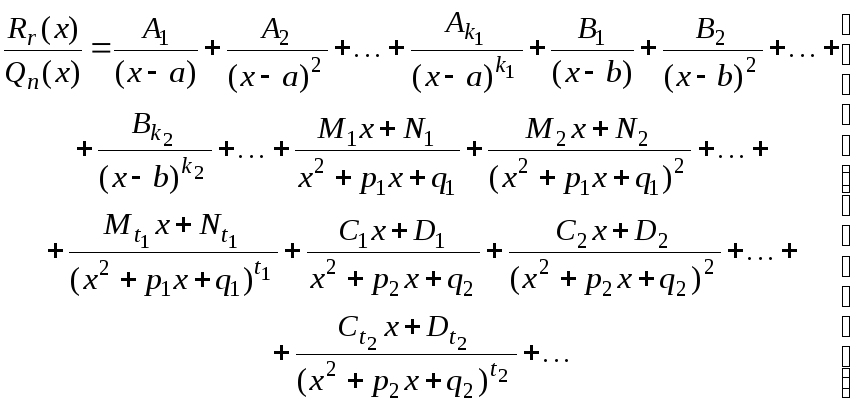 (9.3)
(9.3)
Разложение (3) называется разложением рациональной функции на элементарные (простейшие) дроби. Чтобы определить числа
![]()
правую часть
разложения приводят к общему знаменателю
и числители левой и правой дробей
приравнивают. Так как равенство между
многочленом
![]() и многочленом, который получится в
правой части, справедливо для всех х,
то коэффициенты при одинаковых степенях
х
этих многочленов равны между собой.
Таким образом, получим ряд уравнений
первой степени, из которых найдем
неизвестные числа. Этот метод нахождения
коэффициентов называется методом
неопределенных коэффициентов.
и многочленом, который получится в
правой части, справедливо для всех х,
то коэффициенты при одинаковых степенях
х
этих многочленов равны между собой.
Таким образом, получим ряд уравнений
первой степени, из которых найдем
неизвестные числа. Этот метод нахождения
коэффициентов называется методом
неопределенных коэффициентов.
Пусть требуется
вычислить интеграл от рациональной
дроби
![]() ,
т. е.
,
т. е.
![]() .
.
Интеграл от рациональной дроби вычисляется согласно следующим основным правилам:
1. Если рациональная дробь неправильная, то ее представляют в виде суммы многочлена и правильной рациональной дроби.
2. Разлагают знаменатель правильной рациональной дроби на множители.
3. Правильную рациональную дробь раскладывают на сумму простейших дробей, т. е. сводят интегрирование правильной рациональной дроби к интегрированию простейших дробей.
§ 6. Интегрирование некоторых иррациональных функций.
Интегралы от некоторых иррациональных функций с помощью определенных подстановок приводятся к интегралам рациональных функций и, следовательно, до конца интегрируются.
|
Вид интеграла |
Замена переменной в интеграле |
|
1.
R – рациональная функция своих аргументов. |
t k = x, тогда d x = k∙t k – 1 d t, где k – общий знаменатель всех дробных показателей у переменной х. В результате получаем интеграл от рациональной дроби. |
|
2.
|
ax + b = tk , тогда a∙dx = k∙t k – 1d t, где k – общий знаменатель всех дробных показателей у переменной х. |
|
3.
|
|
|
4.
|
x = a sin t. Полезно знать формулу
|
|
5.
|
x = a tg t. Полезно знать формулу
|
|
6.
|
x
= a
sec
t
=
Полезно знать формулу
|
§ 7. Интегрирование тригонометрических функций.
|
Вид интеграла |
Способ решения |
|
1.
|
Универсальные тригонометрические подстановки (общий случай)
В результате получится интеграл от рациональной функции. |
|
2.
|
|
|
3.
|
|
|
4.
|
|
|
5.
sin x, cos x входят только в четных степенях. |
t
= tg
x,
|
|
6.
а) по крайней мере, одна из m и n – нечетна. Пусть п = 2k+1. |
|
|
б) m, n – четные, больше нуля, т. е. m = 2p, n = 2q. |
Воспользоваться формулами понижения степени
|
|
в) n, m – четные и хотя бы один отрицателен. |
Вводится замена tg x = t или ctg x = t. |
|
7.
|
Воспользоваться формулами
|

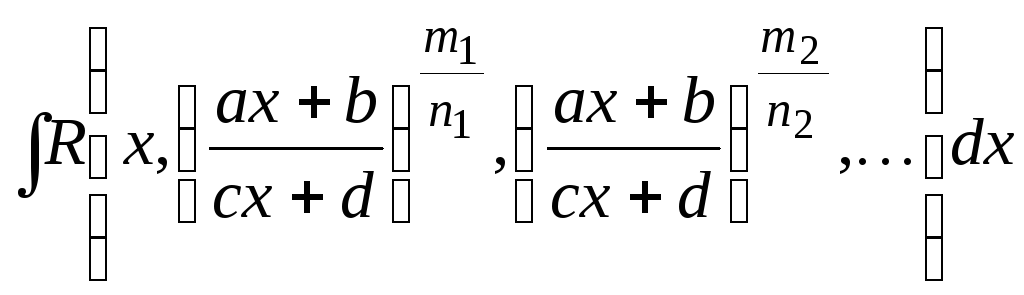
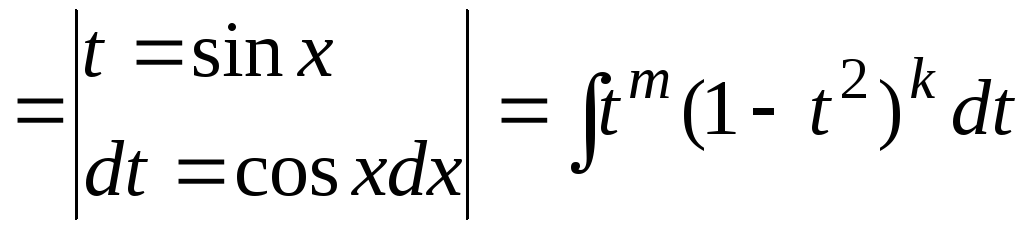 – интеграл от
рациональной функции.
– интеграл от
рациональной функции.