
- •Литература основная
- •Литература дополнительная
- •1. Современные системы связи
- •1.1. Виды направляющих систем электросвязи.
- •1.2. Принцип телефонной связи. Системы многоканальной передачи по линиям связи
- •1.3. Классификация кабелей связи. Основные конструктивные элементы кабелей связи
- •Классификация симметричных кабелей связи
- •Междугородные симметричные кабели
- •2. Зоновые (внутриобластные) кабели.
- •Городские телефонные кабели.
- •4. Кабели сельской и проводного вещания
- •Элементы конструкций коаксиальных кабелей связи (кк)
- •1. Магистральные коаксиальные кабели
- •2. Зоновые (внутриобластные) коаксиальные кабели
- •2. Электродинамика направляющих систем
- •2.1 Основные положения. Основные уравнения электромагнитного поля
- •2.2. Метод комплексных амплитуд. Уравнения Максвелла в комплексной форме. Однородные волновые уравнения для векторов e и h.
- •2.3. Эмп в диэлектрике (а )
- •2.4. Эмп в диэлектрике (а)
- •2.5. Классы электромагнитных волн направляющих систем. Исходные принципы расчета направляющих систем
- •3 Двухпроводные направляющие системы.
- •3.1 Основное уравнение однородной кабельной цепи
- •3.2 Вторичные параметры двухпроводных направляющих систем
- •3.2.1 Волновое сопротивление
- •3.2.2 Коэффициент распространения
- •3.2.3. Скорость распространения электромагнитной энергии по кабелям.
- •3.3 Свойства неоднородных линий
- •3.3.1 Падающие, отраженные и стоячие волны
- •3.3.2 Входное сопротивление и рабочее затухание кабельной линии
- •3.3.2 Рабочее затухание кабельной линии
- •3.3.3 Линии неоднородные по длине
- •3.3.4 Качество передачи и дальность связи по кабельным линиям
- •3.4 Симметричные кабели
- •3.4.2. Определение сопротивления и индуктивности цепи симметричного кабеля
- •Определение емкости и проводимости симметричной цепи
- •3.5 Коаксиальные кабели связи
- •3.5.1 Электрические процессы в коаксиальных кабелях связи
- •3.5.2 Определение сопротивления и индуктивности коаксиальной цепи
- •3.5.5 Конструктивные неоднородности в коаксиальных кабелях
- •3.6 Взаимное влияние между симметричными кабельными цепями.
- •Для одной строительной длины
- •3.6.3. Способы увеличения переходных затуханий.
- •3.6.4 Защита цепей симметричных кабелей связи от взаимных влияний методом скрутки.
- •3.6.5 Симметрирование кабелей связи
- •Коэффициенты асимметрии
- •3.7 Взаимные влияния между коаксиальными цепями
- •3.8 Экранирование
- •Экранирующее действие оболочки относительно внешних помех
- •Волоконно-оптические кабели
- •1. Основные положения. Световоды.
- •2. Лучевая теория передачи по световодам.
- •3. Волновая теория передачи по световодам.
- •4. Затухание световодов.
- •4.3.5 Дисперсия.
2.2. Метод комплексных амплитуд. Уравнения Максвелла в комплексной форме. Однородные волновые уравнения для векторов e и h.
Все реальные электромагнитные процессы можно представить либо в виде суммы дискретных гармонических колебаний, либо в виде непрерывного спектра гармонических колебаний. Поэтому изучение гармонических электромагнитных полей представляет большой практический и теоретический интерес. Такие поля часто называют также монохроматическими.
Пусть
вектор поля
![]() изменяются по косинусоидальному закону,
причем фазы всех трех прямоугольных
проекций одинаковы, т.е. волна линейно
поляризована, тогда выражение для
изменяются по косинусоидальному закону,
причем фазы всех трех прямоугольных
проекций одинаковы, т.е. волна линейно
поляризована, тогда выражение для
![]() запишется
запишется
![]() ,
,
где
![]() – единичные вектора-орты по направлениям
x,
y,
z,
соответственно;
– единичные вектора-орты по направлениям
x,
y,
z,
соответственно;
![]() ,
,
![]() ,
,
![]() – амплитуды;
– амплитуды;
![]() – фаза; – циклическая
или круговая частота гармонических
колебаний. Амплитуды и фаза не зависят
от времени, а только от координат x,
y,
z.
– фаза; – циклическая
или круговая частота гармонических
колебаний. Амплитуды и фаза не зависят
от времени, а только от координат x,
y,
z.
Обозначим

Комплексной
амплитудой вектора
![]() назовем вектор
назовем вектор
![]() .
.
Тогда
мгновенное значение вектора
![]() определится по формуле
определится по формуле
![]() .
.
Аналогично можно записать комплексную амплитуду напряженности магнитного поля
![]()
и мгновенное значение
![]() .
.
Рассмотрим первое уравнение Максвелла
![]() .
.
Подставив вместо
![]() величину
величину
![]() ,
реальная часть которой равна
,
реальная часть которой равна
![]() ,
а вместо
,
а вместо
![]() величину
величину
![]() ,
то получим
,
то получим
![]() .
.
После
сокращения на
![]() получается первое уравнение Максвелла
в комплексной форме записи (для комплексных
амплитуд)
получается первое уравнение Максвелла
в комплексной форме записи (для комплексных
амплитуд)
![]()
или
![]() ,
,
где
![]() –
комплексная д/э проницаемость,
–
комплексная д/э проницаемость,
 здесь
здесь
![]() –тангенс угла д/э потерь.
–тангенс угла д/э потерь.
Аналогично получаются и остальные уравнения ЭМП в комплексной форме записи
![]() ,
,
![]() ,
,
![]() .
.
Решив
эти уравнения и определив комплексные
амплитуды
![]() и
и
![]() ,
легко найти мгновенные значения векторов
поля из соотношений
,
легко найти мгновенные значения векторов
поля из соотношений
![]() ,
,
![]() .
.
Преимущество
комплексной формы записи основных
уравнений поля заключается в том, что
время
![]() исключается из этих уравнений, что
значительно упрощает решение задач
электродинамики.
исключается из этих уравнений, что
значительно упрощает решение задач
электродинамики.
В дальнейшем для упрощения записи при переходе к мгновенным значениям комплексные амплитуды будут обозначаться как
![]()
![]()
а без перехода к мгновенным значениям
![]()
![]()
Уравнения Максвелла в комплексной форме записи в декартовой системе координат запишутся
 ,
,
 ,
,
![]() ,
,
![]() .
.
Однородные волновые уравнения имеют вид (уравнения Гельмгольца)
![]() ,
,
![]() ,
,
где
![]() – коэффициентом распространения в
среде, 1/м.
– коэффициентом распространения в
среде, 1/м.
В
волновых уравнениях оператор
![]() называется лапласианом. Лапласиан от
скалярной функции
в цилиндрической системе координат
запишется:
называется лапласианом. Лапласиан от
скалярной функции
в цилиндрической системе координат
запишется:
![]() .
.
Лапласиан от вектора является вектор. Его составляющими в декартовой системе координат является лапласиан от соответствующих компонент дифференцируемого вектора:
![]() .
.
В декартовой системе координат векторные волновые уравнения распадаются на шесть независимых скалярных волновых уравнений:
 .
.
Все эти уравнения имеют совершенно одинаковую форму. Поэтому для нахождения составляющих ЭМП достаточно решить лишь одно уравнение в частных производных, например:
![]()
Остальные
составляющие Е
и Н
определяются из
![]() непосредственно из уравнений Максвелла.
непосредственно из уравнений Максвелла.
2.3. Эмп в диэлектрике (а )
Идеальный
проводник – это среда с бесконечно
большой удельной проводимостью
![]() ,
а идеальный проводник – это среда, не
обладающая проводимостью
,
а идеальный проводник – это среда, не
обладающая проводимостью
![]() .
В идеальном проводнике может существовать
только ток проводимости:
.
В идеальном проводнике может существовать
только ток проводимости:
![]() ,
а в идеальном диэлектрике – только ток
смещения:
,
а в идеальном диэлектрике – только ток
смещения:
![]() .
В реальных средах имеется как ток
проводимости, так и ток смещения. Принято
среду считать проводящей, когда:
.
В реальных средах имеется как ток
проводимости, так и ток смещения. Принято
среду считать проводящей, когда:
![]() .
Диэлектрик характеризуется неравенством:
.
Диэлектрик характеризуется неравенством:
![]() .
.
Рассмотрим распространение гармонической электромагнитной энергии в идеальном диэлектрике ( = 0). Уравнения Максвелла для гармонических колебаний примут вид:
![]()
Волновые уравнения о декартовой системе координат получаются:
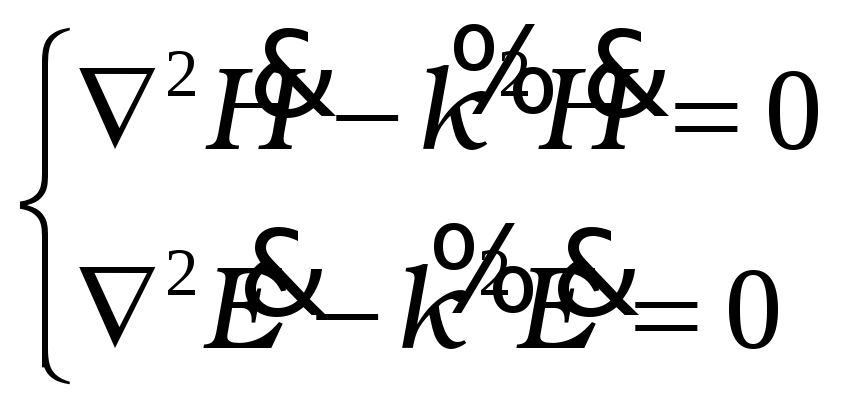 ;
;
здесь коэффициент
распространения:
![]() .
.
Рассмотрим
распространение плоской э/м волны в
однородном диэлектрике. Э/м волна
называется плоской, когда все величины,
характеризующие интенсивность э/м
процесса, зависят только от одной
декартовой координаты. Пусть волновой
процесс распространяется вдоль оси z.
Тогда поперечными по отношению к
направлению распространения являются
координаты x,
y.
При этом
![]() .
.
Решим
уравнение Гемгольца для вектора
![]() .
Примем, что
.
Примем, что
![]() ,
а
,
а
![]() .
Следовательно
.
Следовательно
![]() ,
а
,
а
![]() .
.
Тогда
волновые уравнения для компонент
![]() и
и
![]() запишутся
запишутся
![]() ;
;
![]() .
.
Решим
волновое уравнение относительно
![]() .
Общим решением этого уравнения является
суперпозиция двух частных решений
.
Общим решением этого уравнения является
суперпозиция двух частных решений
![]() ,
,
где
![]() – прямая волна;
– прямая волна;
![]() – обратная волна.
– обратная волна.
Коэффициент распространения можно записать
![]() ,
,
где
![]() – называется коэффициентом затухания
волны в среде;
– называется коэффициентом затухания
волны в среде;
![]() –
называется коэффициентом фазы волны в
среде.
–
называется коэффициентом фазы волны в
среде.
Для
идеального диэлектрика
![]() .
Здесь
.
Здесь
![]() называют волновым числом. Таким образом
называют волновым числом. Таким образом
![]() .
.
Мгновенное значение напряженности электрического поля запишется:
![]() .
.
Первое слагаемое здесь называется прямой волной, а второе - обратной.
Если
![]() и
и
![]() ,
то получается стоячая волна (см. рис.
2.1)
,
то получается стоячая волна (см. рис.
2.1)
![]() .
.

Рис. 2.1. Стоячая волна
Пусть обратная волна отсутствует, тогда изменение бегущей волны определяется по формуле:
![]() .
.
На рис. 2.2 представлено распределение бегущей волны Ех для двух моментов времени t1 и t2 = t1 + t.

Рис 2.2. Распределение бегущей волны Ех в моменты времени t1 и t2
Скорость перемещения фронта бегущей волны называется фазовой скоростью и определяется из условия равенства фаз двух косинусоид (см. рис. 2.2):
![]() ,
,
Откуда
![]() .
.
Тогда
![]() ,
,
поскольку
![]() ,
тогда получаем:
,
тогда получаем:
![]() ,
,
где
![]() – скорость электромагнитной волны в
вакууме (скорость света в вакууме), м/с.
– скорость электромагнитной волны в
вакууме (скорость света в вакууме), м/с.
Расстояние при прохождении которого волна изменяет стою фазу на 2, называется длиной волны и определяется из равенства:
![]() .
.
Тогда
![]() .
.
Напряженность
магнитного поля
![]() определяется из уравнения Максвелла
определяется из уравнения Максвелла

откуда
 .
.
Здесь
 – называется волновым сопротивлением.
– называется волновым сопротивлением.
Для вакуума = = 1; ZВ = 376,8 Ом
В общем случае волновое сопротивление комплексная величина.
