Операции над множествами

Для каждой пары множеств X и Y можно определить операцию объединения двух множеств ХY={х: хХ или хY}, т.е. ХY есть множество элементов, которые принадлежат или множеству X или множеству Y или тому и другому множествам вместе. Другими словами множество ХY состоит из элементов, которые принадлежат по крайней мере одному из множеств X, Y.

Пример. X = {0, 2, 3}, Y= {0, 3, 6, 7}, ХY = {0, 2, 3, 6, 7}.

Объединение множеств по аналогии с арифметическими действиями иногда называют сложением множеств. Из определения этой операции, очевидно, что объединение обладает свойствами перестановочности (коммутативности) ХY =YX и сочетаемости (ассоциативности)

(XY)Z = X(YZ), что позволяет записывать без скобок объединение любого количества множеств:

X₁X₂ ... X_n= {х: х  X₁ или х  X₂... или х  X_n}.

Операция пересечения множеств X и Y определяется следующим образом

ХY={ х: хХ и хY }.

Пример, Х = {0,2,3}, Y = {0,3,6,7}, ХY= {0, 3}.

Если X и Y не имеют общих элементов, то ХY = Ø. Из определения операции следует, что пересечение коммутативно ХY = YX - и ассоциативно (XY)Z = X(YZ). Это позволяет записывать без скобок также и пересечение множеств:

X₁X₂ ... X_n= {х: х  X₁ и х  X₂... и х  X_n}.

Операции объединения и пересечения связаны законами дистрибутивности

X (YZ) = (XY)  (XZ),

X (YZ) = (XY)  (XZ).

Разность множеств X и Y определяется следующим образом

X\Y={x: xX и xY}.

Пример. X = {0,2,7}, Y = {0,2,6,9}, X\Y = {7}.

Из определения разности следует, что (X\Y)  (XY) = X, т.к. для любого хX справедливо, что: либо хX, но xY, либо хX и хY.

Используя понятие разности множеств, при YX определим дополнение для Y во множестве X:

.

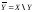Пример. Х= {1,3, 5,7, 8}, Y= {1,5, 7}, ={3,8}.

Используя операции объединения, пересечения и дополнения множеств, сформулируем законы Моргана:

Для количества элементов объединения нескольких множеств имеют место формулы включения-исключения. Вот некоторые из них:

|X₁X₂| = |X₁| + |X₂| - |X₁X₂|;

|X₁X₂X₃| = |X₁| + |X₂| + |X₃| - |X₁X₂| - |X₁X₃| - |X₃X₂| + |X₁X₂X₃|.

Семейство множеств {X₁, X₂, ..., X_k} называется покрытием множества X, если имеет место равенство X = X₁X₂ ... X_k. Множества X₁, X₂, ..., X_k называются блоками покрытия.

Важным примером покрытия является разбиение X. Семейство множеств {Х₁,Х_2,..., Х_k} называется разбиением множества X с блоками Х₁, Х₂,..., Х_k, если

X = X₁X₂ ... X_k, |X_i| >0, X_iX_j = Ø, ij, li,jk.

Пример. Множества {1, 2, 5}, {3, 2, 7} образуют покрытие множества {1, 2, 3, 5, 7}.

Множества {1, 4, 7}, {2, 3, 9}, {5, 6, 8} представляют собой блоки разбиения множества {1, 2, 3, 4, 5, 6, 7, 8, 9}.

Из определения разбиения следует, что порядок записи блоков, в силу коммутативности операции объединения множеств, может быть произвольным.

Для любого разбиения конечного множества

X = X₁X₂ ... X_k справедливо равенство

|X| = |X₁| + |X₂| +… + |X_k|.

Для покрытия конечного множества X = X₁X₂ ... X_k справедливо неравенство

|X|  |X₁| + |X₂| +… + |X_k|.

Совокупность всех упорядоченных пар (x,y) таких, что хХ, yY называется декартовым произведением множеств X и Y и обозначается X×Y.

X×Y={(x,y): хХ, yY}

Аналогично определяется декартово произведение k множеств X₁× X₂× ... × X_k ={( х₁, х₂,..., х_k): х₁Х₁, …., x_kX_k}, а при совпадении множеств - декартова степень X^(k) = X×X×…×X. Имеет место соотношение |X₁× X₂× ... × X_k |= |X₁|× |X₂|× ... × |X_k |

Рассмотрим некоторые примеры использования введённых здесь понятий: пересечения, объединения, разбиения.

Одним из основных методов решения задач на построение является метод геометрических мест. Если надо построить точку, удовлетворяющую двум условиям, то сначала сохраняют только одно из этих условий и опускают второе. Множество точек, удовлетворяющих первому условию, заполняет некоторую линию. Точно также множество точек, удовлетворяющих только второму условию, заполняет другую линию. Тогда искомая точка является пересечением этих двух линий. Например, пусть надо найти точку C, удаленную на расстояние R от точки O и равноудаленную от точек A и B. Искомая точка лежит на пересечении окружности радиуса R, с центром в O с перпендикуляром к отрезку AB, проходящему через его середину.

Множество всех квадратов является пересечением множества всех прямоугольников с множеством всех ромбов.

Решение систем уравнений и неравенств, по сути дела, сводится к отысканию пересечения множеств, являющихся решениями каждого уравнения или неравенства в отдельности.

Весьма часто в различных предметных областях используется понятие разбиения множества на подмножества. Наиболее часто его используют при различного рода классификациях объектов.

При составлении каталога книг в библиотеке все множество книг разбивают на книги беллетристического характера, книги по общественно-политическим наукам, по естественным наукам, математике, экономике и т.д. При составлении алфавитного каталога, сначала книги разбиваются на подмножество книг, фамилии авторов которых начинаются на А, подмножество книг, фамилии авторов которых начинаются на Б, и т.д.

Часто разбиение множества на подмножества (эти подмножества в практической жизни часто называют классами) производится путем указания некоторого отношения (обозначим это отношение буквой ) между каждой парой элементов объединяемых в один класс. Однако не всякое отношение между элементами приводит к желаемому разбиению. Например, для множества людей отношение «быть знакомыми» не может привести к разбиению. Если х знаком с у (xy), а у знаком с z (yz), это вовсе не означает, что х знаком с z. Так как нам придётся сначала отнести в один класс х и у (они знакомы друг с другом), потом в этот же класс включить и z (он знаком с у), тогда в одном классе окажутся незнакомые друг с другом х и z. Чтобы не возникало подобных ситуаций, нужно, чтобы отношения между элементами множества удовлетворяли ряду условий:

Каждый элемент х сам с собой находится в отношении , то есть хх. Это свойство называется - рефлексивность);

если элемент х находится в отношении  с элементом у, то элемент у находится в отношении  с элементом х. То есть, из xy следует ух. Это свойство называется симметричность;

если элемент х находится в отношении  с элементом у, а у находится в отношении  с элементом z, то элемент х находится в отношении  с элементом z. То есть, из xy и уz следует xz. Это свойство транзитивности.

Отношения, удовлетворяющие этим свойствам, называются отношениями эквивалентности.

Можно доказать, что выполнение этих условий необходимо и достаточно для того, чтобы множество можно было разбить на классы эквивалентных между собой элементов, и при том так, что разные классы не имеют общих элементов.

Рассмотрим специально один из случаев разбиения множества целых чисел.