4.2. Вычисление ранга матрицы

Вычисление ранга матрицы можно проводить одним из следующих способов.

Первый состоит в сведении данной матрицы с помощью элементарных преобразований к канонической матрице. Каноническая матрица является блочной матрицей, у которой один из блоков представляет собой единичную матрицу, а все остальные блоки – нулевые матрицы.

Каноническую матрицу можно записать в виде

.

Ранг канонической матрицы равен, очевидно, числу единиц, стоящих на диагонали. Преобразования, не меняющие ранга матрицы, называются элементарными. К их числу относятся:

1. Перестановка двух любых столбцов (строк) матрицы.

2. Умножение столбца (строки) на отличное от нуля число.

3. Прибавление к одному столбцу (строке) линейной комбинации других столбцов (строк).

Пример. Вычислить ранг матрицы

.

Вычтем первый столбец из четвертого и шестого, а в получившейся матрице второй столбец прибавим к четвертому, вычтем его из шестого, и удвоенный второй столбец вычтем из пятого:

.

В полученной матрице третий столбец прибавим к пятому и вычтем из четвертого

.

Далее, четвертый столбец прибавим к третьему, удвоенный четвертый столбец прибавим к пятому и шестому. Наконец, в полученной матрице вычтем третий столбец из второго, а получившийся второй из первого

.

Ранг последней матрицы равен, очевидно, 4.

Второй способ вычисления матрицы дает метод окаймления миноров, основанный на следующей теореме:

Теорема. Пусть матрица имеет минор го порядка отличный от нуля, а все миноры го порядка, содержащие (окаймляющие) его равны нулю. Тогда ранг матрицы равен .

Пример. Вычислить ранг матрицы методом окаймления миноров

.

У матрицы имеется минор второго порядка . Поэтому ранг данной матрицы не меньше двух. Окаймляют данный минор следующие миноры третьего порядка

.

Так как все они равны нулю, ранг матрицы равен двум.

4.3. Задачи

Вычислить ранг следующих матриц методом окаймления миноров.

1. . 2. .

Вычислить ранг следующих матриц при помощи элементарных преобразований.

3. . 4. .

5. Чему равен ранг матрицы

при различных значениях ?

6. Доказать, что система вектор – столбцов, содержащая нулевой вектор, линейно зависима.

7. Доказать, что если часть системы вектор – столбцов линейно зависима, то и вся система линейно зависима.

8. Найти все значения , при которых вектор – столбец линейно выражается через вектор – столбцы .

а) .

б) .

5. Системы линейных уравнений

5.1. Основные определения

Определение 1. Системой линейных уравнений относительно неизвестных называется система уравнений вида

где произвольные заданные числа – коэффициенты уравнений, свободные члены.

Если ввести матрицы

,

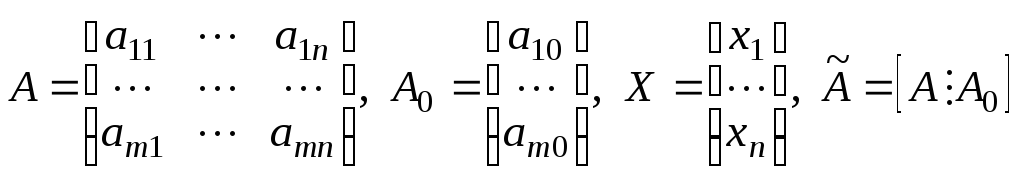то систему уравнений можно записать в матричном виде

.

Матрица называется основной матрицей системы, матрица расширенной матрицей системы.

Если , то система называется квадратной. Если все , система называется однородной.

Определение 2. Решением системы линейных уравнений называется всякая совокупность чисел , которая при подстановке в систему вместо неизвестных превращает систему уравнений в систему тождеств. Система, имеющая хотя бы одно решение, называется совместной (разрешимой).

Определение 3. Всякое решение совместной системы называется ее частным решением. Совокупность всех частных решений называется общим решением.

Определение 4. Две системы уравнений называются эквивалентными, если каждое решение одной системы является решением другой.

В следующей теореме формулируется условие совместности системы линейных уравнений.

Теорема Кронекера – Копелли. Система линейных уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы этой системы.

Теорема (о числе решений совместной системы). Всякая совместная система уравнений с неизвестными ранга при имеет единственное решение. Если , то система имеет бесконечно много решений.

Выделим в основной матрице совместной системы базисный минор.

Определение 5. Уравнения системы, соответствующие базисным строкам матрицы, называются базисными уравнениями. Их совокупность называется базисной системой уравнений. Неизвестные, коэффициенты при которых образуют базисные столбцы матрицы системы, называются главными неизвестными, остальные – свободными.

Всякая линейная система эквивалентна системе своих базисных уравнений.

При решении линейной системы, прежде всего, выделяют базисную систему. Если базисная система является совместной и состоит из уравнений с неизвестными, то далее главных неизвестных выражают через свободных.