
- •Матрицы. Системы линейных уравнений
- •1. Матрицы
- •1.1. Основные понятия
- •1.2. Действия с матрицами
- •1.3. Задачи
- •2. Определители
- •2.1. Основные понятия
- •2.2. Свойства определителя
- •2.3. Алгебраические дополнения. Миноры. Формулы разложения определителя по столбцу или строке
- •2.4. Вычисление определителей
- •2.5. Задачи
- •3. Обратная матрица
- •3.1. Задачи
- •4. Ранг матрицы
- •4.1. Основные понятия
- •4.2. Вычисление ранга матрицы
- •4.3. Задачи
- •5. Системы линейных уравнений
- •5.1. Основные определения
- •5.2. Квадратные системы. Формулы Крамера
- •5.3. Метод Гаусса
- •5.4. Задачи
- •6. Однородные линейные системы
- •6.1. Общее решение однородной системы
- •6.2. Задачи
- •7. Неоднородные системы
- •7.1. Общее решение неоднородной системы
- •7.2. Задачи
- •Литература
1.3. Задачи
Вычислить произведения матриц:
1.
![]() 2.
2.
![]() .
3.
.
3.
![]() .
.
4.
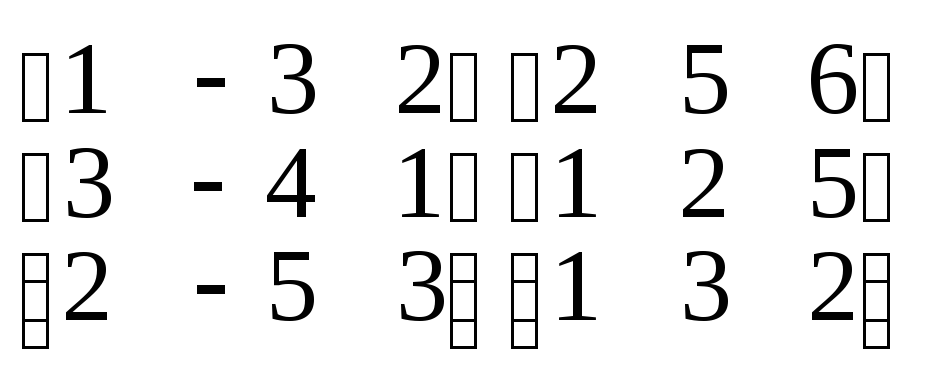 .
5.
.
5.
![]() .
.
6. Доказать, что если для матриц
![]() и
и
![]() оба произведения
оба произведения
![]() и
и
![]() существуют, причем
существуют, причем
![]() ,
то матрицы
,
то матрицы
![]() и
и
![]() - квадратные и имеют одинаковый порядок.
- квадратные и имеют одинаковый порядок.
Вычислить выражения:
7.
![]() .
8.
.
8.
![]() .
9.
.
9.
![]() .
.
10.
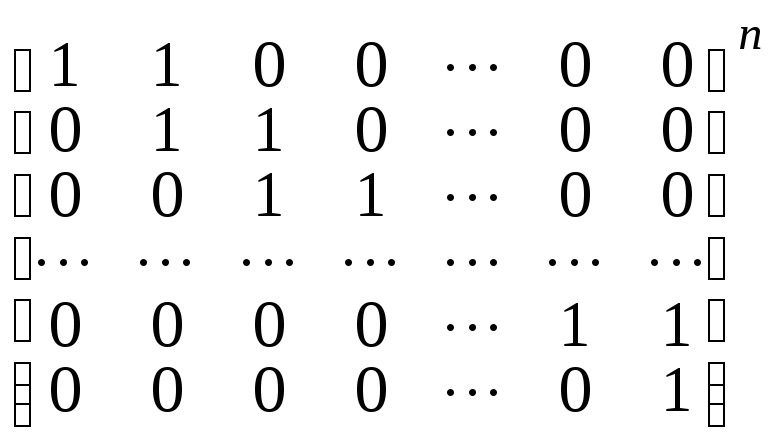 ,
порядок матрицы равен
,
порядок матрицы равен
![]() .
.
11. Найти значение многочлена
![]() от матрицы
от матрицы
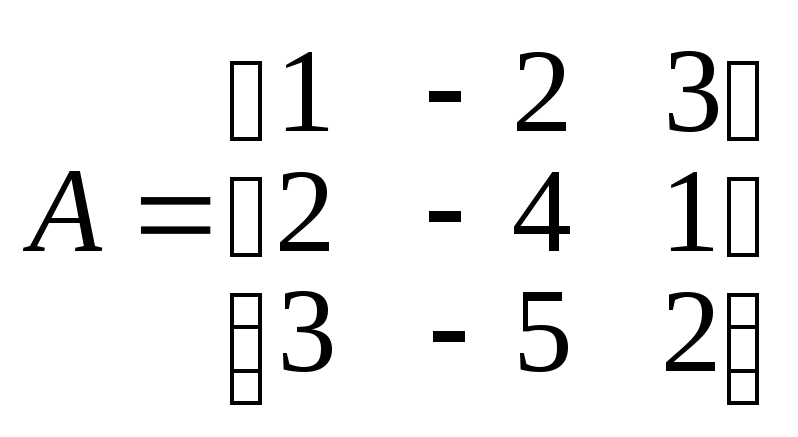 .
.
12. Доказать, что если матрицы
![]() и
и
![]() - квадратные и имеют одинаковый порядок,
причем
- квадратные и имеют одинаковый порядок,
причем
![]() ,
то
,
то
а)
![]() .
б)
.
б)
![]() .
.
13. Доказать, что если матрицы
![]() и
и
![]() - квадратные и имеют одинаковый порядок,
причем
- квадратные и имеют одинаковый порядок,
причем
![]() ,
то
,
то
![]() .
.
14. Найти все матрицы, перестановочные с матрицей
![]() .
.
2. Определители
2.1. Основные понятия
Понятие определителя вводится только
для квадратных матриц. Пусть
![]() — квадратная матрица порядка
— квадратная матрица порядка![]() .
Составим произведение из
.
Составим произведение из
![]() различных элементов матрицы
различных элементов матрицы
![]() ,
выбирая по одному и только одному
элементу из каждой строки и каждого
столбца. Запишем это произведение в
виде
,
выбирая по одному и только одному
элементу из каждой строки и каждого
столбца. Запишем это произведение в
виде![]() .
Будем называть его членом определителя.
Рассмотрим последовательность чисел
.
Будем называть его членом определителя.
Рассмотрим последовательность чисел
![]() .
По самому построению члена определителя
это различные числа, которые представляют
собой перестановку чисел от 1 до
.
По самому построению члена определителя
это различные числа, которые представляют
собой перестановку чисел от 1 до
![]() .
Назовем инверсией в перестановке
.
Назовем инверсией в перестановке
![]() такое расположение чисел, когда старшее
стоит перед младшим. Например, в
перестановке 1,2,4,5,7,9,10,8,3,6 будет 12 инверсий.
Обозначим число инверсий в перестановке
через
такое расположение чисел, когда старшее
стоит перед младшим. Например, в
перестановке 1,2,4,5,7,9,10,8,3,6 будет 12 инверсий.
Обозначим число инверсий в перестановке
через
![]() .
Так как из
.
Так как из
![]() чисел можно составить
чисел можно составить
![]() различных перестановок, то число
различных членов определителя равно
различных перестановок, то число
различных членов определителя равно
![]() !
!
Определение. Определителем
(детерминантом) матрицы
![]() называется алгебраическая сумма
называется алгебраическая сумма
![]() !
членов определителя перед каждым из
которых стоит знак
!
членов определителя перед каждым из
которых стоит знак
![]() .
Или
.
Или
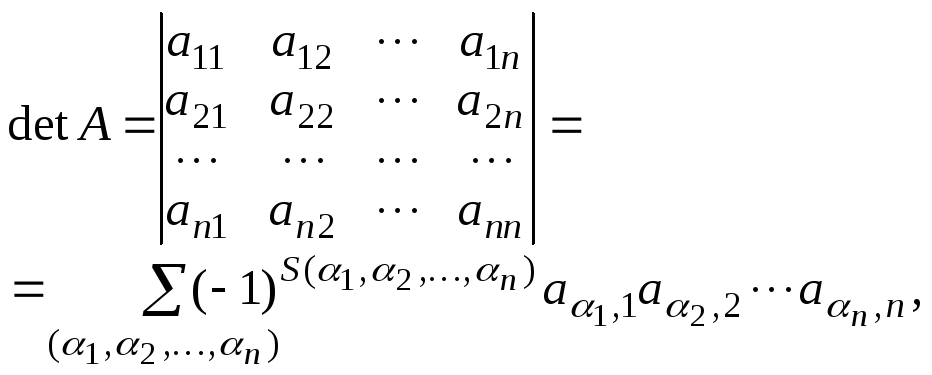
где сумма берется по всем возможным
перестановкам
![]() .
.
Хотя определитель матрицы это число,
будем для удобства столбцы и строки
матрицы
![]() называть также столбцами и строками ее
определителя
называть также столбцами и строками ее
определителя
![]() .
.
Пример. Вычислим определитель матрицы второго порядка
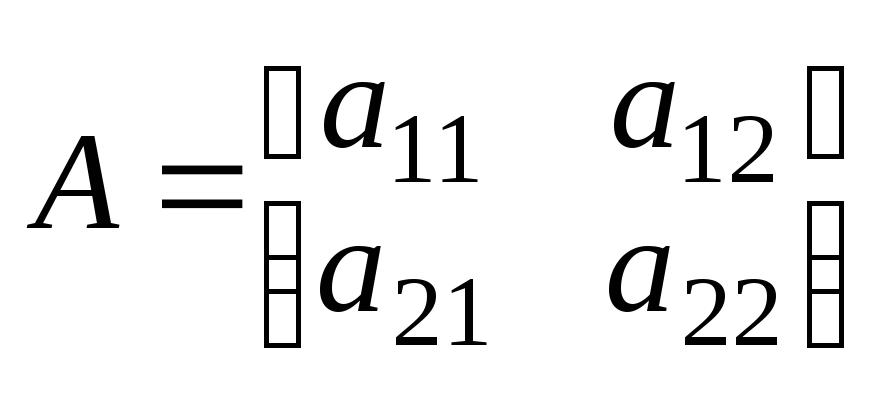 .
.
Члены определителя имеют вид
![]() ,
где
,
где
![]() принимают значения 1 и 2. Возможны две
пары значений
принимают значения 1 и 2. Возможны две
пары значений
![]() и
и
![]() .
Поэтому
.
Поэтому
![]() .
.
2.2. Свойства определителя
1. При транспонировании матрицы ее
определитель не меняется, т.е.
![]() .
Поэтому свойства, сформулированные для
столбцов матрицы, справедливы и для
строк.
.
Поэтому свойства, сформулированные для
столбцов матрицы, справедливы и для
строк.
2. При перестановке двух столбцов (строк) матрицы ее определитель меняет знак на противоположный.
3. Обозначим через
![]() определитель,
определитель,
![]() й
столбец которого есть вектор-столбец
й
столбец которого есть вектор-столбец
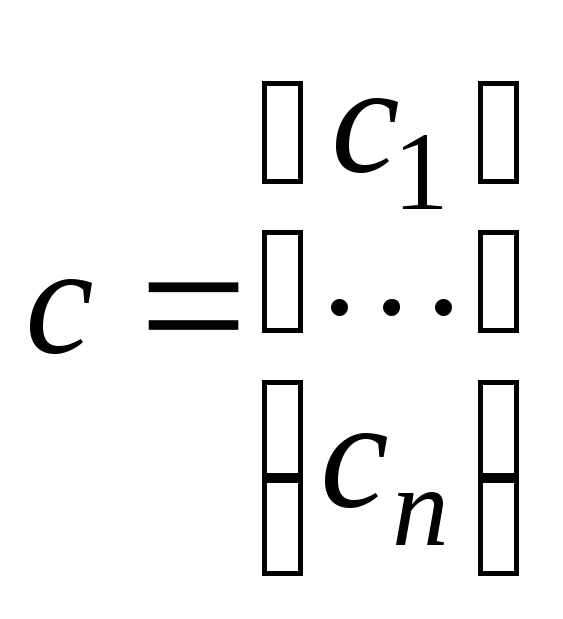 .
Если все элементы
.
Если все элементы
![]() го
столбца определителя представлены в
виде линейной комбинации двух слагаемых
го
столбца определителя представлены в
виде линейной комбинации двух слагаемых
![]() ,
где
,
где
![]() и
и
![]() фиксированные числа, то определитель
равен линейной комбинации двух
определителей
фиксированные числа, то определитель
равен линейной комбинации двух
определителей
![]() .
.
Например,
![]() .
.
4. Определитель матрицы с двумя одинаковыми столбцами равен нулю.
6. Если некоторый столбец матрицы состоит из нулей, то определитель этой матрицы равен нулю.
7. Если к элементам одного столбца определителя прибавить соответствующие элементы другого столбца, умноженные на одно и то же число, то определитель не изменится. Например,
![]() .
.
2.3. Алгебраические дополнения. Миноры. Формулы разложения определителя по столбцу или строке
Рассмотрим определитель матрицы
![]() .
.
Выделим в этом определителе произвольный
элемент
![]() ,
соберем в правой части равенства все
члены определителя, в которые входит
,
соберем в правой части равенства все
члены определителя, в которые входит
![]() ,
и вынесем этот элемент за скобки. Величина
,
и вынесем этот элемент за скобки. Величина
![]() ,
стоящая в скобках, называется алгебраическим
дополнением элемента
,
стоящая в скобках, называется алгебраическим
дополнением элемента![]() в определителе
в определителе
![]() .
.
Например, в определителе третьего
порядка алгебраическое дополнение
элемента
![]() ,
а элемента
,
а элемента
![]() .
.
Так как в каждый член определителя
входит один и только один элемент
![]() го
столбца, то можно записать, что
го
столбца, то можно записать, что
![]() .
.
Это соотношение называется формулой
разложения определителя по элементам![]() го
столбца. Аналогичная формула
записывается и для любой
го
столбца. Аналогичная формула
записывается и для любой
![]() й
строки
й
строки
![]() .
.
Рассмотрим теперь квадратную матрицу
![]() го
порядка
го
порядка

Выделим в этой матрице произвольные
![]() строк с номерами
строк с номерами
![]() и столько же столбцов с номерами
и столько же столбцов с номерами
![]() .Элементы,
стоящие на пересечении выбранных строк
и столбцов образуют квадратную матрицу
.Элементы,
стоящие на пересечении выбранных строк
и столбцов образуют квадратную матрицу
![]() го
порядка. Ее определитель называется
минором
го
порядка. Ее определитель называется
минором
![]() го
порядка матрицы
го
порядка матрицы
![]() и обозначается
и обозначается
![]() .
Всякий элемент по определению есть
минор 1-го порядка, а
.
Всякий элемент по определению есть
минор 1-го порядка, а
![]() есть минор
есть минор
![]() го
порядка.
го
порядка.
Если в исходной матрице зачеркнуть
![]() строк с номерами
строк с номерами
![]() и
и
![]() столбцов с номерами
столбцов с номерами
![]() ,
то оставшиеся элементы образуют
квадратную матрицу порядка
,
то оставшиеся элементы образуют
квадратную матрицу порядка
![]() .Определитель
этой матрицы
.Определитель
этой матрицы
![]() называется дополнительным минором
для минора
называется дополнительным минором
для минора
![]() .
Дополнительный минор к элементу
.
Дополнительный минор к элементу
![]() обозначается
обозначается
![]() .
.
Например, в матрице
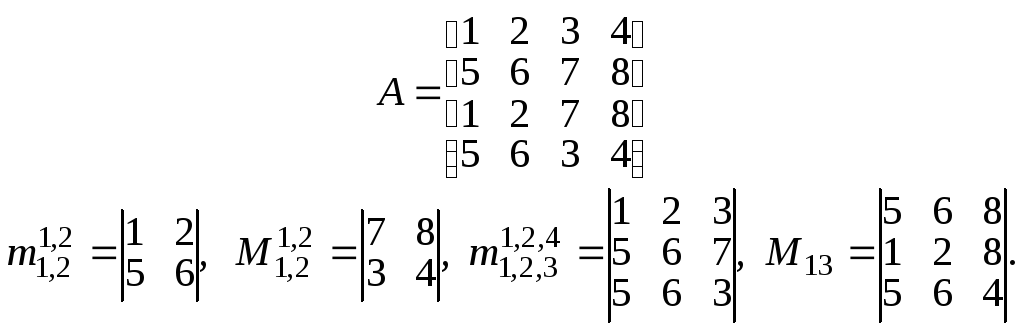
Миноры
![]() и алгебраические дополнения
и алгебраические дополнения
![]() связаны между собой следующим равенством:
связаны между собой следующим равенством:
![]() Из формул разложения определителя по
строке или столбцу получаем, что
Из формул разложения определителя по
строке или столбцу получаем, что
![]() .
.
Обобщением этих формул является теорема
Лапласа. Пусть в определителе
![]()
![]() го
порядка выделены любые
го
порядка выделены любые
![]() столбцов с номерами
столбцов с номерами
![]() .
Составим всевозможные миноры
.
Составим всевозможные миноры
![]() го
порядка из элементов, находящихся на
пересечении этих столбцов и произвольных
го
порядка из элементов, находящихся на
пересечении этих столбцов и произвольных
![]() строк определителя с номерами
строк определителя с номерами
![]() (
(![]() ).
Тогда
).
Тогда
![]() ,
,
где
![]() .
Аналогичное разложение можно записать
и для произвольных
.
Аналогичное разложение можно записать
и для произвольных
![]() строк определителя
строк определителя
![]() .
.
