Плоскость

Общее уравнение плоскости a*Px+b*Py+c*Pz+d=0 или или . Параметрически задается в виде , где L1,L2 – два непараллельных вектора в плоскости.

Расстояния от точки до плоскости .

Прямая

Уравнение прямой, проходящей, через две точки.

Является также пересечением двух плоскостей, и может быть задана в виде системы из двух уравнений плоскости , либо параметрически .

Получить направление и точку для параметрического задания можно следующим образом (должен лежать в обеих плоскостях, а значит – быть перпендикулярным обеим нормалям). А точку получить из пересечения трех плоскостей, двух исходных и третьей – с нормалью L и проходящей через начало координат. Получаем систему

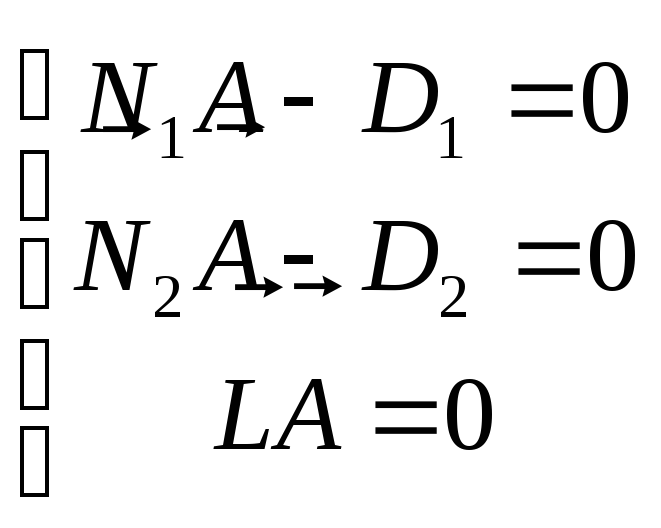, ее решением будет .

В конце имеет смысл нормализовать вектор L.

Расстояния от точки до прямой .

Р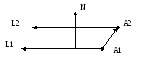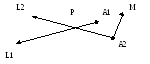асстояние между прямыми считается следующим образом, сначала находится направление, перпендикулярное обеим прямым , а затем уже само расстояние, как проекция вектора A1A2 на это направление . Если же прямые параллельны (), то расстояние считается как расстояние от точки одной прямой до другой, например, . Если расстояние равно нулю – прямые пересекаются (при параллельных прямых – коллинеарны).

Две наиболее близкие точки прямых, проецируются в ту же точку, что и точка пересечения проекций прямых на плоскость с нормалью N. Поэтому можно воспользоваться формулами пересечения прямых для плоского случая. При этом плоскость задана базисом (L2,M) M=L2xN.

,

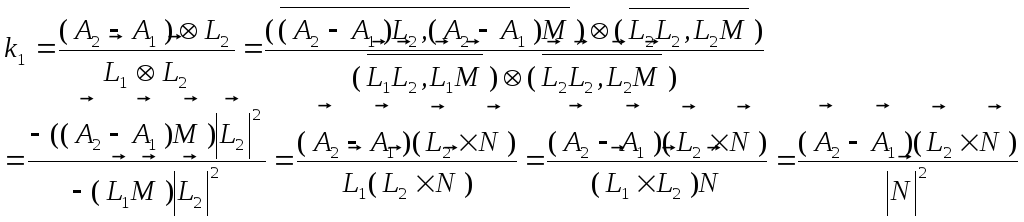
Пересечение прямой с плоскостью . , .

Сфера

Общее уравнение , или

Практически все формулы остаются как у окружности.

Полигон

Это тот же полигон, только плоскость, в которой он лежит имеет некоторую ориентацию в пространстве. Т.о. сохраняются все свойства и алгоритмы для полигона на плоскости. Нормаль к плоскости в которой лежит треугольник ABC . Нормаль к плоскости в которой лежит произвольный полигон можно получить, либо взяв три неколлинеарные вершины, либо по формуле Ньэла.

,

Конечно затем нужно нормализовать N.

Более простая формула Ньэла .

Все алгоритмы для 2D случая можно применять и в 3D, это можно делать тремя способами:

1. Совместить плоскость полигона с плоскостью OXY и далее работать как в 2D случае.

2. Работать с проекциями полигона (правда, в проекциях нельзя правильно посчитать площадь) на одну из ортогональных плоскостей OXY, OXZ, OYZ. Плоскость выбирается в зависимости от нормали (например, если максимальным является модуль компоненты z выбирается плоскость OXY).

3. Работать в 3D пространстве с некоторыми модификациями формул. В основном это касается pdp, оно заменяется на смешанное произведение .

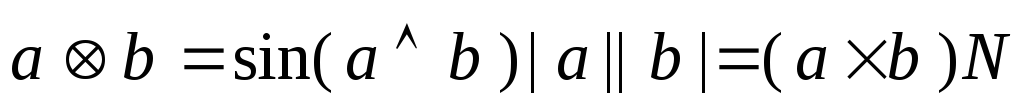Отсечение отрезка и полигона плоскостью

В 3D отсечение обычно выполняют по алгоритму по Кируса-Бэка, только расстояния от вершин отрезков до прямой заменяются на расстояния до плоскости. В остальном, все происходит тем же образом, что и на плоскости.

Полиэдр (многогранник)

Обычно под словом полиэдр (polyhedron) понимают выпуклые многогранники. Многогранник состоит из вершин, ребер и граней. Самый простой полиэдр – тетраэдр. Выпуклый – это значит, что все точки полиэдра находятся с одной стороны от плоскостей, образующих его грани (обычно с отрицательной стороны, так, что нормали плоскостей смотрят наружу). Наиболее часто полиэдры задаются просто набором ограничивающих плоскостей. Но полиэдр можно задать и набором полигонов – граней полиэдра, но это избыточное задание. Если полиэдр задан набором плоскостей, то получить его грани можно отсечением. Обычно создается начальный достаточно большой полигон в плоскости, для которой требуется получить грань, а затем отсекается всеми остальными плоскостями полиэдра. Можно поступить иначе – найти все прямые, по которым текущая плоскость пересекается с остальными, а затем отсечь их по оставшимся плоскостям, т.о. получатся ребра грани останется только объединить их в полигон (здесь правда могут возникнуть сложности с близкими точками).

Положение точки относительно полиэдра

Чтобы определить, находится ли точка внутри полиэдра или снаружи нужно посчитать расстояния от точки до каждой плоскости полиэдра, и если точка находится под всеми плоскостями (все расстояния отрицательны), значит она внутри.

Объем полиэдра

Объем тетраэдра

Объем полиэдра – сумма объемов тетраэдров, построенных на начале координат и треугольниках на гранях полиэдра.

Булевы операции с полиэдрами

Это операции над множествами точек, внутри полиэдров. Операция «И» (получение пересечения (общей части) двух полиэдров), «ИЛИ» (объединение двух полиэдров), «НЕ-И» (вычитание одного полиэдра из другого). Они используются при работе с конструктивной геометрией (Constructive solid geometry).

Общую часть двух полиэдров («И») можно получить путем отсечения одного полиэдра плоскостями другого, в результате получается выпуклый полиэдр. Общий полигон обычно получают следующим образом, сначала записывают в список его плоскостей все плоскости обоих полиэдров, потом находят грани для такого полиэдра, и выбрасывают из набора плоскостей те, которым соответствуют пустые грани.

В результате вычитания одного полиэдра h1 из другого h2 («НЕ-И») получается набор полиэдров. Обычно поступают следующим образом, находят грань h1, которая находится внутри h2 (отсекают грань h1 плоскостями полиэдра h2) и разделяют h1 плоскостью этой грани, полиэдр с положительной стороны записывают в выходной набор, а с оставшуюся часть продолжают делить остальными плоскостями. В случае, если нет ни одной грани h1 внутри h2, полиэдры либо не пересекаются (операция «И» дает пустой полиэдр), тогда результатом является h1, либо h2 целиком находится внутри h2, тогда результатом является пустой набор полиэдров.

Объединение двух полиэдров («ИЛИ») это один из них и результат вычитания его из второго. В особых случаях, когда один полиэдр лежит внутри другого (все вершины одного внутри или на границе другого) имеет смысл просто оставить больший полиэдр.