Лекция 4,5 Преобразования на плоскости и в пространстве

В компьютерной графике все что относится к плоскому случаю принято обозначать 2D (2-dimentional) двумерное, а все что относится к пространственным – 3D.

Аффинные преобразования на плоскости

Affinis – родственный (лат). Потому, что фигуры сохраняются при аффинных преобразованиях.

Предположим, существует некоторая прямолинейная система координат (OXY). Тогда, каждой точке М можно поставить в соответствие пару координат (x,y). Введя другую систему координат O^*X^*Y^*, можно поставить той же точке М другую пару координат (x^*,y^*). Переход от одной системы к другой:

x^*=ax+by+c, с условием |a b|0

y^*=dx+ey+f |d e|

Эти формулы можно рассматривать двояко, либо сохраняется точка, и изменяется система координат, либо сохраняется система координат и изменяется точка. В дальнейшем эти формулы будут рассматриваться именно как преобразование точек в заданной системе координат. Причем все рассматриваемые системы будут прямоугольными (формулы позволяют работать и с непрямоугольными).

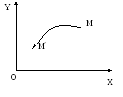
Нужно отметить, что координаты точки M можно представить в виде вектораиз начала координат с координатами Mx,My.

Тогда преобразование можно записать в векторной форме (это справедливо только для прямоугольной системы координат).

M*=((M-O*)X*,(M-O*)Y*)

, где O*-координаты начала координат второй системы в координатах первой. X*,Y* - орты (направляющие вектора) второй системы координат в координатах первой.

a=(Xx*), b=(Xy*),c=-O*X*

d=(Yx*), e=(Yy*),f=-O*Y*

Это преобразование можно записать и в матричном виде

, или 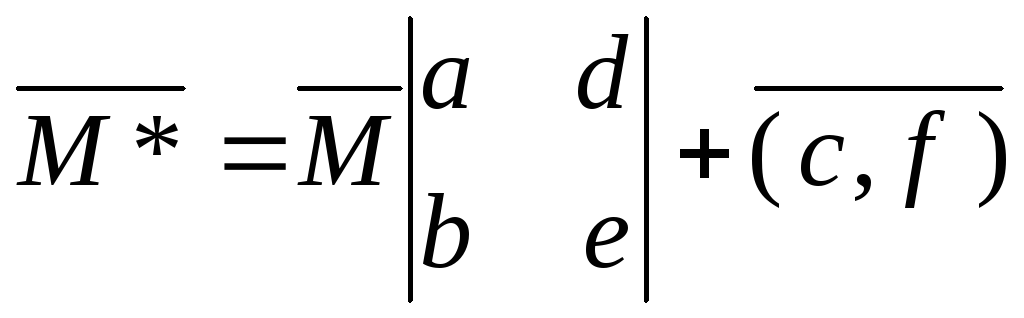, где вектора считаются в виде матриц вида 12.

Элемент Cij матрицы C=AB есть сумма произведений элементов i-ой строки матрицы A на элементы j-ого столбца матрицы B.

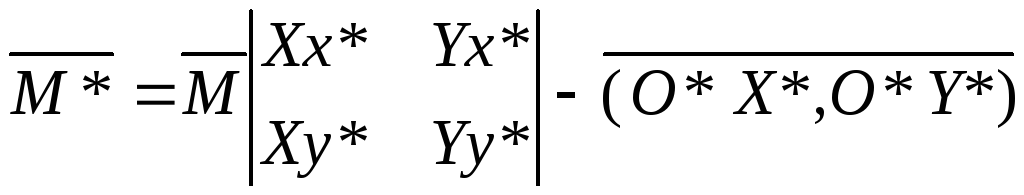
Обратное преобразование – решение системы линейных уравнений, либо использовать обратную матрицу 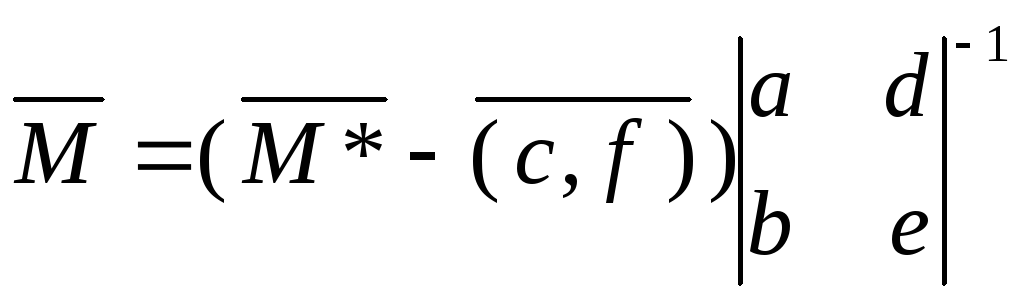, но для случая, когда система представлена ортами можно проще. С этом случае обратная матрица равна транспонированной.

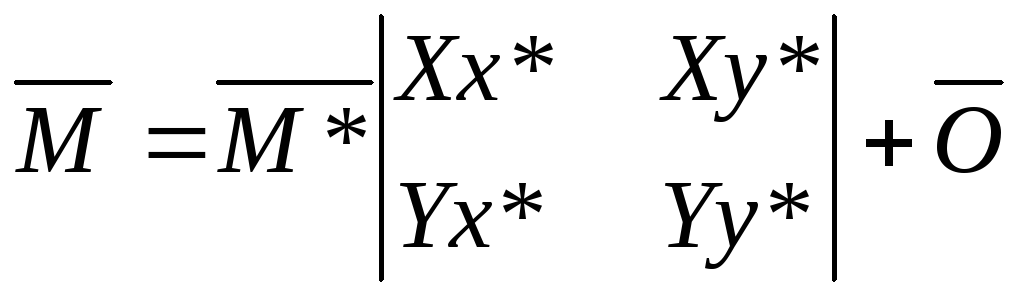
Аффинное преобразование – геометрическое преобразование плоскости или пространства которое можно получить комбинируя поворот, перенос, зеркальные отражения и масштабирование в направлениях координатных осей.

Поворот (R - rotation). Вокруг начала координат на угол .

x^*=x*cos-y*sin

y^*=x*sin+y*cos

Растяжение, сжатие вдоль координатных осей (D – dilatation).

x^*=k*x

y^*=m*y

k>0, m>0

Отражение (M – mirror). Относительно оси абсцисс.

x^*=x

y^*=-y

Перенос (T – translation).

x^*=x+a

y^*=y+b

Перенос представить в виде произведений вектора на матрицу нельзя, зато можно в виде суммы векторов.

В курсе аналитической геометрии доказывается, что любое преобразование можно представить как последовательное исполнение (суперпозицию) этих простейших преобразований.

Иногда удобно представлять все преобразования в одной матричной форме, для этого используют однородные координаты.

Однородные координаты

Для точки M с координатами x,y на плоскости, однородными координатами является тройка чисел x1,x2,x3, одновременно неравная нулю и связанная соотношениями x1/x3=x, x2/x3=y. Точке с координатами x,y на плоскости сопоставляется точка xh,y,h,h в однородном пространстве, обычно h=1 (x,y,1).

Общее преобразование точек в однородных координатах можно записать в виде.

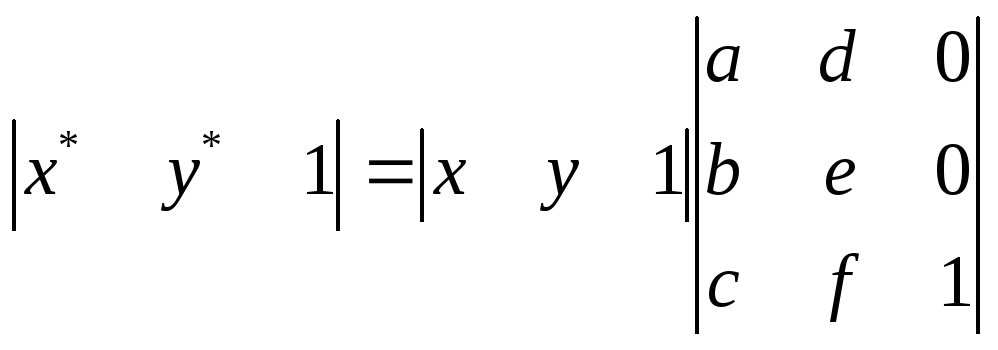
А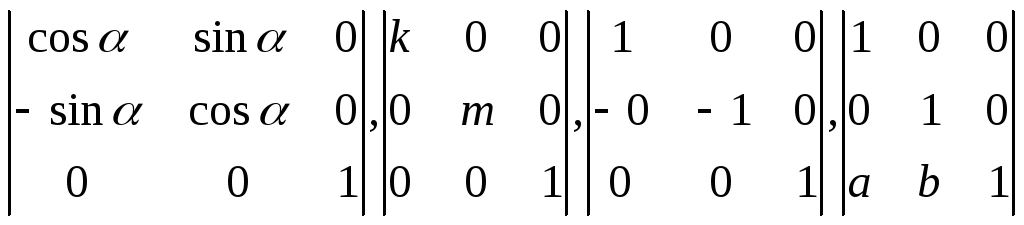 матрицы основных преобразований будут выглядеть следующим образом:

[R] [D] [M] [T]

Комбинация преобразований.

Предположим нужно повернуть точку на угол вокруг некоторой точки A.

Н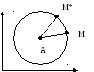ачала переносим точку A в начало координат (-Ax,-Ay). Затем поворот. Затем перенос обратно в точку А. (Ax,Ay). Можно получить единое преобразование [T(-A)][R(a)][T(A)]

Аффинные преобразования в пространстве

В 3D пространстве точка (вектор) представляется тремя координатами (x,y,z), или четырьмя однородными координатами (x,y,z,1).

Следует ввести понятия левая и правая тройка векторов. Три вектора a,b,c образуют правую тройку, если после совмещения начал векторов кратчайший поворот от a к b кажется наблюдателю, смотрящему с конца вектора c идущим против часовой стрелки. Правило правой руки – вектор a совмещается с локтем, вектор b входит в ладонь, вектор c совпадает с большим пальцем. Система координат называется правой, если ее направляющие вектора образуют правую тройку.

Векторное произведение c=ab, с – вектор перпендикулярный обоим векторам, образует с ними правую тройку.

Cx=Ay*Bz-Az*By, Cy=Az*Bx-Ax*Bz, Cz=Ax*By- Ay*Bx

Преобразования остаются те же: вращение (только теперь вокруг трех осей), растяжение, отражение (относительно трех плоскостей), перенос.

Вращение против часовой, если смотреть из начала координат для левой системы координат (для правой – наоборот).

, ,

,

, ,

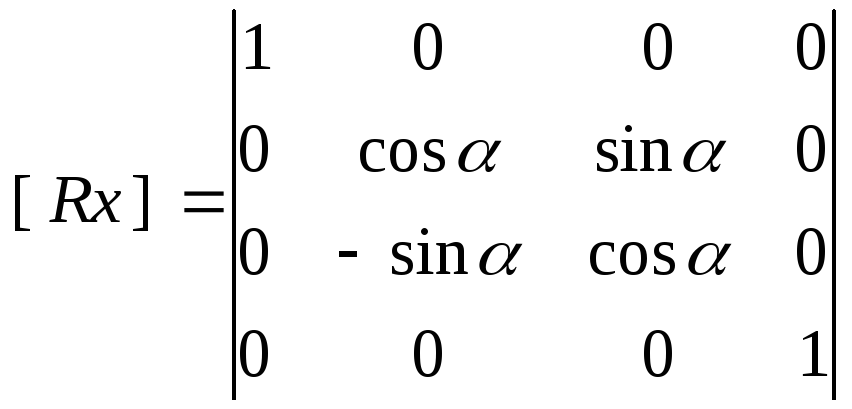
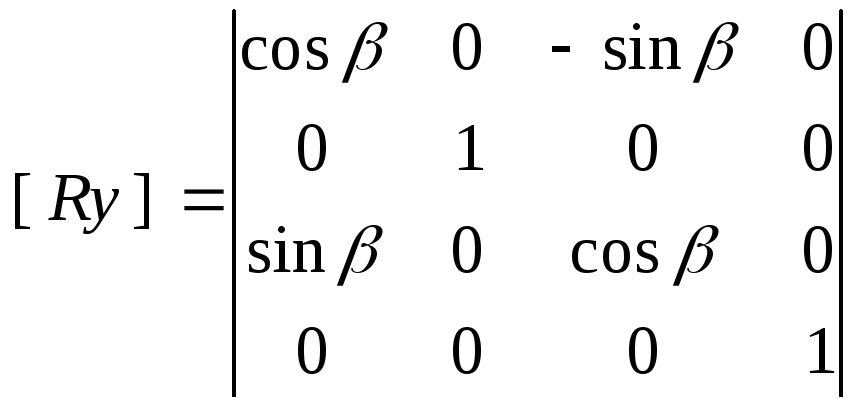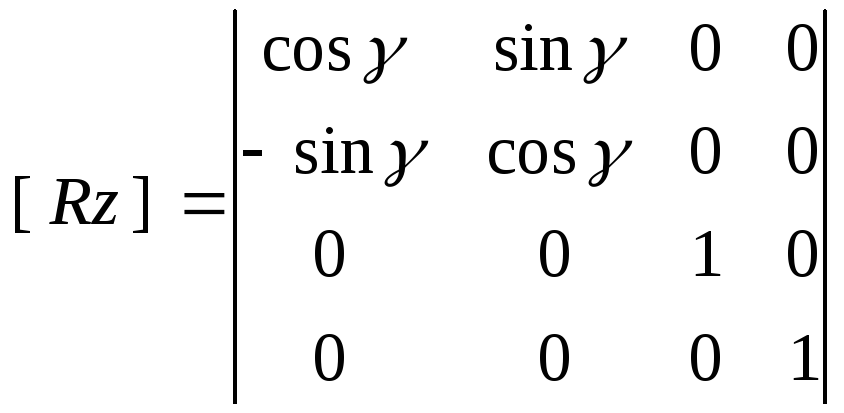
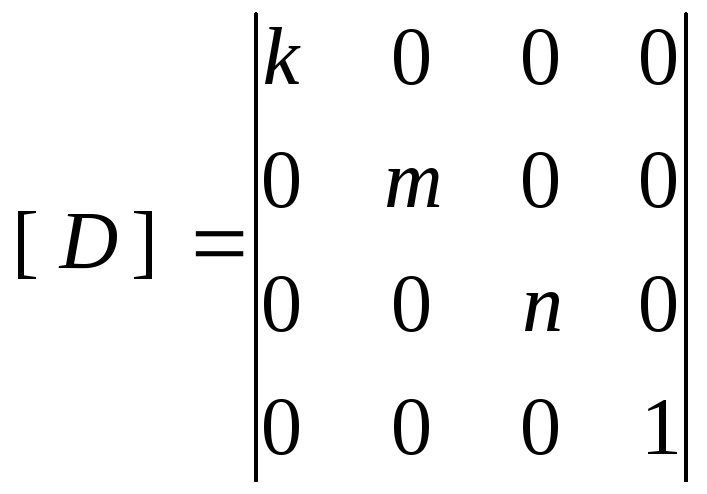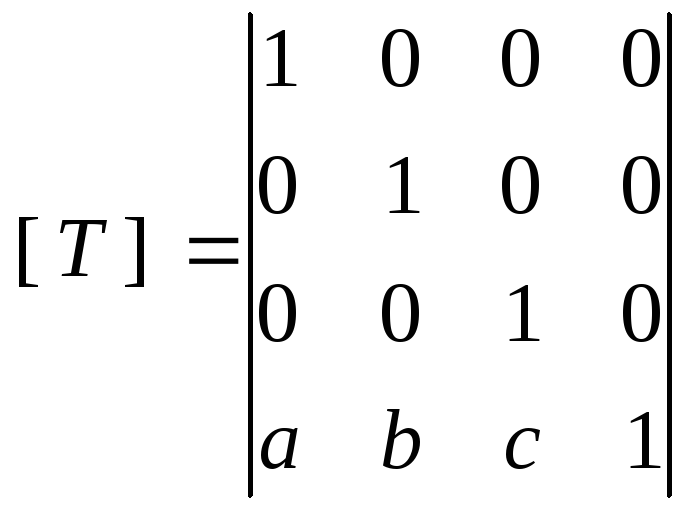
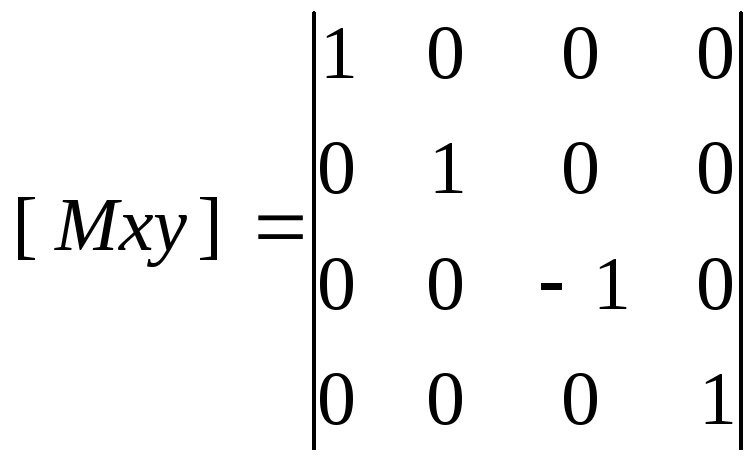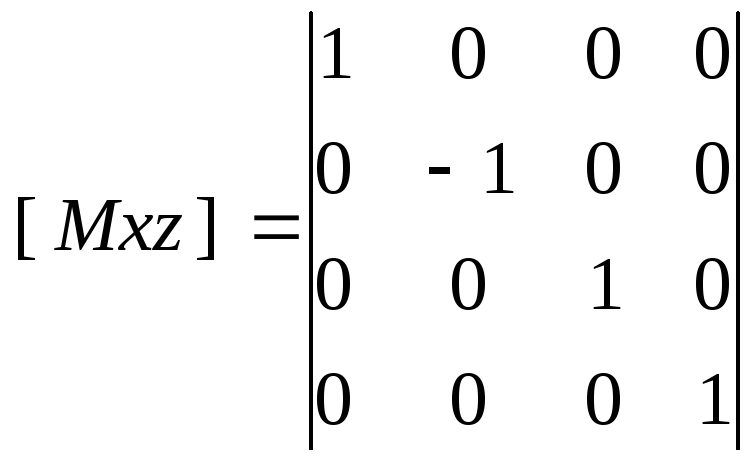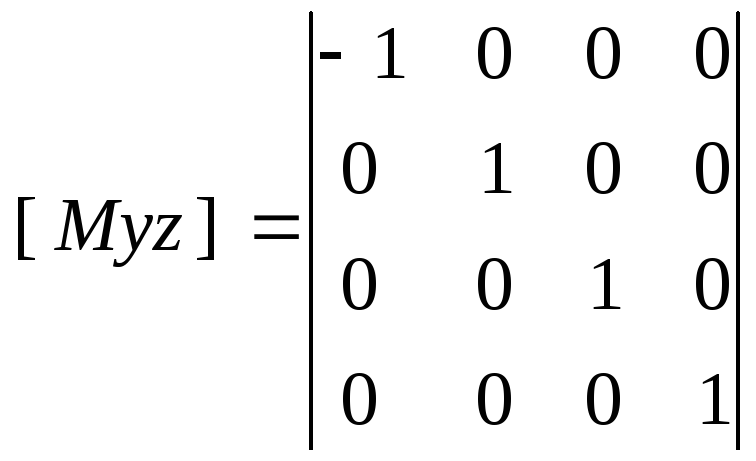
Например, нужно построить матрицу вращения относительно прямой с направляющим ортом L, проходящей через точку A.

1. Перенос A в начало координат [T(-A)]

2. Совмещение прямой с осью X.

Сначала поворот вокруг оси X

на угол  [Rx()], cos=Lz/d, sin=Lx/d, где d=

Если d=0, значит прямая уже совпадает с осью X.

Затем поворот вокруг оси Y на угол  [Ry()].

Повернутый вектор равен (Lx,Ly,Lz,1)[Rx]=(Lx,0,d,1).

cos=Lx, sin=d

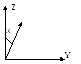
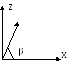
3. Поворот вокруг оси X на нужный угол [Rx()]

4. Возвращение к оси L [Ry(-)],[Rx(-)]

5. Перенос на точку A [T(A)]

Общая матрицы получится

[T(-A)] [Rx()][Ry()][Rx()][Ry(-)][Rx(-)][T(A)]

Преобразование в систему координат заданную ортами

Если система задана тройкой взаимно перпендикулярных ортов X*,Y*,Z*.

, обратное преобразование – транспонированная матрица [R]^T

Проектирование

Проектирование необходимо в первую очередь, для того, чтобы отобразить трехмерные объекты на плоском экране, но существуют и другие применения, например, тени.

Существует два наиболее употребляемых вида проектирования параллельное и центральное (перспективное).

При проектировании объекта на плоскость нужно провести через каждую точку объекта прямую из заданного проектирующего пучка и найти пересечение этой прямой с плоскостью.

При параллельном проектировании пучок состоит из параллельных прямых, при центральном – проходит через некоторую точку.

Параллельные проекции можно разделить на два типа, когда прямые пучка перпендикулярны плоскости проектирования – проекции называют аксонометрическими, а когда нет, косоугольными (такие проекции мы рассматривать не будем).

Таким образом, чтобы получить аксонометрическую параллельную проекцию объекта на экране нужно совместить направление пучка с одной из осей (обычно это Z). Оси X и Y совпадут с осями X,Y на экране, а ось Z – будет направлена вглубь экрана.

Чтобы получить перспективную проекцию точки необходимо поместить точку схода пучка в начало координат, направление на экран (перпендикуляр из точки схода к плоскости проектирования) совместить с осью Z, тогда Xp=X*d/Z, Yp=Y*d/Z, где d - расстояние от начала координат до плоскости проектирования.

Это преобразование можно записать в виде матрицы. ,

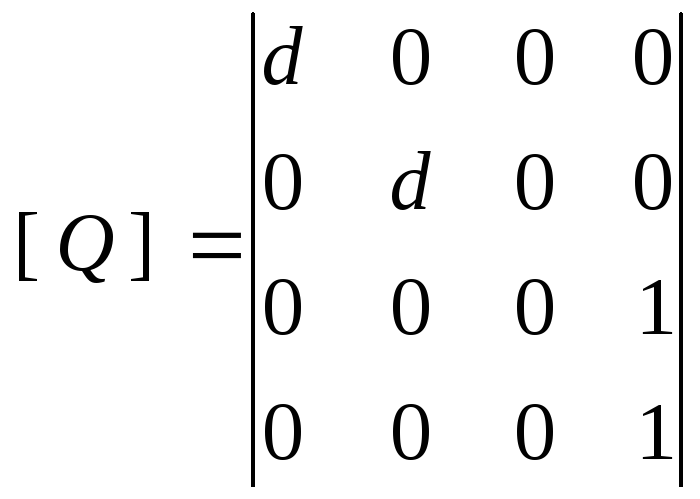тогда

Е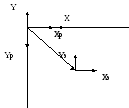динственное, в таком преобразовании теряется глубина (z), но можно ее вычислить из последней координаты вектора.

Кроме этих преобразований проектирования необходимо сделать еще несколько, чтобы изображение правильно смотрелось на экране. Во-первых, его нужно растянуть до размеров окна, во-вторых, его нужно зеркально отобразить вокруг оси Х (т.к. ось Y обычно направлена вниз), в-третьих, его нужно перенести в центр окна.

Общая матрица преобразования выглядит следующим образом.

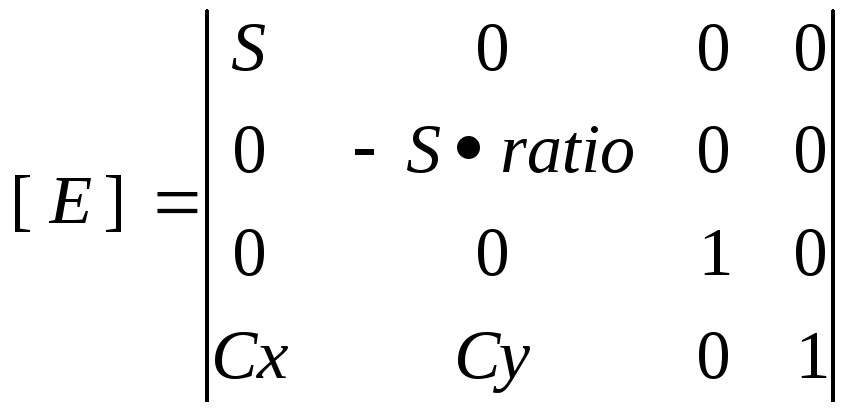
Cx,Cy – координаты центра экрана.

ratio – отношение размера по Y к размеру по X, для разных разрешений экрана разный. Разрешение – количество точек на единицу поверхности, в данном случае единица – весь экран монитора. Экран монитора имеет соотношение горизонтального размера к вертикальному 4/3, поэтому для разрешений с количеством точек по горизонтали и вертикали кратным этому числу ratio=1 (например 640/480). Иначе ratio=(4*sizey)/(3*sizex) (320x200 =0.83).

S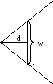 – масштабный коэффициент, для параллельной проекции выбирается вручную, для перспективной проекции S равняется единице, но рассчитывается d (расстояние до плоскости проектирования) исходя из поля зрения FOV (field of view). FOV – максимальный угол, который образуют прямые в пучке, угол зрения.

FOV обычно варьируется от 50 до 100, FOV человеческого глаза - 90.

Мировая, модельная и экранная системы координат

Мировая – основная система координат, в которой заданы все объекты сцены.

Модельная – система координат, в которой задана внутренняя структура объектов.

Экранная –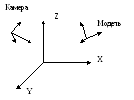 система координат наблюдателя, еще ее называют системой координат камеры.

Модель обычно располагают в модельной системе таким образом, что центр системы совпадает либо с геометрическим, либо с центром масс модели, ось X совпадает с направлением вперед, ось Y – вправо, ось Z – вверх.

Модель задается в мировой системе координат координатами центра модели M (вектор) и ориентацией (либо тремя ортами, либо тремя углами крен (X), тангаж (Y), курс (Z), матрица при этом формируется как последовательность поворотов [Rx][Ry][Rz]). Для преобразования из модельных координат нужно сначала повернуть в соответствии с матрицей ориентации [Rm], а затем перенести на [T(M)].

Курс Крен Тангаж

Положение и ориентацию камеры можно задать точно так же, как и положение модели. Но часто, достаточно только направления зрения камеры. Обычно (в реальной жизни) камера не имеет крена, т.е. ось X (вправо) всегда горизонтальна, а плоскость YZ следовательно всегда вертикальна.

Таким образом, если предположить, что ось Z камеры (направление зрения) не вертикальна, то можно найти ось X=Norm(ZUp), где Up(0,0,1) вертикальный вектор (X получится перпендикулярен вертикальному вектору Up, а значит горизонтален). Наконец ось Y=XZ (вверх). Следите за тем, чтобы система оставалась левой.

Чтобы преобразовать точки из мировой системы в экранные необходимо сначала применить перенос [T(-C)], а затем повернуть на транспонированную матрицу ориентации камеры [Rс]^T.

Таким образом, для того, чтобы перевести точку из модельных координат в экранные необходимо произвести следующее преобразование [Rm][T(M)][T(-C)] [Rс]^T. После таких преобразований ось Z будет направлена вдоль направления зрения и можно делать проектирование.