Способы задания графов. Матричное задание графов.

Существует несколько способов задания графов:

1. Перечисление (список) ребер графа и вершин графа.

2. В виде геометрического объекта (реализация).

3. Матричный способ

а) матрица смежности А;

б) матрица инцидентности В.

Пусть Д=(V, X) – орграф, где V={v₁, …, v_n}, X={x₁, …, x_m}

Определение: Матрицей смежности орграфа Д называется квадратная матрица A(Д)= [a_ij] порядка n, у которой

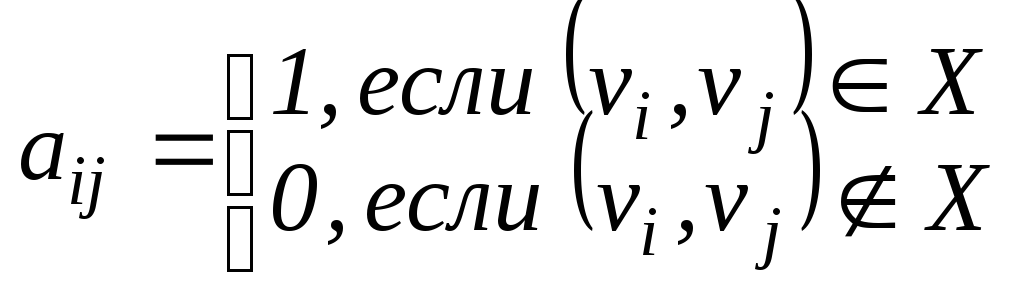
Определение: Матрицей инцидентности (или матрицей инциденций) орграфа Д называется матрица B(Д)=[в_ij] размерности n x m, у которой

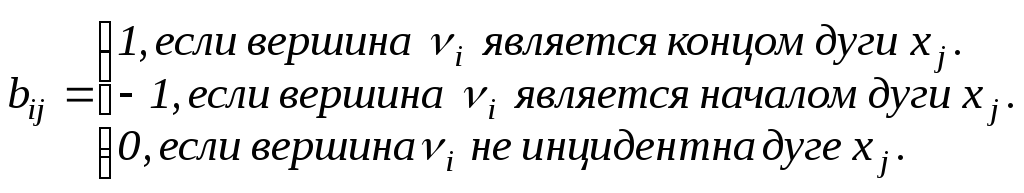
Пусть G=(V, X) – неориентированный граф, где V={v₁, …, v_n}, X={x₁, …, x_m}

Определение: Матрицей смежности графа G называется квадратная матрица A(G)=[a_ij] порядка n, у которой

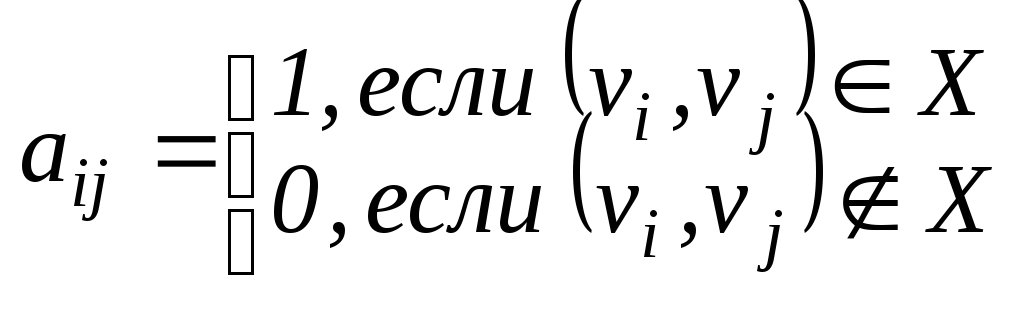
Определение: Матрицей инцидентности графа G называется матрица B(G)=[в_ij] размерности n x m, у которой

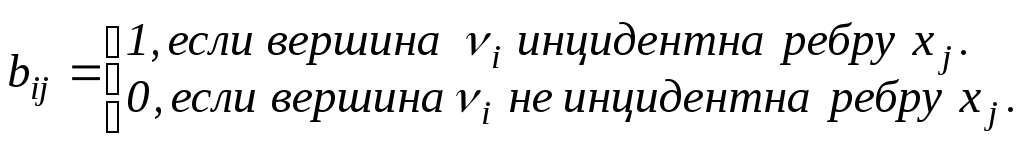
Замечание: Матрицу смежности можно определить и для псевдографов. Тогда в случае ориентированного (неориентированного) псевдографа a_ij=k , где k – кратность дуги (ребра) (v_i, v_j) в этом псевдографе. Определение матрицы инцидентности без изменений переносится и на произвольные мультиграфы (ориентированные и неориентированные) и на неориентированные псевдографы; только в случае петли (v_i, v_i) ставим в матрице инцидентности α.

Матрица A(G) является симметричной для любого неориентированного графа G.

Матрица A(Д), где Д – орграф, в общем случае симметричной не является.

По матрице смежности графа (орграфа) всегда можно определить ребра графа (дуги орграфа) как пары инцидентных им вершин, а для псевдографов, кроме того, и кратность ребер (дуг).

Однако, если рёбра (дуги) были пронумерованы, то восстановить их номера по матрице смежности невозможно.

В этом случае более информативной оказывается матрица инцидентности.

Свойства матриц смежности и инцидентности

1. Пусть G=(V, X) – мультиграф (V={v₁, …, v_n}). Тогда сумма элементов матрицы A(G) по i-ой строке (или по i-му столбцу) равна .

2. Пусть Д=(V, X) – ориентированный псевдограф (V={v₁, …, v_n}). Сумма элементов матрицы A(Д) по i-ой строке равна , сумма элементов по i-му столбцу равна .

3. Пусть Д=(V, X) – ориентированный мультиграф. Тогда

а) сумма строк матрицы B(Д) является нулевой строкой;

б) любая строка матрицы B(Д) является линейной комбинацией остальных строк;

в) rang B(Д) n(Д)-1 (n(Д) – кол-во вершин);

г) для любого контура в Д сумма столбцов матрицы В(Д), соответствующих дугам, входящим в этот контур, равна нулевому столбцу.

4. Пусть G – мультиграф с непустым множеством ребер. Тогда при покоординатном сложении по модулю 2:

а) сумма строк матрицы В(G) является нулевой строкой;

б) любая строка матрицы B(G) является суммой остальных строк;

в) для любого цикла в G сумма столбцов матрицы B(G), соответствующих рёбрам, входящим в этот цикл, равна нулевому столбцу.

Обозначим через A^k=[a_ij^(k)] – k-тую степень матрицы смежности A.

Утверждение 1. Элемент a_ij^(k) матрицы A^(k) ориентированного псевдографа Д=(V, X) (псевдографа G=(V, X)), где V={v₁, …, v_n} равен числу всех путей (маршрутов длины k) из v_i в v_j.

Утверждение 2. Для того, чтобы n-вершинный орграф Д с матрицей смежности А=А(Д) имел хотя бы один контур, необходимо и достаточно, чтобы матрица K=A²+A³+…+Aⁿ имела ненулевые диагональные элементы.

Утверждение 3. Для того, чтобы n-вершинный ориентированный псевдограф Д с матрицей смежности А=А(Д) имел хотя бы один контур, необходимо и достаточно, чтобы матрица K=A+A²+…+Aⁿ имела ненулевые диагональные элементы.