§ 10. Раскраска графов. Планарные графы Раскраска вершин графа

Пусть дан неориентированный граф G=(V,X).

Определение: Раскраской вершин графа называется сопоставление (приписывание) цветов вершинам графа.

Определение: Раскраска называется правильной, если смежные вершины окрашены в разные цвета.

Определение: Наименьшее число цветов, необходимых для правильной раскраски? называется хроматическим числом и обозначается χ(G).

Определение: Неориентированный граф G называется бихроматическим, если χ (G)=2

Примеры:

1) G: χ (G)=2

2) χ (K_m,n)=2

Теорема: Для того, чтобы граф, содержащий хотя бы одно ребро, был бихроматическим, необходимо и достаточно, чтобы он не содержал элементарных циклов нечетной длины.

В полном графе K_n любые две различные вершины связаны ребром? Gj’njve χ (K_n) = n

Определение: Множество вершин, окрашенных в один цвет, называется одноцветным классом.

Одноцветные классы образуют независимые множества вершин.

Определение: Множество вершин называется независимым, если никакие две из них не являются смежными.

Определение: Наибольшее число вершин в независимом множестве называется вершинным числом независимости и обозначается ₀(G).

Примеры:

1. G: М₁={1, 3}

M₂={2}

M₃={1, 4}

M₄={3, 5}

М₁, M₂, M₃, M₄ – независимые множества, β₀(G)=2

2.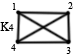

M₁ ={1}

M₂ ={2}

M₃ ={3}

M₄ ={4}

₀(K₄)=1

3.

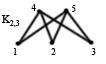
M₁ ={1, 2, 3}

M₂={4, 5}

₀(K_2,3) = 3

Теорема: ₀ (K_n) = 1.

Теорема: ₀ (K_m,n) = max (m;n).

Теорема:

.

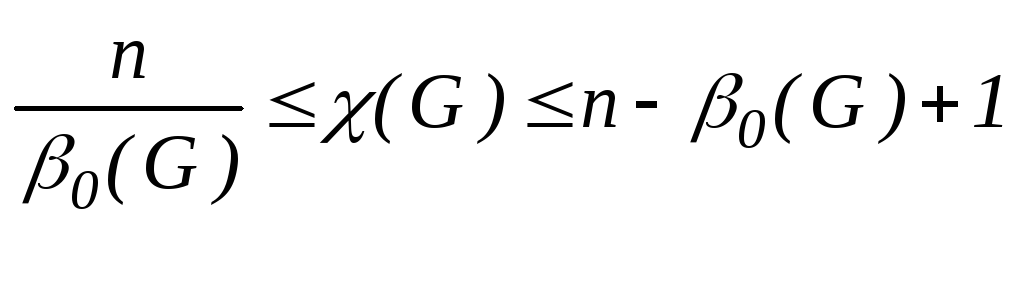Пример:

G:

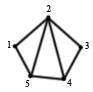
₀=2, тогда

5/2≤ χ ≤5-2+1 и χ (G)=3

Таким образом, для правильной раскраски G необходимо 3 краски.

Точный алгоритм раскрашивания:

1. Выбрать в графе G некоторое максимальное независимое множество вершин М.

2. Покрасить вершины множества М в очередной цвет.

3. Пусть G=G\M и перейти к шагу 1.

Алгоритм выполняется до тех пор, пока не будут покрашены все вершины.

Существуют и приближенные алгоритмы раскрашивания:

1. алгоритм последовательного раскрашивания вершин;

2. улучшенный алгоритм последовательного раскрашивания (начинать раскрашивать следует с вершины наибольшей степени, т.к. если их раскрашивать в конце процесса, то более вероятно, что для них не найдется свободного цвета и придется задействовать еще один цвет).

Многие практические задачи сводятся к построению раскраски вершин графа.

Например:

1. Раскраска географической карты мира.

Пусть G=(V; X), где V – множество вершин – множество стран, Х – множество ребер – ребра соединяют страны, имеющие общую границу.

Числу χ (G) соответствует наименьшее число красок, необходимых для раскраски карты так, чтобы никакие две соседние страны не были окрашены в один цвет.

2. Задача составления расписания.

Предположим, что нужно прочесть несколько лекций за кратчайшее время. Чтение каждой лекции в отдельности занимает один час, но некоторые лекции не могут читаться одновременно (например, их читает один и тот же лектор). Построим граф G=(V;X), где V-множество лекций, X- множество рёбер (рёбра соединяют те вершины, т.е. лекции, которые нельзя читать одновременно).

Следовательно, любая раскраска этого графа определяет допустимое расписание: лекции, соответствующие вершинам одного цвета, могут читаться одновременно. Оптимальные расписания соответствуют раскраскам с минимальным числом цветов, а число часов, необходимое для прочтения всех лекций, равно χ (G).

Существуют и практические задачи, связанные с раскраской рёбер в графе.

Раскраска рёбер может быть определена с помощью раскраски вершин соответствующего рёберного графа. Раскраской рёбер графа G называется раскраска вершин графа G_p.

Пример: Проводится монтаж аппаратуры. Чтобы не перепутать проводники, необходимо их окрасить таким образом, чтобы два проводника, идущие к одной плате, имели разные цвета. В этом случае вершинами являются платы, а рёбрами – проводники.

Теорема: Если граф G – лес, то χ (G) ≤ 2.

Теорема: Для любого неорграфа G без петель выполняется неравенство χ(G) ≤ s+1 (s – максимальная степень вершин графа G).

Определение правильности раскраски распространяется и на неполные раскраски, т.е. такие, при которых не обязательно все вершины (рёбра) окрашены.

Существуют тотальные раскраски – раскраски, при которых окрашиваются как вершины, так и рёбра, а правильность означает, что никакие два смежных или инцидентных элемента не должны иметь одинаковый цвет.

Определение: Неорграф G называется планарным, если его можно изобразить на плоскости так, что никакие два ребра не будут иметь общих точек, кроме вершин графа.

Такое изображение графа на плоскости называется плоским. Таким образом, если граф имеет плоское изображение, то он является планарным.

Пример:

Его плоские

и

К₄

зображения: или

Определение: Область, ограниченная рёбрами в плоском графе и не содержащая внутри себя вершин и рёбер, называется гранью планарного графа.

Число граней планарного графа будем обозначать: Г.

Различают внутренние и внешние грани.

Пример:

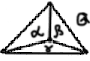
, , γ – внутренние грани

 – внешняя грань

Не всякий граф является планарным.

Теорема 1: В связном планарном графе G=(V,X) V={v₁,…, v _n}, X={x₁,…,x_m} справедливо равенство:

Замечание: Эйлер вывел формулу, исследуя многогранники. Развёртка многогранника – это и есть плоское представление многогранника, т.е. планарный граф.

Следствия:

1. если G – связный неориентированный планарный граф (n>3), то m≤ 3n-6;

2. графы К₅ и К_3,3 непланарны;

3. в любом планарном графе существует вершина, степень которой не больше 5.

Теорема 2 (Понтрягина-Куратовского): Граф G планарен тогда и только тогда, когда он не содержит в качестве подграфов ни К₅, ни К_3,3.

Известна оценка хроматического числа планарных графов.

Теорема 3: Всякий планарный граф можно раскрасить пятью красками.

Теорема 4 (гипотеза 4-х красок): Если граф G-планарный, то

χ (G) ≤4.

(Впервые проблема о 4-х красках была сформулирована британским математиком А. Кэли в 1879 г.).

При исследовании принципиальной электрической схемы радиоэлектронного устройства с точки зрения возможности её реализации с помощью печатного монтажа или монтажа на слоях микросхемы конструктору важно знать ответ на следующие вопросы:

1. является ли граф, соответствующий рассматриваемой схеме, планарным?

2. если граф планарен, то как получить его изображение без пересечения рёбер?

На первый вопрос ответ дает теорема Понтрягина-Куратовского. Методы получения плоских изображений планарных графов можно найти в книге Б. Н. Деньдобренко, А. С. Малика «Автоматизация конструирования», М., 1980.

Если граф G непланарен, то для его геометрической реализации удаляют отдельные ребра (переносят на другую плоскость). Минимальное число рёбер, которые необходимо удалить из графа для получения его плоского изображения, называется числом планарности графа G. При вынесении этих рёбер на вторую плоскость получают часть графа, которая также может оказаться неплоской. Тогда вновь решают задачу вынесения отдельных рёбер на следующую плоскость и т.д. Минимальное число плоскостей m, при котором граф G разбивается на плоские части G₁, G₂, … ,G_m (разбиение ведётся по множеству рёбер), называется толщиной графа G. Таким образом, толщина планарного графа равна 1, а графы К₅ и К_3,3 имеют толщину равную 2.