Упражнения

8.1. Выяснить, имеются ли в графах эйлеровы цепи, циклы. Если да, то выделить их, используя алгоритмы.

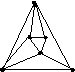а) б) в)

8.2. Нарисовать восьмивершинный граф, который:

а) имеет эйлеров цикл;

б) имеет эйлерову цепь;

в) не имеет ни эйлерова цикла, ни эйлеровой цепи;

г) имеет гамильтонов цикл;

д) имеет гамильтонову цепь;

е) не имеет ни гамильтона цикла, ни гамильтоновой цепи;

ж) имеет гамильтонов цикл, но не имеет эйлерова цикла;

з) имеет эйлеров цикл, но не имеет гамильтонова цикла.

8.3. На рисунке изображена схема, на которой точкой отмечен магазин, а остальными вершинами – места жительства заказчиков. Как водителю машины «Доставка на дом» объехать всех заказчиков, не подъезжая ни к одному дому более одного раза?

М

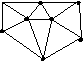
8.4. На рисунке изображена схема зоопарка (вершины графа – вход, выход, перекрестки, повороты, тупики; ребра – дорожки, вдоль которых расположены клетки). Найти маршрут, по которому экскурсовод мог бы провести посетителей, показав им всех зверей и не проходя более одного раза ни одного участка пути.

ВХОД

ВЫХОД

8.5. Сможет ли экскурсовод провести посетителей по выставке так, чтобы они побывали в каждом зале ровно один раз? Соответствующий граф приведен на рисунке. Вершины графа – это вход, выход, двери, соединяющие залы, перекрестки, а ребра – залы и коридоры.

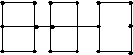
8.6. На рисунке изображен план подземелья, в одной из комнат которого скрыты богатства рыцаря. После смерти рыцаря его наследники нашли завещание, в котором было сказано, что для отыскания сокровищ достаточно войти в одну из крайних комнат подземелья, пройти через все двери, причем в точности по одному разу через каждую; сокровища скрыты за той дверью, которая будут пройдена последней. В какой комнате были скрыты сокровища?

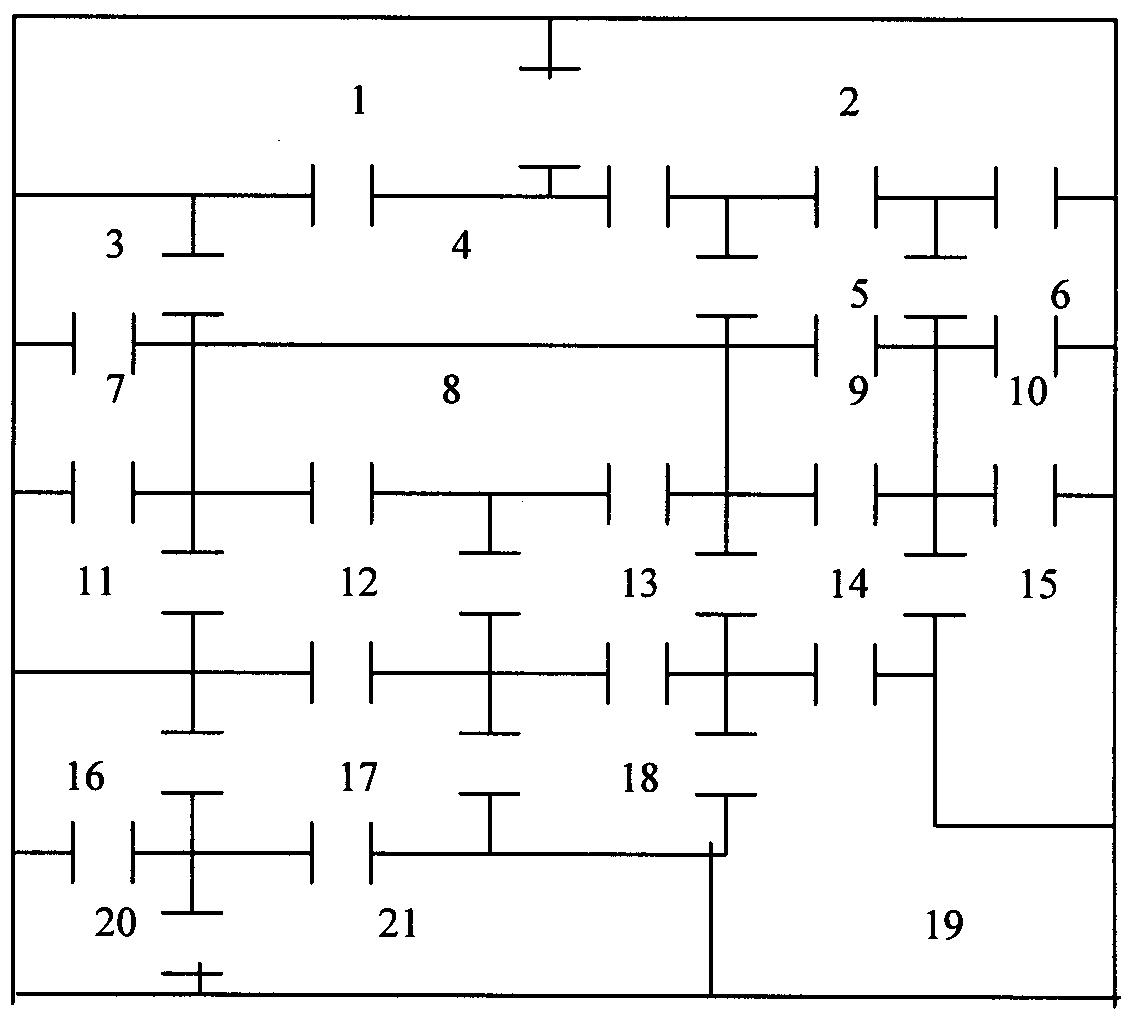
§ 9. Деревья. Остов графа. Цикловой базис графа

Определение: Связный граф без циклов называется деревом.

Примеры:

Определение: Граф G, все компоненты связности которого являются деревьями, называют лесом.

Свойства деревьев:

Если граф G – дерево, то:

1. G – связный;

2. G не имеет простых циклов;

3. Если G имеет n вершин, то ребер (n-1);

4. Если у дерева G есть, по крайней мере, одно ребро, то у него обязательно найдётся висячая вершина;

5. Любые две различные вершины графа G можно соединить единственной простой цепью;

6. При добавлении к дереву любого нового графа получаем ровно один и притом простой цикл, который проходит через добавленное ребро.

При решении прикладных задач часто возникает необходимость обхода вершин графа, связанная с поиском вершин, удовлетворяющих определенным свойствам. Тогда если граф есть дерево, то его удобно изображать следующим образом. Выберем в дереве произвольную вершину α₀ и назовем её корнем дерева (или вершина нулевого яруса). Смежные с α₀ вершины назовем вершинами 1-го яруса и т.д.

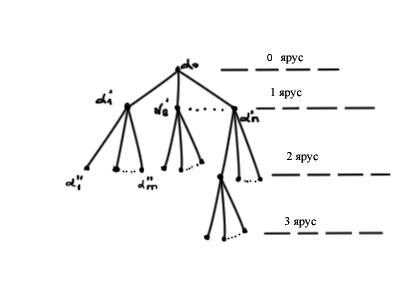
Номер яруса совпадает с расстоянием между его вершинами и корнем дерева.

Выделение корня в дереве определяет на множестве его вершин частичный порядок: .

Корень ₀ является единственным минимальным элементом в этом частичном упорядоченном множестве вершин, а все концевые вершины – максимальные элементы.

Определение: Остов графа G (или остовное дерево, или каркас графа G) – любой подграф графа G, содержащий все вершины графа G и являющийся деревом.

Если в связном графе G будем последовательно удалять циклические ребра до тех пор, пока это возможно, т.е. пока не останется ни одного циклического ребра, то мы придем к связному подграфу графа G с тем же множеством вершин, но без элементарных циклов, т.е. к дереву (остову).

Остов выбирается, вообще говоря, неоднозначно, в него входят все ациклические ребра.

Пусть G – граф, Д – его остов. Тогда все ребра подграфа G\Д называются хордами. Каждая хорда связывает две вершины остова.

На практике удобнее строить остов графа G путем последовательного удаления из G циклических ребер (хорд).

Пусть дан граф G=(V,X) v={v₁,…, v _n}, X={x₁,…,x_m}.

В остове графа G ребер будет (n-1) .

Тогда из графа G при построении остова удаляется m-(n-1)=m-n+1 ребер, т.е. m-n+1 – количество хорд (количество удаленных циклических ребер).

Определение: Число m-n+1 называется цикломатическим числом связного графа G и обозначается v(G) (или циклическим рангом).

Определение: Независимая система циклов {₁,…,_n} называется цикловым базисом мультиграфа G, любой цикл из графа G является линейной комбинацией циклов этой системы.

Утверждение: Если мультиграф G не является ациклическим, то в нём существует цикловой базис, элементами которого являются простые циклы.

Теорема: Количество элементов в цикловом базисе мультиграфа G=(V,X) совпадает с его цикломатическим числом. То есть цикломатическое число показывает, чему равна размерность пространства базисов циклов графа.

Для несвязного графа с к компонентами связности базис циклов графа получается объединением базисов его связных компонент.

Утверждение 1: Неорграф G является лесом тогда и только тогда, когда υ(G)=0.

Утверждение 2: Неорграф G имеет единственный цикл тогда и только тогда, когда υ(G)=1.