§ 7. Нагруженные графы. Расстояния в нагруженном графе
Определение: Граф G = (V, X) (орграф Д = (V, X)) называется нагруженным, если на множестве ребер (дуг) определена некоторая функция l: X → R , которую часто называют весовой функцией.
Таким образом, в
нагруженном графе (нагруженном орграфе)
каждому ребру (дуге) x
X поставлено в соответствие некоторое
действительное число l(x).
Значение l(x) называется длиной ребра (дуги) x или весом ребра (дуги) x.
Пример:
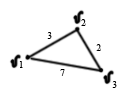
l( v1, v2)=3
l( v2, v3)=2
l( v1, v3)=7
Информацию о длинах дуг (ребер) нагруженного орграфа (графа) можно представить в виде матрицы длин дуг (ребер).
Определение: Матрицей длин дуг (ребер) орграфа Д (графа G) называется квадратная матрица порядка n С= [сij], у которой каждый элемент сij определяется следующим образом:
Определение: Пусть дан нагруженный граф G = (V, X) (орграф Д = (V, X)).
Рассмотрим некоторый маршрут (путь) из вершины vi в вершину vj. Обозначим его П, а сумму длин входящих в него ребер (дуг) обозначим l(П).
l(П) называется длиной маршрута (пути) П в нагруженном графе (орграфе) или весом маршрута (пути).
Пример: Пусть П – маршрут из v1 в v3.
П1 = v1 v2 v3 П2 = v1 v3
l(П1) = 3 + 2 = 5 l(П2) = 7
Определение: Расстоянием в нагруженном графе (орграфе) (или взвешенным расстоянием) между вершинами vi и vj называется длина минимального маршрута (пути) из vi в vj.
Матрица взвешенных расстояний, взвешенные эксцентриситеты вершин, диаметр, радиус, центр нагруженного графа определяются аналогично определению данных понятий для ненагруженного графа.
Нахождение минимального пути в нагруженном орграфе
Существует несколько алгоритмов нахождения кратчайшего маршрута в нагруженном графе:
Алгоритм Форда – Беллмана.
Алгоритм Дейкстры.
Пусть Д=(V,X) – нагруженный орграф. V={v1,…,vn}.
C(Д)nxn=[cij] – матрица длин дуг нагруженного орграфа.
Величина i(k), где i=1,…,n; k=1,2,… , равна длине минимального пути среди путей из v1 в vi, содержащих не более k дуг. Если таких путей нет, то i(k)=. 1(0) =0, i(0)=, i=2,…,n.
Утверждение:
При
i=2,…,n, k≥0:
При
i=1, k≥0:
Число дуг в простой цепи не превосходит n-1. Следовательно, i(k)= i(n-1) i=2,..,n,k≥n-1.
Если i(n-1)= (i {2,..,n}), то vi не достижима из v1, а если i(n-1), то vi достижима из v1 и при этом i(n-1) –длина минимального пути из v1 в vi.
Таким образом, по i(n-1) можно судить о достижимости вершин vi (i=2,…,n) из v1, а также определить длины минимальных путей из v1 в достижимые вершины.
Алгоритм Форда-Беллмана нахождения минимального пути в нагруженном орграфе из v1 в vi1 (i1≠1)
Шаг 1: Пусть таблица
величин i(k)(i=1,2,…,n;k=0,1,…,n-1)
составлена. Если
,
то вершина
не достижима из
.
В этом случае работа алгоритма
заканчивается.
Шаг 2: Пусть
.
Тогда число
выражает
длину любого минимального пути из
в
в нагруженном орграфе Д.
Определим
минимальное число k1≥1,
при котором выполняется равенство
.
По определению чисел i(k)
получаем, что k1 –
минимальное число дуг в пути среди всех
минимальных путей из
в
в
нагруженном орграфе Д.
Шаг 3: Последовательно
определяем номера
такие, что:
(*)
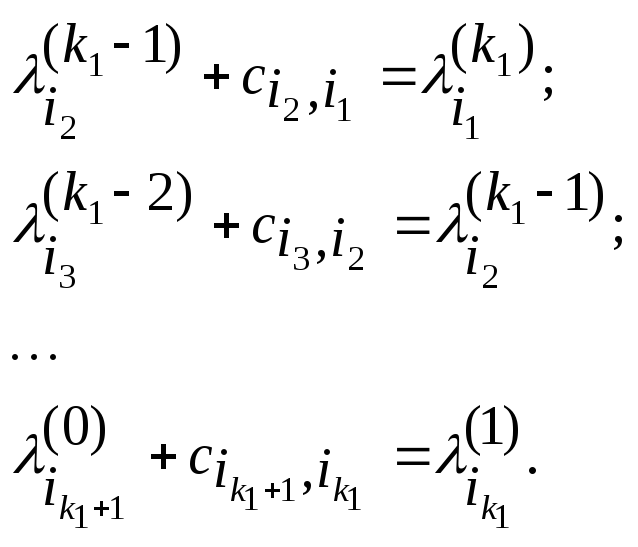Из ()
с учетом того, что
,имеем
(1)
Складывая
равенства () и
учитывая (1) получаем:
,
т.е.
-
искомый минимальный путь из
в
в
нагруженном орграфе Д.
В этом пути ровно
k1 дуг. Следовательно,
мы определили путь с минимальным числом
дуг среди всех минимальных путей из
в
в нагруженном орграфе Д.