
- •Содержание
- •Введение
- •Часть 1. Элементы теории множеств и отношений § 1. Понятие множества. Операции над множествами
- •Примеры
- •Операции над множествами
- •Основные тождества алгебры множеств
- •Упражнения
- •§ 2. Декартово произведение двух или нескольких множеств. Понятие отношения. Бинарные отношения
- •Упражнения
- •§ 3. Специальные бинарные отношения. Отношения эквивалентности
- •Упражнения
- •§ 4. Отношения порядка
- •Упражнения
- •§ 5. Функциональные отношения (отображения). Виды отображений
- •Виды отображений:
- •Упражнения
- •Часть 2. Теория графов
- •§ 1. Основные понятия теории графов
- •Способы задания графов. Матричное задание графов.
- •Свойства матриц смежности и инцидентности
- •Упражнения
- •§ Б 2. Булевы матрицы
- •Дизъюнкция (конъюкция)
- •§ 3. Связность графа. Компоненты связности. Матрица связности
- •Выделение компонент связности
- •Алгоритм выделения компонент сильной связности
- •Упражнения
- •§ 4. Полные графы. Двудольные графы. Однородные и реберные графы
- •Упражнения
- •§ 5. Поиск путей (маршрутов) с минимальным числом дуг (ребер)
- •Упражнения
- •§ 6. Расстояние в графах
- •Упражнения
- •§ 7. Нагруженные графы. Расстояния в нагруженном графе
- •Нахождение минимального пути в нагруженном орграфе
- •Алгоритм Форда-Беллмана нахождения минимального пути в нагруженном орграфе из v1 в vi1 (i1≠1)
- •Упражнения
- •§ 8. Эйлеровы цепи и циклы в графах. Эйлеровы графы. Гамильтоновы цепи и циклы в графах. Гамильтоновы графы
- •Упражнения
- •§ 9. Деревья. Остов графа. Цикловой базис графа
- •Алгоритм нахождения кратчайшего остова в нагруженном графе
- •Упражнения
- •§ 10. Раскраска графов. Планарные графы Раскраска вершин графа
- •Одноцветные классы образуют независимые множества вершин.
- •Существуют и приближенные алгоритмы раскрашивания:
- •Упражнения
- •Варианты контрольных работ Часть 1. Элементы теории множеств и отношений Вариант № 1.
- •Вариант № 2.
- •Вариант № 3.
- •Вариант № 4.
- •Вариант № 5.
- •Вариант № 6.
- •Часть 2. Теория графов Вариант № 1.
- •Вариант № 2.
- •Вариант № 3.
- •Вариант № 4.
- •Вариант № 5.
- •Вариант № 6.
- •Ответы Часть 1
- •Часть 2
- •Тест по теории множеств и отношений
- •Тест по теории графов
- •Библиографический список
- •Любовь Васильевна Архипова Елена Сергеевна Дернович
- •Дискретная математика
Упражнения
5.1. Определить минимальные пути из вершины v1 в вершину v7, из вершины v2 в вершину v5 в орграфе, заданном матрицей смежности. Построить граф.
а) б)
А
=
 А =
А =

Определить количество минимальных путей.
5.2. Найти все кратчайшие пути из вершины v1 во все остальные в орграфе:
А =

§ 6. Расстояние в графах
Пусть G = (V, X) – связный неориентированный граф.
v 1, v 2 – две его несовпадающие вершины.
Определение: Расстоянием между вершинами v i и v j называется длина кратчайшего (v i , v j) – маршрута. Обозначается ρ (v i , v j).
Введенное таким образом расстояние удовлетворяет следующим аксиомам метрики:
-
ρ (v i , v j) ≥ 0;
-
ρ (v i , v j) = 0 <=> v i = v j (если i = j);
-
ρ (v i , v j) = ρ (v i , v j) – симметричность;
-
ρ (v i , v j) ≤ ρ (v i ,w) + ρ (w , v j) – неравенство треугольника;
-
ρ (v i , v j) < ∞
Определение: Пусть G = (V, X). Если V = { v 1, v 2, …, v n}, то матрицей расстояний называется матрица P = [ p ij] порядка n, у которой:
p ij = ρ(v i,v j) (i = 1,…, n; j = 1,…, n)
Замечание: PT = P, т. е. матрица P симметрична.
Определение: Для фиксированной вершины v величина
е(v)
= max {ρ(v,w) | w![]() V}
называется эксцентриситетом
вершины v. Таким образом,
эксцентриситет вершины равен расстоянию
от данной вершины до наиболее удаленной
от нее.
V}
называется эксцентриситетом
вершины v. Таким образом,
эксцентриситет вершины равен расстоянию
от данной вершины до наиболее удаленной
от нее.
Если P – матрица расстояний, то эксцентриситет е(v i) равен наибольшему из чисел, стоящих в i-й строке.
Определение: Диаметром графа G называется эксцентриситет, максимальный среди всех эксцентриситетов вершин.
Обозначается
d(G). d(G) = max
{е(v i)
/ v i
![]() V
}.
V
}.
Определение: Вершина v называется периферийной, если е(v) = d(G).
Определение:
Минимальный из эксцентриситетов
графа G называется его радиусом.
Обозначается r(G),
т. е. r(G) =
min {е(v
i) | v
i
![]() V
}.
V
}.
Определение: Вершина v называется центральной, если е(v) = r(G).
Определение: Множество всех центральных вершин графа называeтся его центром.
Пример:
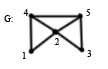
Составим
матрицу расстояний P =
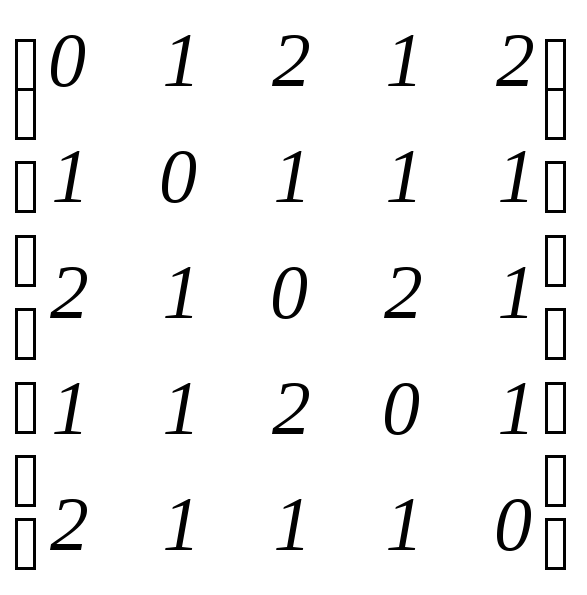
e(1) = 2, e(2) = 1, e(3) = 2. e(4) = 2, e(5) = 2, тогда
d(G) = 2. Периферийные вершины: 1, 3, 4, 5.
r(G) = 1, центр {2}. (центр может состоять из нескольких вершин).
Теорема: В полном графе Kn d(Kn) = r(Kn) = 1 (т. к. все различные вершины графа Kn смежны).
Задача нахождения центральных вершин возникает в практической деятельности людей.
Например, граф представляет собой сеть дорог, т. е. вершины соответствуют населенным пунктам, а ребра – дорогам между ними. Требуется оптимально разместить больницы, пункты обслуживания и т. п. В подобных ситуациях оптимизация заключается в минимизации расстояния от места обслуживания до наиболее удаленного населенного пункта. Следовательно, местами размещения должны быть центральные вершины графа. Реальные задачи отличаются от этой идеальной тем, что приходится учитывать и другие обстоятельства – расстояния между населенными пунктами, стоимость, время проезда и т. д. Для учета этих параметров используются взвешенные графы (нагруженные).
Упражнения
6.1. Составить матрицу расстояний, найти диаметр, радиус и центр графа:
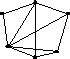
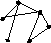
а)
б) в) А=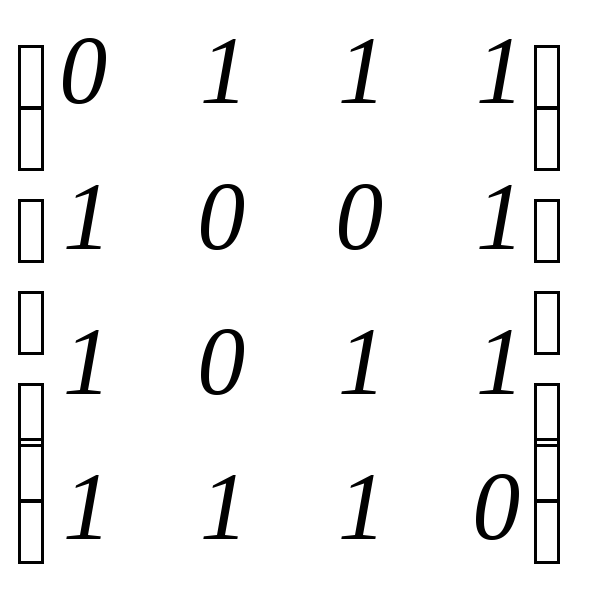
6.2. Найти диаметр, радиус, центр графа:
а) К5
б) К2,3
в) Е3
6.3. Найти диаметр, радиус, центр графа, заданного матрицей смежности:
а) б)
б)![]()
6.4. Построить шестивершинный граф с d=4 и r=2.
