Алгоритм выделения компонент сильной связности

Пусть Д=(V,X) – орграф, матрица связности S(Д), p – количество компонент сильной связности. Д₁,…,Д_р – компоненты сильной связности, А(Д₁),…,А(Д_р) – матрицы смежности, S₁,... S_p – матрицы связности компонент сильной связности.

1. Полагаем, что р=1, S₁=S(Д).

2. Включаем в множество вершин V_p очередной компоненты сильной связности Д_р орграфа Д вершины, соответствующие единицам первой строки матрицы S_p. В качестве А(Д_р) берем подматрицу матрицы А(Д), находящуюся на пересечении строк и столбцов, соответствующих вершинам из V_p.

3. Вычеркиваем из S_p строки и столбцы соответствующие вершинам из V_p. Если в результате такого вычеркивания не остаётся ни одной строки (и соответственно ни одного столбца), то р – количество компонент сильной связности и А(Д₁),…,А(Д_р) – матрицы смежности компонент сильной связности Д₁,…,Д_р орграфа Д. В противном случае обозначаем оставшуюся после вычеркивания из S_p соответствующих строк и столбцов матрицу через S_p+1, присваиваем р:=р+1 и переходим к шагу 2.

Аналогичный алгоритм можно записать и для определения числа компонент связности графа G.

Упражнения

3.1. К какому типу относятся графы (связный, сильно связный, односторонне связный, слабо связный)? Составить матрицы связности (сильной связности) графа (орграфа). Указать количество компонент связности (сильной связности).

а)

б)

в)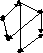

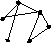
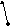
3.2. Определить матрицы связности для графов с матрицами смежности:

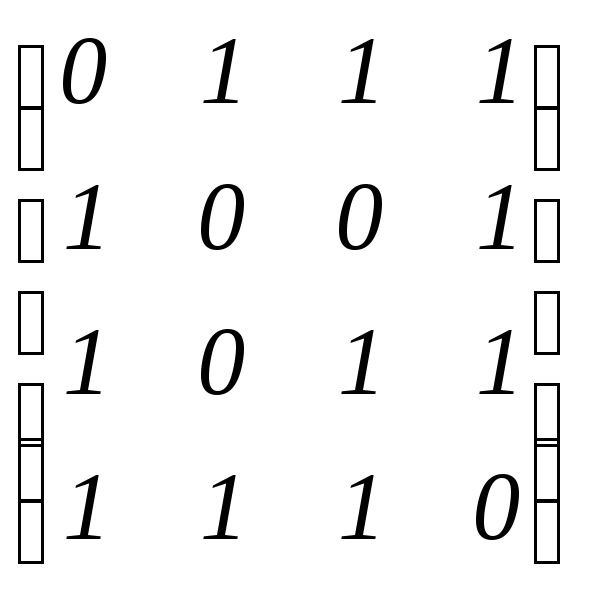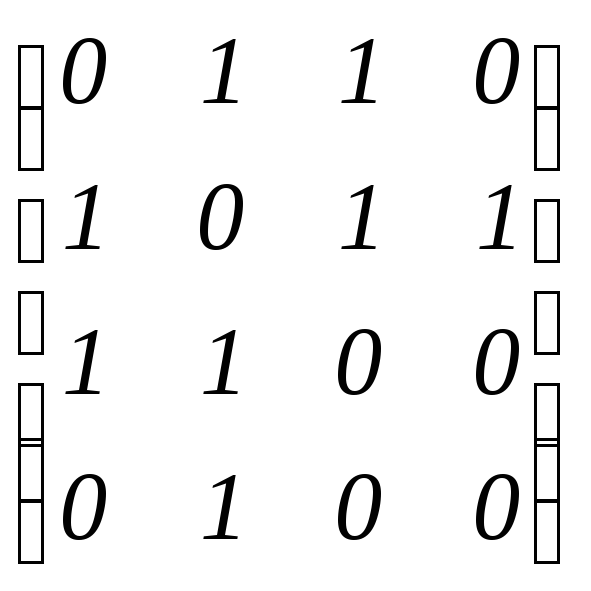а) б) в)

3.3. Пусть орграф D задан матрицей смежности. Определить матрицу сильной связности S(D). Используя алгоритм, найти количество компонент сильной связности орграфа D и определить матрицы смежности этих компонент. Построить изображения орграфа D и его компонент сильной связности.

а

) б)

§ 4. Полные графы. Двудольные графы. Однородные и реберные графы

Определение: Граф называется полным, если любые две различные вершины его соединены одним и только одним ребром (или если любые его две вершины смежны).

Полный неориентированный граф с n вершинами обозначается K_n.

К₃:

К₄:

К₅: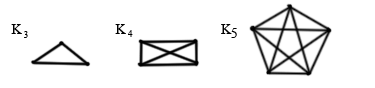

Граф G, не являющийся полным, можно преобразовать в полный с теми же вершинами, добавив недостающие ребра. Вершины графа G и ребра, которые добавлены, также образуют граф. Он называется дополнением графа G до полного графа.

Определение: Дополнением графа G называется граф с теми же вершинами, что и граф G и теми ребрами, которые необходимо добавить графу G, чтобы получился полный граф.

Пример:

G:

Матрица смежности дополнительного графа находится по формуле:

A () = J – A (G)

где J – матрица смежности полного графа, состоящая полностью из единиц, за исключением элементов диагонали.

Определение: Двудольным графом G = (V, X) называется граф, вершины которого разбиты на два пересекающихся класса, т. е.: V = V₁V₂, V₁∩V₂ = Ø, а ребра связывают вершины только из разных классов – не обязательно все пары.

Определение: Если в двудольном графе каждая из вершин класса V₁ связана с каждой из вершин класса V₂, то граф называется полным двудольным и обозначается K_m,n , где m – количество вершин первого класса (множество V₁), n – количество вершин второго класса (V₂). Граф K_m,n содержит (m + n) вершин и m·n ребер.

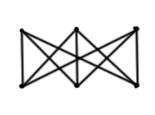
К_3,2 K_3,3 Двудольный

Определение: Пусть G = (V, X) V = {v₁,v₂…,v_n}. Если вершины графа имеют одинаковую степень δ(v_i) = s для всех i { 1, 2, …, n}, то такой граф называется однородным (регулярным).

Теорема 1: Пусть дан однородный граф G = (V, X), V = {v₁,v₂…,v_n}, тогда:

δ(v_i) = n·s;

где n – количество вершин; m – количество ребер; s – степень каждой вершины.

Полный граф является однородным.

Теорема 2: Степень каждой вершины полного графа K_n на 1 меньше числа вершин, т. е. s = n – 1

Теорема 3: Если полный граф имеет n вершин, то

Для однородного графа G матрицы смежности и инцидентности связаны соотношением:

A(G) = B(G)· B^T(G) – s·E, где

B^T(G) – транспонированная матрица инцидентности B(G);

s – степень вершины v однородного графа;

Е – единичная матрица.

Определение: Граф G_p называется реберным, если в качестве вершин его выбраны ребра исходного графа G с m ребрами и n вершинами, имеющего матрицу инцидентности B(G).

В этом случае матрица смежности реберного графа находится по формуле: A (G_p) = B^T(G) · B(G) – 2E

Исходный граф G для построения реберного графа G_p необязательно должен быть регулярным. Если все же граф G является регулярным, то и реберный G_p тоже будет регулярным. В общем случае, если ребро x_i в графе G ограничено вершинами v_j и v_k , степень которых равна δ(v_j) и δ(v_k) , то степень вершины x_i в реберном графе G_p определяется по формуле:

δ(x_i) = δ(v_j) + δ(v_k) – 2

Число ребер в реберном графе G_p определяется по формуле:

m’ = δ²(v_i) – m = δ(x_i)