Геометрическое распределение

Производящая функция распределения P(X = k) = p_k = q^kp, k = 0, 1, … и ее производные при z = 1:

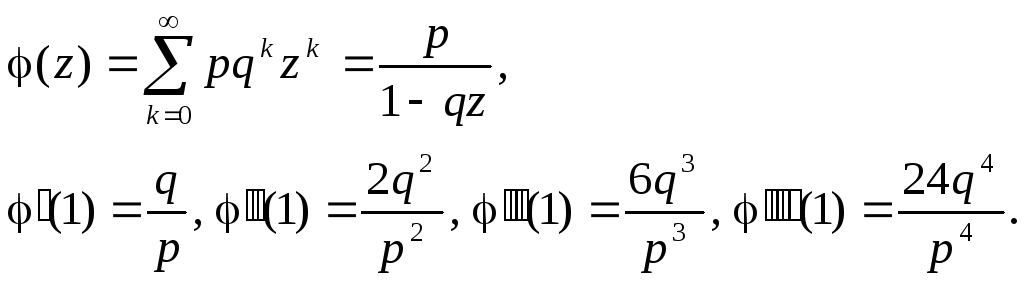
Используя соотношения (4.17) – (4.19), (4.21), получим моментные ЧХ:

Сдвинутое геометрическое распределение

Распределение P(Y = k) = q^k –1p, k = 1, 2,…отличается от геометрического тем, что его возможные значения увеличены на 1 по сравнению с геометрическим распределением X: Y = X + 1. Cогласно свойствам МО и дисперсии

M[Y] = M[X +1] = M[X] +1 =, D[Y] = D[X +1] = D[X] = .

(4.30) (4.31)

Расход снарядов до певого попадания или израсходования боекомплекта

Пока в запасе остается хотя бы один снаряд (из n), вероятность того, что будет израсходовано k снарядов, такая же, как и в сдвинутом геометрическом распределении: P(Z = k) = q^k –1p, k = 1, 2,…, n –1. Событие (Z = n) наступает, если попадание не произошло в n –1 выстрелах:  . Средний расход снарядов и дисперсию определим согласно общим формулам:

M[Z] = ,

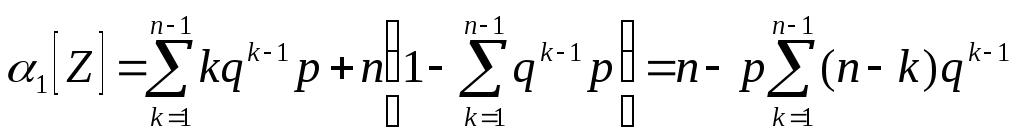D[Z] =

Вычислим МО и дисперсию при p = 0,2 и нескольких значениях n от 1 до 30, чтобы сравнить их с теми же характеристиками бесконечного распределения по формулам (4.30), (4.31) M[Y] = 1/p = 5, D[Y] = q/p² = 0,8/0,04 = 20:

>> p=0.2;q=1-p; N=[1,2,5:5:30];m=[];for n=N k=1:n-1;m(end+1)=n-p*dot(n-k,q.^(k-1));end

>> a=[];for n=N k=1:n-1;a(end+1)=n^2-p*dot((n^2-k.^2),q.^(k-1));end, N,m,D=a-m.^2

N = 1 2 5 10 15 20 25 30

m = 1.0000 1.8000 3.3616 4.4631 4.8241 4.9424 4.9811 4.9938

D = 0 0.1600 2.5700 9.5112 14.867 17.7485 19.0741 19.6348

Результаты показывают, что при достаточно большом боезапасе n > 20 средний расход снарядов в стрельбе до первого попадания можно вычислять по формуле (4.30). Дисперсия ограниченного распределения, естественно, меньше, чем вычисленная по формуле (4.31).

Гипергеометрическое распределение

В предыдущей лекции было показано, что при определенных условиях гипергеометрическое распределение почти не отличается от биномиального. Следовательно, ЧХ этого распределения при тех же условиях можно вычислять по формулам, выведенным для биномиального распределения.

Проверим правильность этого утверждения в условиях выборки из большой и малой партии, сравнив результаты непосредственного вычисления МО и дисперсии с помощью электронной формулы Sampling:

>>N=1000;R=100;M=20;k=0:M;P=Sampling(N,R,M,k);m=sum(P.*k), D=sum(P.*(k-m).^2)

m = 2.0000 D = 1.7657

>> N=50;R=5;P=Sampling(N,R,M,k);m=sum(P.*k), D=sum(P.*(k-m).^2)

m = 2.0000 D = 1.1020

В первом случае n = 20 раз повторяется выбор из большого числа (N = 1000) изделий с практически одинаковой вероятностью p = 100/1000 = 0,1 выбрать бракованное. В условиях испытаний Бернулли с такими параметрами среднее число бракованных изделий в контрольной партии составляло бы np = 200,1 = 2, дисперсия – npq = 200,10,9 = 1,8, что практически совпадает с вычисленными значениями тех же ЧХ по гипергеометрическому распределению. В случае большого отличия между многоугольниками истинного распределения и биномиального приближения (при малом объеме партии N = 50) МО, тем не менее, не изменилось, но истинная дисперсия оказалась существенно меньше, что согласуется с характером различия многоугольников распределения на рис. 3.4: симметрично уменьшились вероятности отклонений от среднего значения.