Начальные и центральные моменты

МО и дисперсия отражают наиболее важные свойства распределений, но используются и другие характеристики, определяемые через математические ожидания целых степеней СВ. Начальным моментом k-о порядка СВ X называется МО k-й степени X:

(4.7)

Центральным моментом k-о порядка СВ X называется МО k-й степени центрированной СВ X:

(4.8)

Асимметрия распределения

Dсе центральные моменты нечетных порядков равны нулю для симметричных распределений, у которых одинаковые противоположные отклонения от m_x равновероятны. Так как ₁[X]  0 для любых распределений, в качестве меры асимметрии принимается ₃[X], точнее, безразмерная величина As – скошенность или асимметрия СВ X:

(4.9)

Эксцесс распределения

Центральный момент четвертого порядка характеризует «островершинность» распределения по сравнению с нормальным законом распределения, у которого безразмерная величина равна 3. Характеристику «островершинности» («крутости») эксцесс вычисляют по формуле:

Ex = – 3.

(4.10)

Все перечисленные ЧХ называются интегральными или моментными, они определяются через соответствующие начальные и центральные моменты. Еще две ЧХ выделяют характерные значения СВ, так называемые характеристики положения – мода (Mo) и медиана (Me).

Мода

Мода дискретной СВ – это ее наиболее вероятное значение: Mo = x_k, если p_k  p_i, i. Мода непрерывной СВ доставляет максимум функции плотности распределения: f(Mo)  f(x), x. Функция плотности f(x) может иметь один или несколько максимумов, может иметь минимум или быть постоянной. Соответственно распределение может быть унимодальными, полимодальным, антимодальным или немодальным.

Медиана

Медиана СВ – такое ее возможное значение Me, что события (X < Me) и (X > Me) равновероятны. Если СВ непрерывна, F(Me) =1/2, но в общем случае медиана обладает свойством F(Me)  1/2, F(Me+0) 1/2, так как P(X < Me) P(X > Me) + P(X = Me), если медиана приходится на точку разрыва функции распределения. У непрерывных симметричных распределений мода, медиана и МО совпадают Mo = Me = m_x = arg F(1/2).

По такой схеме вычисляются все моментные характеристики. Медиана смешанных с.в. имеет следующий смысл F(Me)  1/2, F(Me + 0)  1/2.

Срединное (вероятное) отклонение

Вообще, значение x_p (0 < x_p < 1), для которого выполняется F(x_p)  p, F(x_p + 0)  p, называется квантилью порядка p (медиана – квантиль порядка 1/2). Величина E = (x_3/4 – x_1/4)/2 называется срединным (вероятным) отклонением и принимается иногда за характеристику разброса случайной величины. В отличие от СКО, которое не для всех распределений существует (определенный интеграл в выражении для второго центрального момента может оказаться несобственным), квантиль, а значит и срединное отклонение, можно получить всегда.

Пример

Еще один пример использования квантилей – установление зоны разлета ПЭ в меридиональной плоскости по результатам испытаний в щитовой мишенной обстановке. Отдельные пробоины в направлениях, близких к осевым, не учитываются, границами зоны разлета считаются квантили углового распределения порядков p и 1 – p при достаточно большом p. Например, в интервале [x_0.05, x_0.95] содержится 90% всех фрагментов. За медиану поля разлета принимается угол конуса, который делит область разлета на части, содержащие по половине зачетных фрагментов (квантиль x_0.5).

Статистическое моделирование случайных направлений радиального разлета и построение гистограммы распределения в 2-градусных зонах выполним следующей командой:

>> N=5000;A=180/pi*abs(randn(1,N)*pi/12+75;x=1:2:180;H=hist(A,x)/N;bar(x,H)

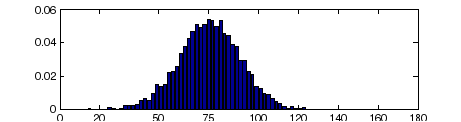
Рис. 4.1. Гистограмма распределения углов разлета

Убедимся, что сумма частот во всех разрядах гистограммы равна единице:

>> sum(H,2)

ans = 1.0000

Найдем 5-процентный и 95-процентный квантили:

>> S=0;i=0; while S<0.05 i=i+1;S=S+n(i); end, fi1=i*2-2

fi1 = 50

>> S=0;i=0; while S<0.05 i=i+1;S=S+n(end-i); end, fi2=180-i*2

fi2 = 100

Найдем медиану углов разлета:

>> S=0;i=0; while S<0.5 i=i+1;S=S+n(i); end, Me=i*2-3

Me = 75