4.4.2. Потенціальна енергія силового поля

Розглянемо деяку скалярну функцію обернену за знаком функції . Тобто . Така функція при умові, що вона є двічі неперервно диференційованою за її аргументами, називається потенціальною енергією. Згідно з (4.22) маємо:

.

(4.25)

Елементарна робота в цьому випадку:

(4.26)

дорівнює повному диференціалу потенціальної енергії, взятому зі знаком мінус. Тоді повна робота на кінцевій ділянці траєкторії точки М :

,

(4.27)

де П₁ і П₂ – значення потенціальної енергії і початковій і кінцевій точках переміщення.

Для визначення потенціальної енергії проінтегруємо рівняння (4.26) в межах від деякого початкового положення М₀ точки до її поточного положення М₁:

.

(4.28)

Стала інтегрування , де - початкове значення потенціальної енергії, яке відповідає знаходженню матеріальної точки в положенні М₀. Стала С залежить від того, яка точка поля обрана за «нульову» для потенціальної енергії. Приймемо, що =0. Тоді з (4.28) виходить:

(4.29)

Таким чином, потенціальна енергія дорівнює роботі, яка здійснюється при переміщенні матеріальної точки із заданого положення у вихідне (початкове), де потенціальна енергія вважається рівною нулю.

Для системи “n” матеріальних точок потенціальна енергія визначається функцією координат //, для якої

.

(4.30)

Тут - проекції сили , що діє на k-ту матеріальну точку. Елементарна робота всіх сил:

.

(4.31)

4.4.3. Закон збереження механічної енергії

Теорему про зміну кінетичної енергії системи матеріальних точок можна записати у вигляді:

.

Якщо всі зовнішні і внутрішні сили, що діють на систему, є потенціальними, то . Тому :

,

або після інтегрування в межах переміщення системи

.

(4.32)

З останнього виходить, що при русі в потенціальному силовому полі сума кінетичної і потенціальної енергії є сталою величиною.

Цю суму називають повною механічною енергією Е матеріальної системи:

.

(4.33)

4.4.4. Узагальнені координати, швидкості і сили

Положення механічної системи, яка складається з “n” матеріальних точок, визначається декартовими координатами. Якщо на систему накладені в’язі, що обмежують рух цієї системи, то визначити її положення можна меншою кількістю координат. Припустимо, що на систему накладено голономних (в’язі, які обмежують тільки положення але не швидкості точок системи) стаціонарних утримуючих в’язей.

Тоді число незалежних координат, за допомогою яких можна визначити положення системи, буде дорівнювати . При розв’язанні інженерних задач для визначення положення механічної системи замість декартових координат часто використовують інші геометричні параметри (кути, довжини, площі, криволінійні координати), що мають різні розмірності.

Будь-які незалежні між собою параметри, які однозначно визначають положення механічної системи, називаються узагальненими координатами цієї системи і позначаються літерою q.

Кількість узагальнених координат співпадає з числом незалежних декартових координат і визначає число ступенів вільності системи m:

.

(4.34)

Рівняння

.

(4.35)

являють собою кінематичні рівняння руху механічної системи в узагальнених координатах.

Приклад: Розглянемо кривошипно-повзунний механізм, положення якого визначається положенням його точок О, А, В, тобто шістьма координатами: .

На систему накладено 5 обмежень (в’язей), рівняння яких мають вигляд:

; .

Тому незалежною буде тільки одна координата з шести. За узагальнену координату можна прийняти будь-яку з трьох: , але зручніше взяти кут повороту кривошипа, оскільки через нього легко виразити всі інші координати.

Для характеристики руху системи користуються поняттям узагальненої швидкості, якою називають похідну за часом від відповідної узагальненої координати:

.

(4.36)

Число узагальнених швидкостей дорівнює числу узагальнених координат системи.

Положення механічної системи, що складається з “n” матеріальних точок і має “т” ступенів вільності визначається узагальненими координатами. Тоді радіус-вектор кожної точки системи буде функцією цих узагальнених координат:

.

Нехай за час точки системи здійснили переміщення . Очевидно, що сума елементарних робіт сил, прикладених до системи з ідеальними в’язями, на цих переміщеннях буде дорінвювати:

.

Розглянемо диференціал радіуса-вектора точки як функцію узагальнених координат:

.

Тоді вираз для елементарних робіт набуває вигляду:

,

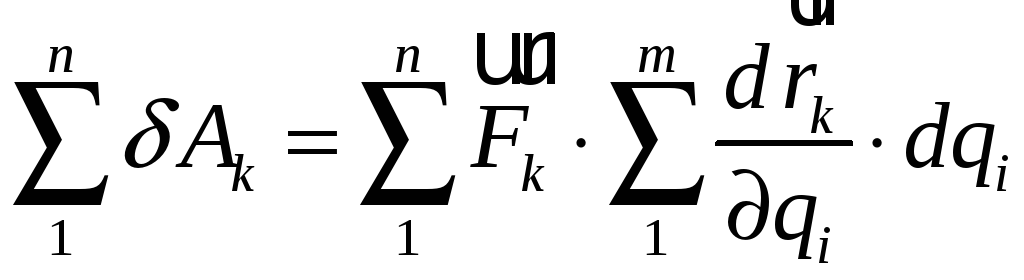або, після зміни порядку підсумовування,

.

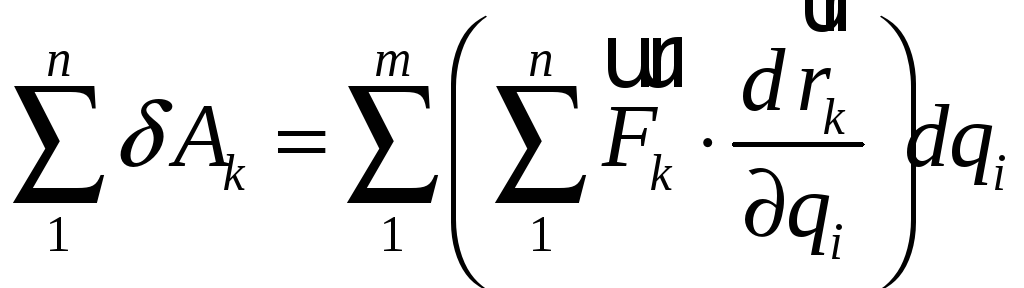Величину, що стоїть в круглих дужках, називають узагальненою силою, яка відповідає і-й узагальненій координаті (позначається через Q_i). Тобто:

.

(4.37)

З урахуванням останнього співвідношення вираз для суми елементарних робіт сил системи запишеться так:

.

(4.38)

Для визначення узагальненої сили , яка відповідає узагальненій координаті , надамо механічній системі таке переміщення, щоб при цьому змінилася тільки координата , а всі інші узагальнені координати залишилися б без змін. Тоді ; . На даному переміщенні сума елементарних робіт всіх активних сил системи, як виходить з рівняння(4.38),

,

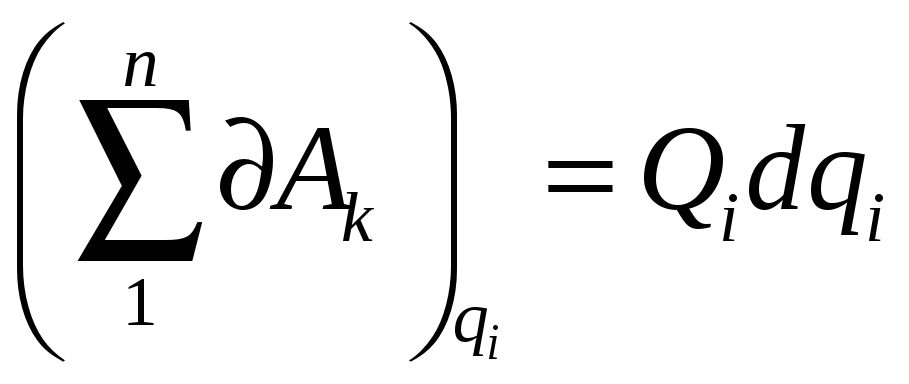звідкіля :

.

(4.39)

В цій формулі індекс при сумі робіт показує, що робота здійснюється тільки на переміщеннях системи, які викликані зміною координати .

За формулою (4.39) і визначають узагальнені сили послідовно даючи нескінченно малі прирісти всім узагальненим координатам.

На основі цієї ж формули можна отримати і розмірність узагальненої сили:

.

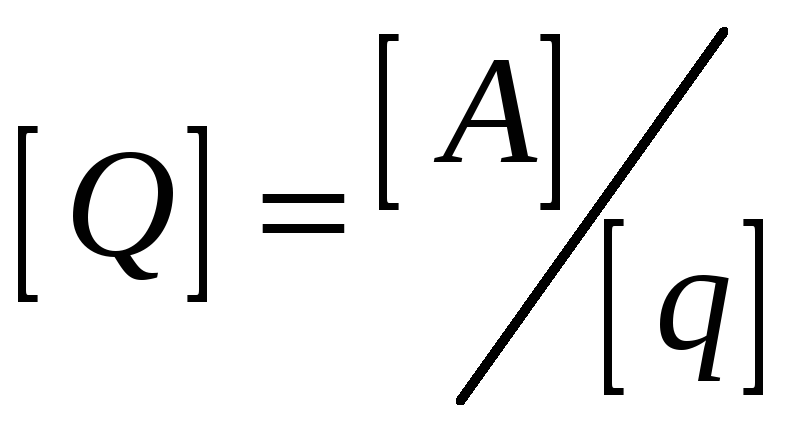Так, якщо узагальнена координата має розмірність довжини, то узагальнена сила має розмірність сили /Н/, якщо ж узагальненою координатою є кут, то узагальнена сила має розмірність момента сили /Н∙м/.

Другий метод визначення узагальнених сил використовують в тому випадку, коли всі сили що діють на механічну систему, є потенціальними (маємо так зване консервативне силове поле).

Тоді: 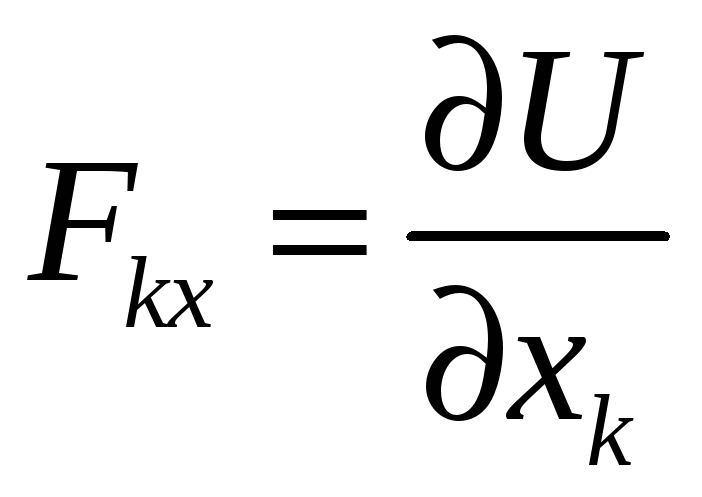; ; 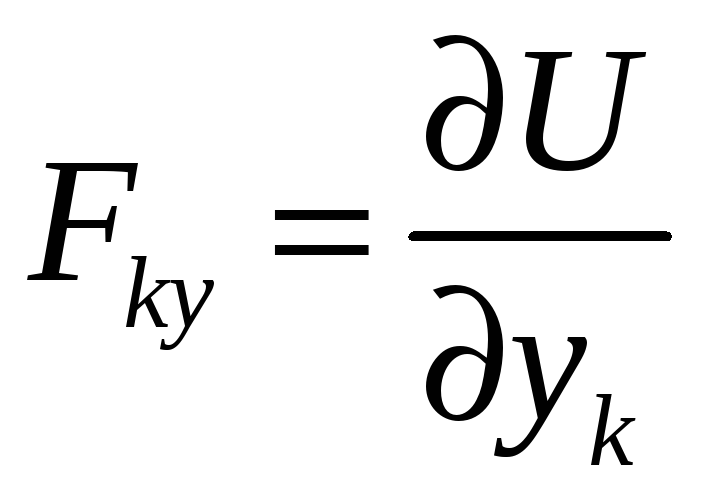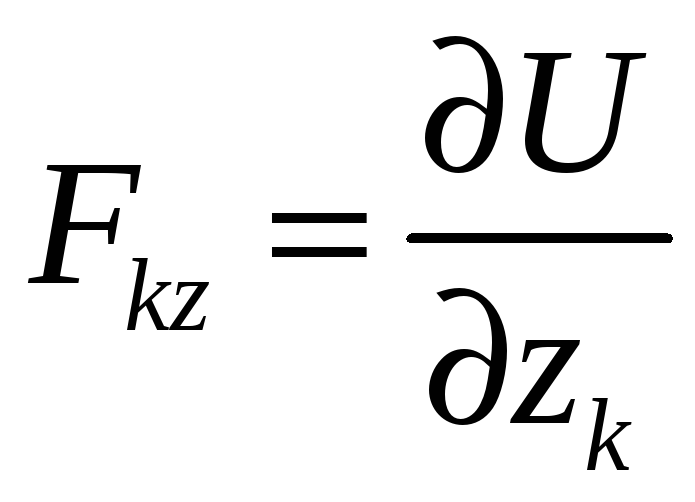, де - силова функція системи.

Підставимо значення проекцій сил у формулу (4.37):

.

(4.40)

Так як , де П – потенціальна енергія системи, то

.

(4.41)

Приклад.

В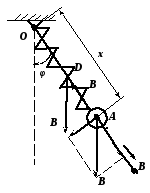изначити узагальнені сили системи, що складається з вантажу А масою , надітого на однорідний стержень ОВ довжиною і масою . Вантаж, зв’язаний з нерухомою точкою О пружиною жорсткістю С (довжина пружини в недеформованому стані дорівнює а), може ковзати вздовж стержня, який коливається у вертикальній площині навколо осі О. Масою пружини і силами тертя нехтувати.

Розв’язання:

Система має два ступені вільності. За узагальнені координати приймаємо кут φ і відстань х вантажу від осі О: , . Зображуємо систему в довільному положенні і прикладемо до неї активні сили: , і силу пружності . Причому реакцію пружини, як реакцію ідеальної в’язі, розглядаємо як активну силу. Дамо координаті φ приріст в бік її збільшення; координату залишаємо без зміни. Підраховуємо суму робіт активних сил на цьому переміщенні:

,

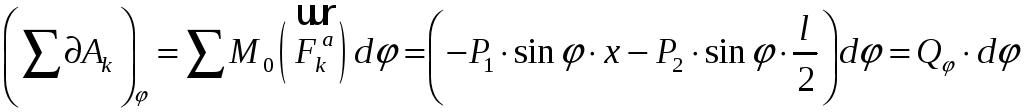звідкіля: .

Змінимо тепер координату х на при .

Тоді

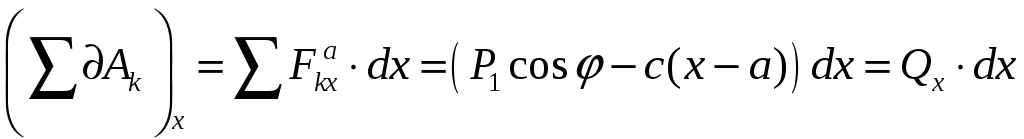
і .

В даному прикладі сили, що діють на систему, потенціальні. При цьому силова функція пружної сили дорівнює , а сили тяжіння . Якщо вісь напрямити з точки вверх, то силова функція системи запишеться у вигляді:

,

( і )

і вирази узагальнених сил знаходяться за формулою (4.40):

;

.

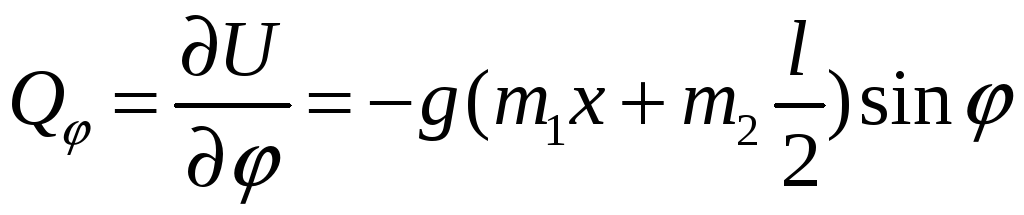Результати співпадають.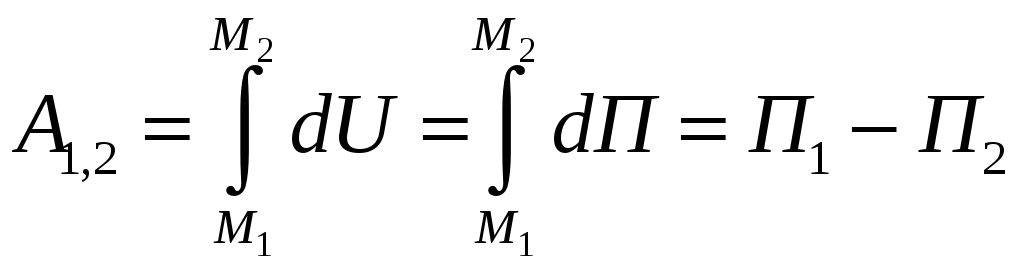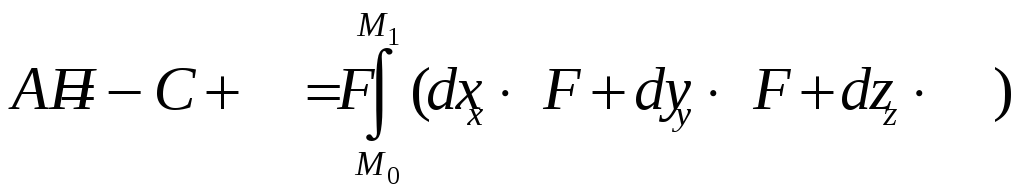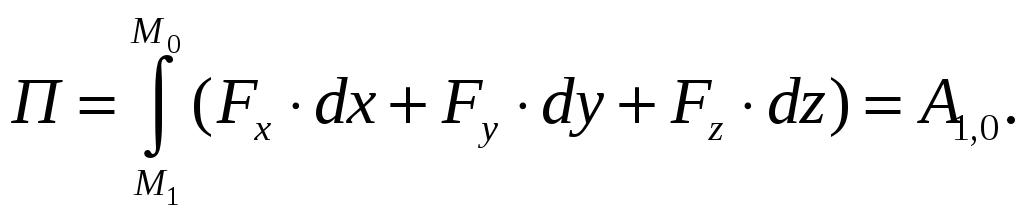
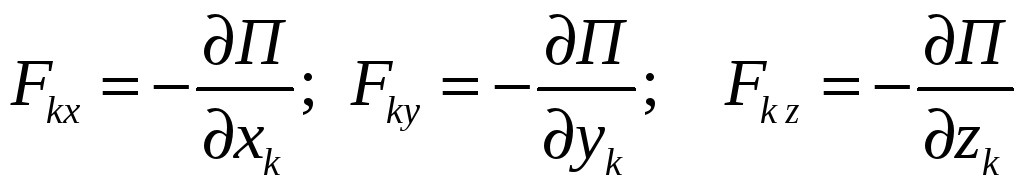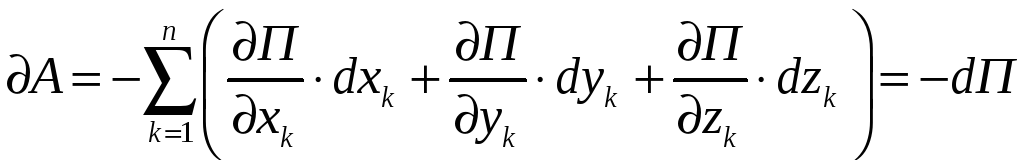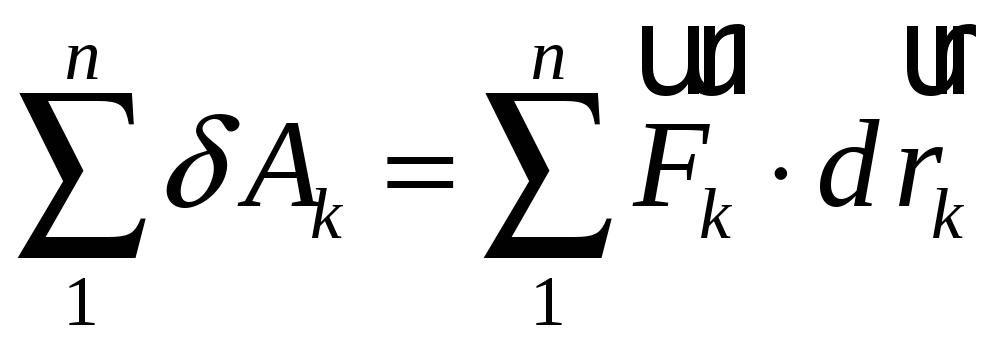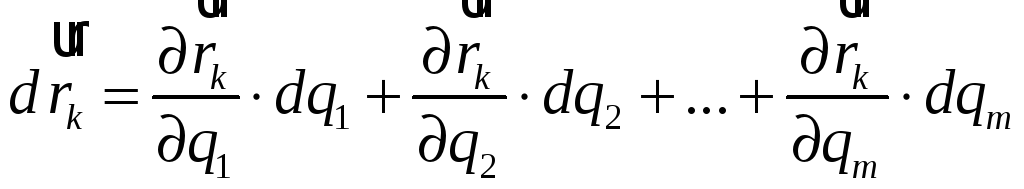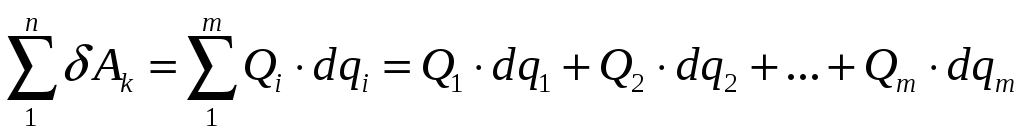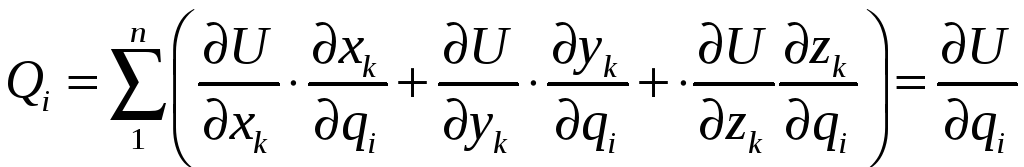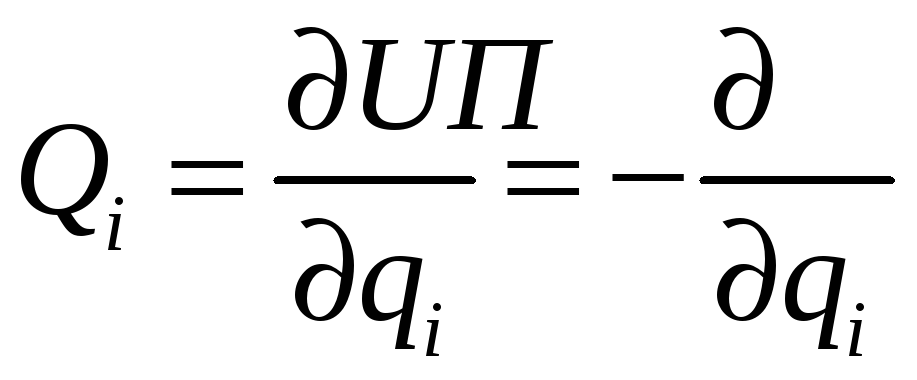