Практическая часть Задачи

Задача 1.

Найти наибольшее и наименьшее значения функции при:

Задача 2.

Найти наибольшее и наименьшее значения функции при:

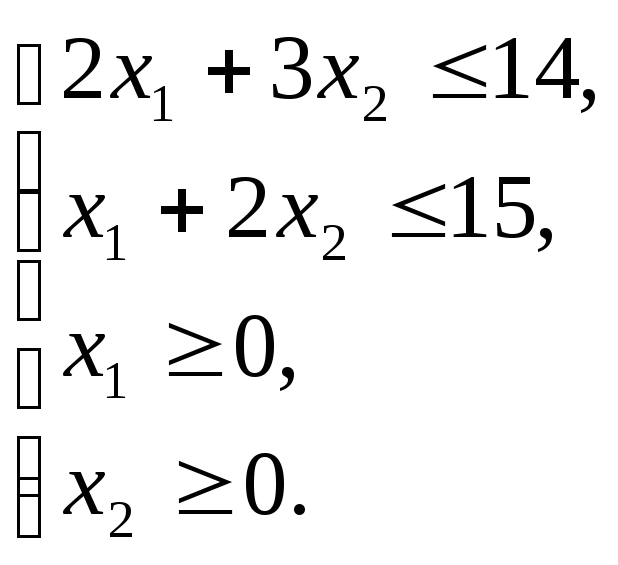
Задача 3.

Найти точки экстремума функции при условии, что .

Задача 4.

Найти наибольшее и наименьшее значение функции при:

Решения

Задача 1.

О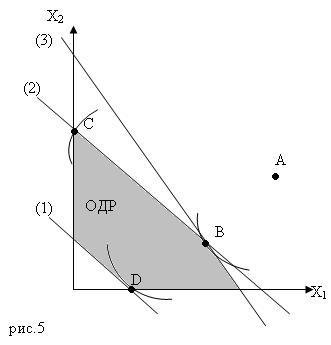бластью допустимых решений системы неравенств является выделенный многоугольник (рис.5), построенный по координатам, данным ниже:

(1)

x1		0	2
x2		1	0

x1	0	6
x2	6	0

x1	0	5.5
x2	11	0

(2) (3)

Полагая значения целевой функции равным некоторому числу , получаем линии уровня, а именно окружности

С центром A(7;3) и радиусом . С увеличением (уменьшением) числа значения функции Z соответственно увеличиваются (уменьшаются).

Проводя из точки A окружности разных радиусов, видим, что минимальное значение целевая функция принимает в точке B, в которой окружность касается области решений.

Для определения координат этой точки воспользуемся равенством угловых коэффициентов прямой и касательной к окружности в точке B. Из уравнения прямой следует, что ее угловой коэффициент равен . Для нахождения углового коэффициента касательной

берем уравнение окружности и, рассматривая как неявную функцию переменной , дифференцируем уравнение окружности отсюда .

Приравнивая найденную производную числу, получаем одно из уравнений для определения координат точки B. Присоединяя к нему уравнения прямой, на которой лежит точка B, имеем систему:

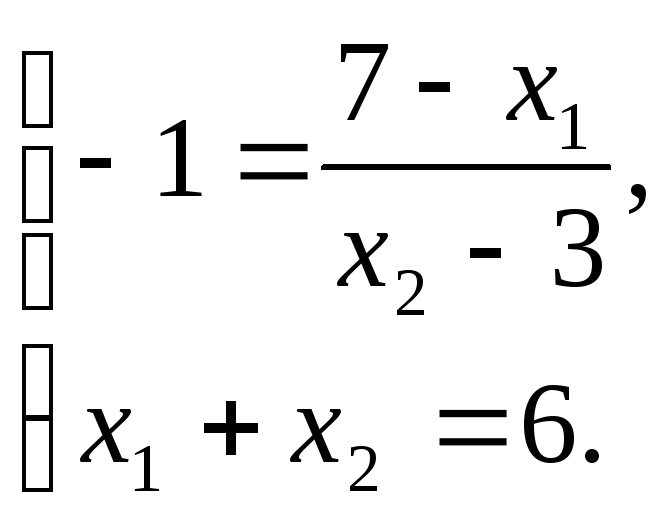
Откуда т.е. B(5;1).

Таким образом,

Из рис. 5 видно, что координаты точки C(0;6), а точки D(2;0). Максимальное значение функции Z будет в точке С(0;6) и при этом

.

Задача 2.

О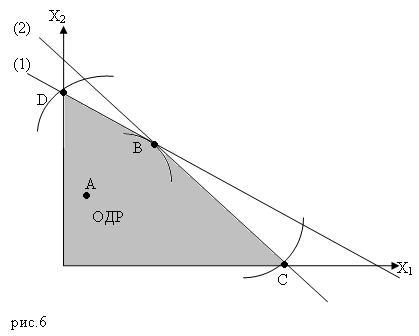бластью допустимых решений системы неравенств выделенный является многоугольник (рис.6), построенный по координатам, данным ниже:

(1)

x1	0	12
x2	8	0

(2)

x1	0	15
x2	7,5	0

Представим целевую функцию Z в виде суммы квадратов, полагая значения Z равным некоторому числу .Представим :

получаем линии уровня, а именно окружности

С центром A(1;3), лежащей в области допустимых решений и являющейся минимальным значением целевой функции, и радиусом . С увеличением (уменьшением) числа значения функции Z соответственно увеличиваются (уменьшаются).

Проводя из точки A окружности разных радиусов, видим, что максимальное значение целевая функция принимает в точке С, в которой окружность касается области решений.

Для определения координат точки B воспользуемся равенством угловых коэффициентов прямой и касательной к окружности в этой точке. Из уравнения прямой следует, что ее угловой коэффициент равен. Для нахождения углового коэффициента касательной берем уравнение окружности и, рассматривая как неявную функцию переменной , дифференцируем уравнение окружности отсюда .

Приравнивая найденную производную числу, получаем одно из уравнений для определения координат точки B. Присоединяя к нему уравнения прямой, на которой лежит точка B, имеем систему:

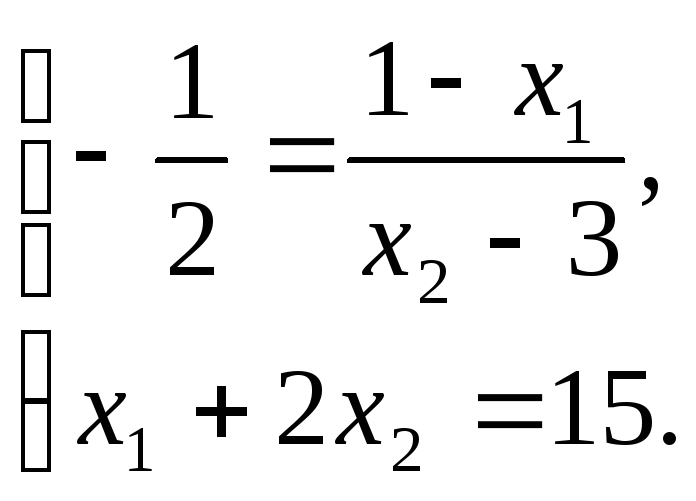
Откуда т.е. B(2,6;6,2).

Из рис. 6 видно, что координаты точки C(12;0), а точки D(0;8).

Максимальное значение функции Z будет в точке С(12;0) и при этом

Задача 3.

Составим функцию Лагранжа .

Найдем ее частные производные по , приравнивав их к нулю:

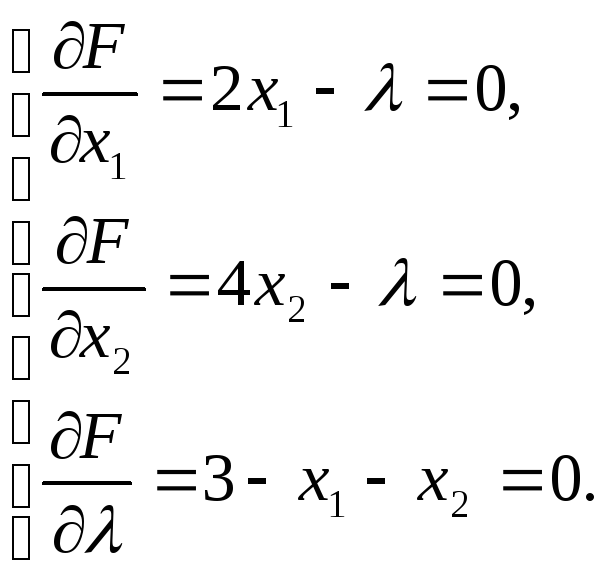
Решение системы . Таким образом, в точке данная функция может иметь условный экстремум. Найдем .

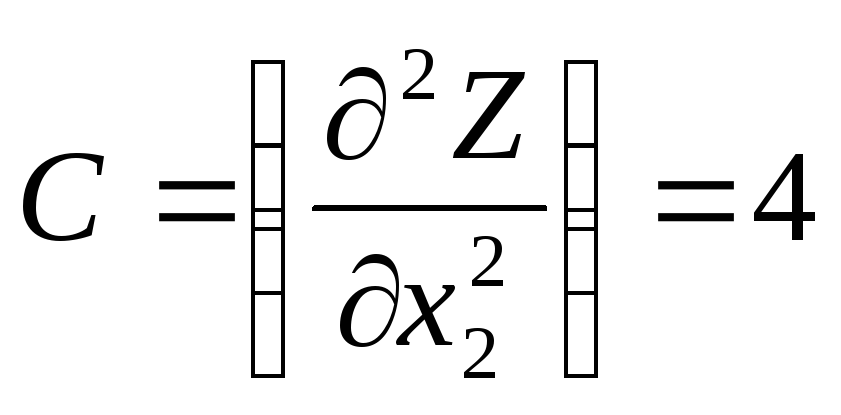Так как и , то в точке имеем условный минимум, причем .

Задача 4.

Найдем частные производные по :

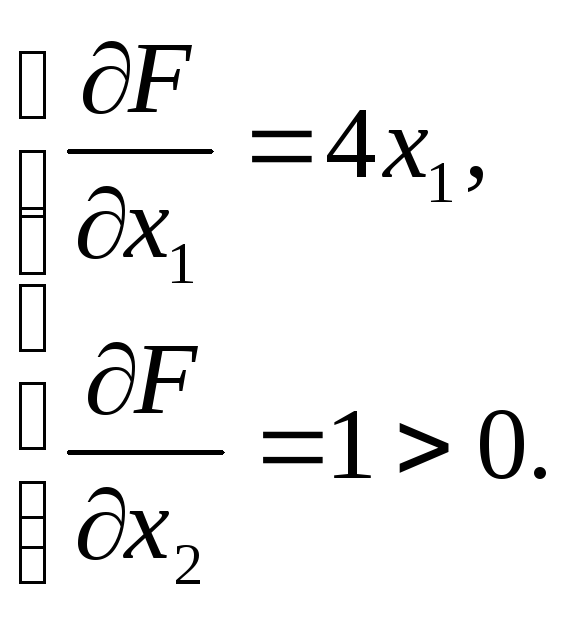
Условие (a)

- не подходит;

Условие (b)

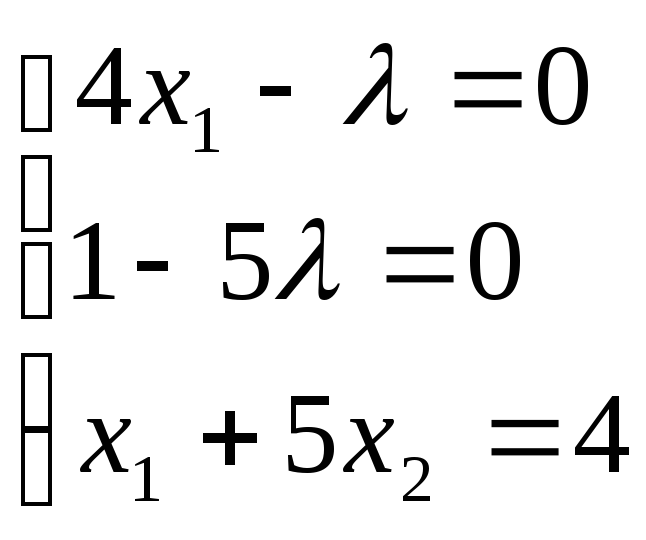
- подходит;

Условие (c)

- не подходит;

Условие (d)

- не подходит;

В точке О имеем условный минимум, причем , но указать глобальный минимум нет возможности.