Критерии оптимальности в задачах с ограничениями.

Ряд инженерных задач связан с оптимизацией при наличии некоторого количества ограничений на управляемые пере­менные. Такие ограничения существенно уменьшают размеры об­ласти, в которой проводится поиск оптимума. На первый взгляд может показаться, что уменьшение размеров допустимой области должно упростить процедуру поиска оптимума. Между тем, напро­тив, процесс оптимизации становится более сложным, поскольку установленные выше критерии оптимальности нельзя использовать при наличии ограничений. При этом может нарушаться даже ос­новное условие, в соответствии с которым оптимум должен достигаться в стационарной точке, характеризующейся нулевым гра­диентом. Например, безусловный минимум функции имеет место в стационарной точке х=2. Но если задача минимиза­ции решается с учетом ограничения , то будет найден условный минимум, которому соответствует точка x=4. Эта точка не является стационарной точкой функции f, так как (4)=4. Далее исследуются необходимые и достаточные условия оптимальности решений задач с ограничениями.

Графическое решение задач нелинейного программирования

Существующие методы нелинейного программирования применимы лишь при известных предположениях о характере ограничений и целевой функции задачи.

Система ограничений (2) отделяет область допустимых решений. В отличие от задачи линейного программирования она не всегда является выпуклой. Даже если область допустимых решений является выпуклой, то в ряде задач целевая функция может иметь несколько локальных экстремумов. С помощью большинства же вычислительных методов можно найти точку локального оптимума, но нельзя установить, является ли она точкой глобального (абсолютного) оптимума или нет.

Н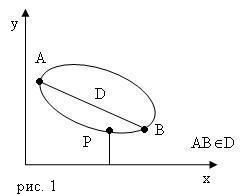а рис.1 показана выпуклая область (круг, шар, куб) для нее отрезок ABD, а точка P является точкой абсолютного минимума. Для невыпуклой области (рис.2) отрезок ABD целиком. Точки M и N являются точками минимума, но для области D точка N точкой абсолютного минимума не является. Поэтому будем говорить, что в точке M достигается глобальный минимум, а в точке N достигается локальный минимум.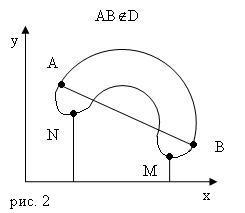

В задачах нелинейного программирования точка экстремума может лежать в вершине многогранника, на ребре (грани) или внутри области. Если задача содержит нелинейные ограничения, то область допустимых решений не является выпуклой и кроме глобального оптимума могут существовать точки локального оптимума. Для того чтобы при решении задач нелинейного программирования имелась уверенность, что полученный оптимальный план отвечает именно глобальному оптимуму, достаточно, чтобы область допустимых решений была выпуклой, а целевая функция – вогнутой (для задач на max) или выпуклой (для задач на min). Экономические задачи очень часто отвечают этим условиям.

Процесс нахождения решения задач нелинейного программирования (1) и (2) с использованием ее геометрической интерпретации включает следующие этапы:

1. Находят область допустимых решений задачи, определяемую соотношениями (2) (если она пуста, то задача не имеет решений);

2. Строят гиперповерхность 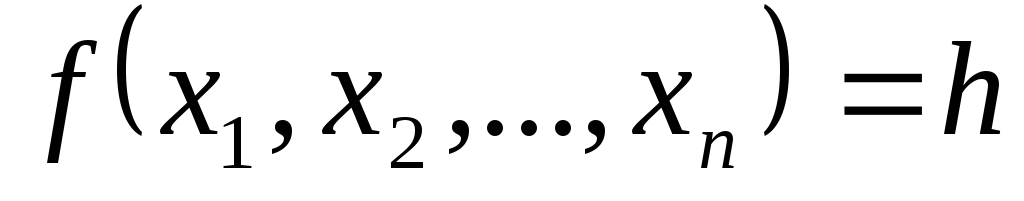(гиперповерхность – обобщение понятия поверхности 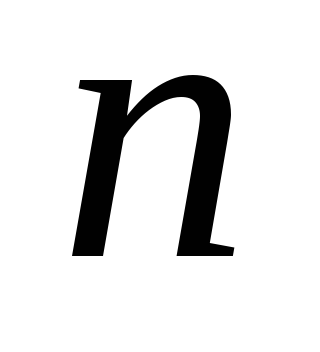–го порядка – гиперплоскость);

3. Определяют гиперповерхность наивысшего (наинизшего) уровня или устанавливают неразрешимость задачи из-за неограниченности функции (1) сверху (снизу) на множестве допустимых решений;

4. Находят точку области допустимых решений, через которую проходит гиперповерхность наивысшего (наинизшего) уровня, и определяют в ней значение функции (1).

Пример 1.

Найти минимальное и максимальное значения функции

При ограничениях

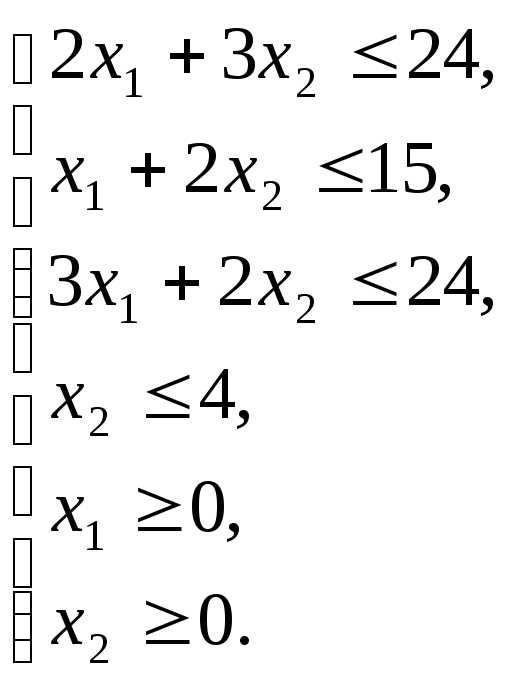
Н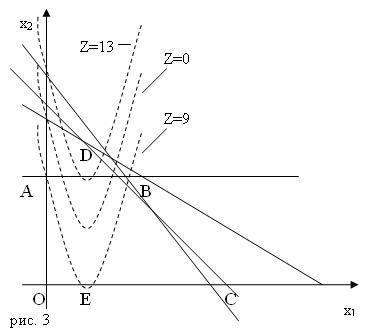аходим область допустимых решений – многоугольник OABC (рис. 3)

Строим линию уровня

где - некоторая постоянная и исследуем ее поведение при различных значениях . Преобразуем линию уровня .

При каждом значении получаем параболу, которая тем выше отдалена от оси OX, чем больше значение .

Значит функция Z принимает оптимальные значения в точке касания одной из парабол с границей многоугольника OABC.

Минимальное значение в точке E:

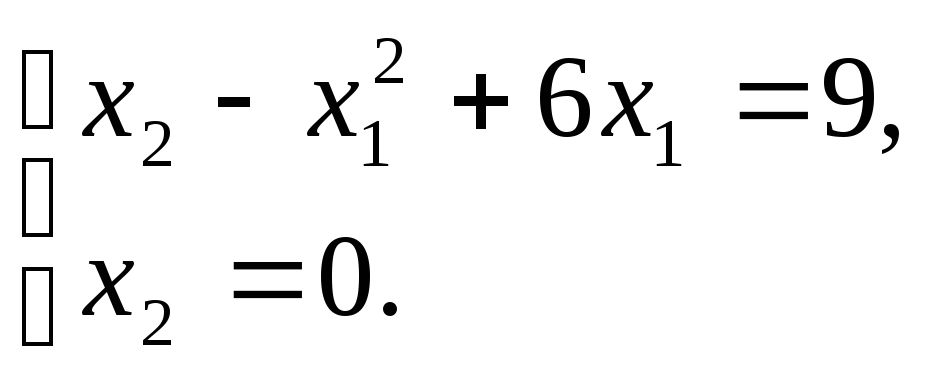
Решая эту систему, найдем, что , т.е в точке E (3;0).

Максимальное значение в точке D:

Отсюда и в точке D(3;4).

Точки, соответствующие оптимальным значениям функции Z не являются вершинами многоугольника допустимых решений. Поэтому процедура перебора вершин, которая использовалась при решении задач нелинейного программирования, неприменима для решения данной задачи.

Пример 2.

Найти максимальное и минимальное значение функции

При условиях

Областью допустимых решений системы неравенств является многоугольник OABC (рис.4).

Полагая значения целевой функции равным некоторому числу , получаем линии уровня ,а именно окружности

С центром M(1;5) и радиусом . С увеличением (уменьшением) числа значения функции Z соответственно увеличиваются (уменьшаются).

Проводя из точки М окружности разных радиусов, видим, что минимальное значение целевая функция принимает в точке D, в которой окружность касается области решений.

Для определения координат этой точки воспользуемся равенством угловых коэффициентов прямой и касательной к окружности в точке D. Из уравнения прямой следует, что ее угловой коэффициент равен . Для нахождения углового коэффициента касательной берем уравнение окружности и, рассматривая как неявную функцию переменной , дифференцируем уравнение окружности отсюда .

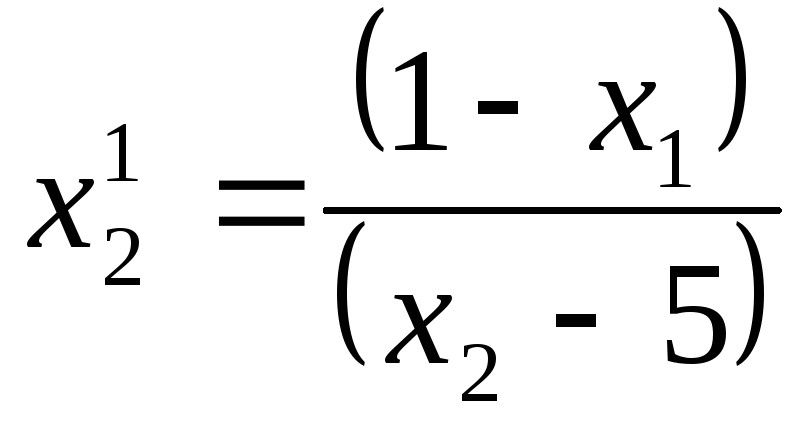Приравнивая найденную производную числу , получаем одно из уравнений для определения координат точки D. Присоединяя к нему уравнения прямой, на которой лежит точка D, имеем систему:

Откуда т.е. D(2;3).

Таким образом,

Из рис. 4 видно, что максимальное значение функции Z будет в точке С(4;0) и при этом Z_max=34.