
- •02 Марта 2009
- •1. Введение
- •2. Точки пересечения физики и топологи
- •2.1. Теоретические основы
- •2.2. Категории
- •2.3. Моноидальные категории
- •2.4. Сплетённые моноидальные категории
- •2.5. Симметричные моноидальные категории
- •2.6. Замкнутые категории
- •3.1. Теоретические основы
- •3.2. Доказательства как морфизмы
- •4. Теория вычислений
- •4.1. Теоретические основы
- •Благодарности
- •Список литературы
4. Теория вычислений
4.1. Теоретические основы
В 1930-х годах, когда А. М. Тьюринг разрабатывал
то, что сейчас называют «машинами
Тьюринга» в качестве модели вычислений,
А. Чёрч и его студент С. Клини вели работы
по созданию другой модели, названной
«![]() -исчисление»
[29, 63]. В то время как машина Тьюринга
представляет собой идеализированную,
упрощённую модель аппаратного
обеспечения компьютеров,
-исчисление»
[29, 63]. В то время как машина Тьюринга
представляет собой идеализированную,
упрощённую модель аппаратного
обеспечения компьютеров, ![]() -исчисление
больше похоже на упрощённую
модель программного обеспечения.
-исчисление
больше похоже на упрощённую
модель программного обеспечения.
На данный момент имеется множество
подробных описаний
![]() -исчисления,
начиная от авторитетного труда Х.
Барендрегта [17] до классического
теоретико-категориального рассмотрения
вопроса Дж. Ламбеком и П. Дж. Скоттом
[67], практичного введения Р. Хиндли и Дж.
П. Селдина [51] и ясно изложенных заметок
П. Селинджера, доступных в Интернете в
режиме он-лайн [86]. Поэтому в данной
работе авторы ограничатся лишь кратким
описанием
-исчисления,
начиная от авторитетного труда Х.
Барендрегта [17] до классического
теоретико-категориального рассмотрения
вопроса Дж. Ламбеком и П. Дж. Скоттом
[67], практичного введения Р. Хиндли и Дж.
П. Селдина [51] и ясно изложенных заметок
П. Селинджера, доступных в Интернете в
режиме он-лайн [86]. Поэтому в данной
работе авторы ограничатся лишь кратким
описанием
![]() -исчисления.
-исчисления.
Образно, ![]() -исчисление
описывает вселенную, в которой всё
является программами и всё является
данными: программы являются данными.
Более прозаически, всё является
«
-исчисление
описывает вселенную, в которой всё
является программами и всё является
данными: программы являются данными.
Более прозаически, всё является
«![]() -термами»
или просто «термами» для краткости.
Термы определяются индуктивно:
-термами»
или просто «термами» для краткости.
Термы определяются индуктивно:
-
Переменные: имеется счётное множество «переменных»
 ,
, 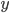 ,
, 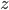 ,
каждая из которых является термом.
,
каждая из которых является термом. -
Применение (аппликация): если
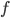 и
и 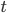 являются
термами, то можно «применить» терм
являются
термами, то можно «применить» терм 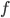 к
терму
к
терму 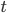 ,
результатом чего является терм
,
результатом чего является терм 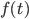 .
. -
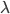 -абстракция:
если
-абстракция:
если 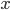 является
переменной, а
является
переменной, а 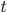 есть
терм, то термом является выражение
есть
терм, то термом является выражение 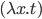 .
.
Необходимо разъяснить значение
аппликации и ![]() -абстракции.
С аппликацией всё просто. Поскольку
«программы являются данными», любой
терм можно трактовать и как программу,
и как данные. Поскольку можно применять
программы к данным для получения новых
данных, то любой терм
-абстракции.
С аппликацией всё просто. Поскольку
«программы являются данными», любой
терм можно трактовать и как программу,
и как данные. Поскольку можно применять
программы к данным для получения новых
данных, то любой терм ![]() ,
к примеру, применим к любому другому
терму
,
к примеру, применим к любому другому
терму ![]() для
получения нового терма
для
получения нового терма ![]() .
.
![]() -абстракция
вызывает больший интерес.
Терм
-абстракция
вызывает больший интерес.
Терм ![]() рассматривается
как программа, которая получает на вход
значение
рассматривается
как программа, которая получает на вход
значение ![]() и
возвращает в качестве результата терм
и
возвращает в качестве результата терм ![]() .
Например, пусть имеется терм
.
Например, пусть имеется терм ![]() .
Данная программа получает на вход
произвольный терм
.
Данная программа получает на вход
произвольный терм ![]() и
возвращает в качестве результата терм
и
возвращает в качестве результата терм ![]() .
Другими словами, он применяет произвольную
программу к самой себе. Так что,
например,
.
Другими словами, он применяет произвольную
программу к самой себе. Так что,
например, ![]() для
произвольного терма
для
произвольного терма ![]() .
.
Более абстрактно, если терм применим к
какому-либо терму ![]() ,
то результатом будет терм
,
то результатом будет терм
![]() ,
в котором все свободные вхождения
переменной
,
в котором все свободные вхождения
переменной ![]() заменены на терм
заменены на терм
![]() ,
что можно записать при помощи правила,
называемого
,
что можно записать при помощи правила,
называемого ![]() -редукцией:
-редукцией: ![]() ,
где
,
где ![]() представляет
собой терм
представляет
собой терм ![]() ,
в котором все свободные вхождения
переменной
,
в котором все свободные вхождения
переменной ![]() заменены
на терм
заменены
на терм ![]() В
оригинале используется запись
В
оригинале используется запись![]() ,
из-за чего сами авторы иногда путаются
в связи с неинтуитивностью обозначения
— прим. перев. . Однако нужно соблюдать
осторожность, поскольку это правило не
является уравнением в математическом
понимании. Это — «правило подстановки»:
если имеется терм, расположенный слева
от знака равенства, то вместо него можно
подставить терм, находящийся справа от
данного знака. Начиная с некоторого
терма при последовательном применении
правил подстановки, происходит выполнение
программы!
,
из-за чего сами авторы иногда путаются
в связи с неинтуитивностью обозначения
— прим. перев. . Однако нужно соблюдать
осторожность, поскольку это правило не
является уравнением в математическом
понимании. Это — «правило подстановки»:
если имеется терм, расположенный слева
от знака равенства, то вместо него можно
подставить терм, находящийся справа от
данного знака. Начиная с некоторого
терма при последовательном применении
правил подстановки, происходит выполнение
программы!
В ![]() -исчислении
имеется два других правила подстановки.
Если
-исчислении
имеется два других правила подстановки.
Если ![]() является
термом, а
является
термом, а ![]() переменной,
то терм
переменной,
то терм ![]() представляет
собой программу, которая для
заданного
представляет
собой программу, которая для
заданного ![]() возвращает
возвращает ![]() .
Но это всего лишь своеобразный способ
записи терма
.
Но это всего лишь своеобразный способ
записи терма ![]() .
Так что в
.
Так что в ![]() -исчислении
имеется правило подстановки,
называемое
-исчислении
имеется правило подстановки,
называемое ![]() -редукцией,
которое записывается как
-редукцией,
которое записывается как ![]() .
.
Третье правило подстановки
называется ![]() -конверсией.
Оно позволяет заменять в термах связанные
переменные. Например:
-конверсией.
Оно позволяет заменять в термах связанные
переменные. Например: ![]() ,
поскольку переменная
,
поскольку переменная ![]() связана
в левом терме с символом
связана
в левом терме с символом ![]() .
Другими словами, всякая переменная
.
Другими словами, всякая переменная ![]() является
лишь обозначением, её наименование не
представляет важности, так что его можно
заменять. Однако, с другой стороны,
является
лишь обозначением, её наименование не
представляет важности, так что его можно
заменять. Однако, с другой стороны, ![]() ,
поскольку переменная
,
поскольку переменная ![]() свободна в левом терме, она не является
связанной и потому не может быть заменена.
Понятию свободных и связанных переменных
стоило бы придать большую ясность,
однако в настоящей статье этот вопрос
будет опущен; авторы отсылают читателя
к указанным ранее источникам для
получения разъяснений.
свободна в левом терме, она не является
связанной и потому не может быть заменена.
Понятию свободных и связанных переменных
стоило бы придать большую ясность,
однако в настоящей статье этот вопрос
будет опущен; авторы отсылают читателя
к указанным ранее источникам для
получения разъяснений.
![]() -исчисление
— это очень простая система. Удивительно
то, что с его помощью А. Чёрч и С. Клини
смогли построить булеву логику,
натуральные числа, обычные арифметические
операции и т. д. Например, они определили
«нумералы Чёрча» следующим образом:
-исчисление
— это очень простая система. Удивительно
то, что с его помощью А. Чёрч и С. Клини
смогли построить булеву логику,
натуральные числа, обычные арифметические
операции и т. д. Например, они определили
«нумералы Чёрча» следующим образом:
и т. д. Необходимо отметить, что
терм ![]() является
переменной. Поэтому что нумерал
Чёрча
является
переменной. Поэтому что нумерал
Чёрча ![]() является
программой, которая «возводит заданную
программу в степень
является
программой, которая «возводит заданную
программу в степень ![]() »:
если задать ей программу
»:
если задать ей программу ![]() в
качестве входного значения, то результатом
будет применение данной программы
в
качестве входного значения, то результатом
будет применение данной программы
![]() раз
к некоторому аргументу
раз
к некоторому аргументу ![]() .
.
Чтобы лучше понять, как можно определить
арифметические операции над нумералами
Чёрча, рассмотрим терм ![]() .
Данный терм принимает на вход некоторую
программу
.
Данный терм принимает на вход некоторую
программу ![]() и
возводит её в квадрат, после чего возводит
результат в куб. Таким образом, он
возводит программу
и
возводит её в квадрат, после чего возводит
результат в куб. Таким образом, он
возводит программу ![]() в
шестую степень, что предполагает:
в
шестую степень, что предполагает:
![]() .
Это так и есть на самом деле. Если
рассматривать определения нумералов
Чёрча в качестве обратимых правил
подстановки, то можно начать с левой
части приведённого выражения и достичь
правой части при помощи применения
правил подстановки:
.
Это так и есть на самом деле. Если
рассматривать определения нумералов
Чёрча в качестве обратимых правил
подстановки, то можно начать с левой
части приведённого выражения и достичь
правой части при помощи применения
правил подстановки:
|
|
|
|
Определение |
|
|
|
|
|
|
|
|
|
Определение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определение |
Несмотря на то, что вычисление кажется
громоздким, это как раз то, что нужно,
поскольку воссоздаёт внутреннюю работу
компьютера. Мы видим, как ![]() -исчисление
может использоваться в качестве языка
программирования, когда каждому шагу
вычислений соответствует применение
правила подстановки.
-исчисление
может использоваться в качестве языка
программирования, когда каждому шагу
вычислений соответствует применение
правила подстановки.
Конечно, ответ ![]() получен
потому, что
получен
потому, что ![]() .
Обобщая данный пример, можно разработать
программу, называемую «
.
Обобщая данный пример, можно разработать
программу, называемую «![]() »,
которая перемножает два заданных
нумерала Чёрча:
»,
которая перемножает два заданных
нумерала Чёрча: ![]() .
Например,
.
Например, ![]() .
Заинтересованный читатель может
самостоятельно разработать термы для
представления других базовых арифметических
операций над нумералами Чёрча. Для
большей ясности стоит отметить, что А.
Чёрч и С. Клини могли записывать термы
для выполнения более сложных функций.
В результате они пришли к пониманию
того, что все вычислимые
функции
.
Заинтересованный читатель может
самостоятельно разработать термы для
представления других базовых арифметических
операций над нумералами Чёрча. Для
большей ясности стоит отметить, что А.
Чёрч и С. Клини могли записывать термы
для выполнения более сложных функций.
В результате они пришли к пониманию
того, что все вычислимые
функции ![]() могут быть определены в терминах
могут быть определены в терминах
![]() -исчисления.
-исчисления.
Тем временем К. Гёдель разработал другой
подход к вычислимости, теорию «рекурсивных
функций». Около 1936-го года С. Клини
доказал, что функции, определимые в
терминах ![]() -исчисления,
являются теми же функциями, что и
рекурсивные функции Гёделя. В 1937-ом году
А.М. Тьюринг описал свои «машины Тьюринга»
и использовал их для иного определения
вычислимых функций. Впоследствии
выяснили, что его определение согласовано
с первыми двумя. На данный момент
вышеупомянутое и другие подтверждения
дают основание полагать, что
-исчисления,
являются теми же функциями, что и
рекурсивные функции Гёделя. В 1937-ом году
А.М. Тьюринг описал свои «машины Тьюринга»
и использовал их для иного определения
вычислимых функций. Впоследствии
выяснили, что его определение согласовано
с первыми двумя. На данный момент
вышеупомянутое и другие подтверждения
дают основание полагать, что
![]() -исчисление
может определить любую функцию,
вычисляемую произвольным систематическим
методом. Говорят, что
-исчисление
может определить любую функцию,
вычисляемую произвольным систематическим
методом. Говорят, что ![]() -исчисление
является полным по Тьюрингу.
-исчисление
является полным по Тьюрингу.
После «всплеска» теоретических разработок
потребовалось ещё несколько десятилетий
для того, чтобы построить компьютеры.
Больше времени заняли попытки практического
применения работ А. Чёрча и С. Клини. Это
произошло около 1958 года, когда Дж.
Маккарти изобрёл язык программирования
Lisp, основанный на
![]() -исчислении
[74]. В 1965 году авторитетная статья П.
Ландина [68] указала на разительное
сходство
-исчислении
[74]. В 1965 году авторитетная статья П.
Ландина [68] указала на разительное
сходство
![]() -исчисления
и языка программирования Algol. Эти открытия
возобновили интерес к
-исчисления
и языка программирования Algol. Эти открытия
возобновили интерес к ![]() -исчислению,
который не утихает до сих пор. На данный
момент несколько языков программирования
полностью основаны на идеях из
-исчислению,
который не утихает до сих пор. На данный
момент несколько языков программирования
полностью основаны на идеях из ![]() -исчисления.
Наиболее известными из них являются
языки Lisp, ML и Haskell. Эти языки, называемые
«функциональными языками программирования»,
обожают теоретики в области компьютерных
наук за их концептуальную чистоту.
Фактически, на протяжении многих лет
каждый обучающийся компьютерным наукам
в Массачусетском технологическом
институте (MIT) должен был пройти вводный
курс с изучением языка Scheme, диалекта
Lisp. На обложке книги курса [1] расположена
большая буква
-исчисления.
Наиболее известными из них являются
языки Lisp, ML и Haskell. Эти языки, называемые
«функциональными языками программирования»,
обожают теоретики в области компьютерных
наук за их концептуальную чистоту.
Фактически, на протяжении многих лет
каждый обучающийся компьютерным наукам
в Массачусетском технологическом
институте (MIT) должен был пройти вводный
курс с изучением языка Scheme, диалекта
Lisp. На обложке книги курса [1] расположена
большая буква ![]() .
.
Необходимо отметить, что языки
программирования другого вида, а именно
«императивные языки программирования»,
более популярны среди работающих
программистов. К таким языкам относятся,
например, Fortran, Basic и C. В императивном
программировании программа представляет
собой набор инструкций, которые говорят
компьютеру, что делать. В функциональных
же языках программа просто описывает
функцию. Для запуска такой программы,
её необходимо применить к входным
данным. Так что, как и в ![]() -исчислении,
«применение» является основной операцией
в функциональном программировании.
Если объединить применение с
-исчислении,
«применение» является основной операцией
в функциональном программировании.
Если объединить применение с ![]() -абстракцией,
то в результате получится язык, достаточный
для выражения любой вычислимой функции.
-абстракцией,
то в результате получится язык, достаточный
для выражения любой вычислимой функции.
Однако следует сказать, что большинство
функциональных языков программирования
более систематизированы, нежели
оригинальное
![]() -исчисление.
Как было показано, в
-исчисление.
Как было показано, в
![]() -исчислении,
разработанном А. Чёрчем и С. Клини, любой
терм может быть применён к любому
другому. В действительности, программирование
использует многие виды данных. Например,
пусть в некоторой программе обрабатываются
дни недели. В ней не будет иметь никакого
смысла выражение
-исчислении,
разработанном А. Чёрчем и С. Клини, любой
терм может быть применён к любому
другому. В действительности, программирование
использует многие виды данных. Например,
пусть в некоторой программе обрабатываются
дни недели. В ней не будет иметь никакого
смысла выражение ![]() ,
поскольку терм
,
поскольку терм ![]() не
является числом. Можно представлять
дни недели через числа, но у такого
представления не будет правильной
интерпретации. С какого дня начинается
неделя — с понедельника или воскресенья?
Неделя начинается с нуля или единицы?
Ответы на данные вопросы представляют
собой произвольные решения, которые
влияют на результат. Можно позволить
программисту сделать свой выбор, однако
полученная в результате неструктурированная
среда легко приведёт к ошибкам.
не
является числом. Можно представлять
дни недели через числа, но у такого
представления не будет правильной
интерпретации. С какого дня начинается
неделя — с понедельника или воскресенья?
Неделя начинается с нуля или единицы?
Ответы на данные вопросы представляют
собой произвольные решения, которые
влияют на результат. Можно позволить
программисту сделать свой выбор, однако
полученная в результате неструктурированная
среда легко приведёт к ошибкам.
Приемлемым способом является трактовка
данных так, что у них есть некий тип:
целые числа, числа с плавающей точкой,
символьные строки и т. д. Таким образом,
как только определяется переменная в
программе, необходимо сделать и
«декларацию типа», которая описывает
тип этой переменной. Например, можно
записать: ![]() .
Подобный способ записи используется в
таких языках программирования, как Ada,
Pascal и некоторых других. Также широко
распространены и другие способы записи,
в связи с чем система должна иметь
«валидатор типов» (обычно являющийся
частью компилятора), который не позволяет
применять программу к данным неверного
типа.
.
Подобный способ записи используется в
таких языках программирования, как Ada,
Pascal и некоторых других. Также широко
распространены и другие способы записи,
в связи с чем система должна иметь
«валидатор типов» (обычно являющийся
частью компилятора), который не позволяет
применять программу к данным неверного
типа.
В математике данная идея находит
выражение в более продвинутой
версии
![]() -исчисления
— типизированном
-исчисления
— типизированном ![]() -исчислении,
где каждый терм имеет тип, и является
основной для теории категорий, в которой
каждый морфизм напоминает чёрный ящик
с входным и выходным потоком определённого
типа:
-исчислении,
где каждый терм имеет тип, и является
основной для теории категорий, в которой
каждый морфизм напоминает чёрный ящик
с входным и выходным потоком определённого
типа:
![]()
Если тип выхода первого ящика не совпадает с типом входа второго, соединять их бессмысленно:
![]()
Действительно, существует тесная
связь между типизированным
![]() -исчислением
и декартовыми замкнутыми категориями.
Она была открыта Дж. Ламбеком в 1980 году
[66]. Грубо говоря, теория
типизированного
-исчислением
и декартовыми замкнутыми категориями.
Она была открыта Дж. Ламбеком в 1980 году
[66]. Грубо говоря, теория
типизированного ![]() -исчисления
представляет собой очень простой
функциональный язык программирования
c точно определённым набором базовых
типов данных, на основе которых могут
быть построены более сложные типы
данных, а также с определённым набором
базовых термов, на основании которых
могут быть построены более сложные
термы. Типы данных этого языка
являются объектами в декартовой
замкнутой категории, в то время как
программы, то есть термы, представляют
собой морфизмы.
-исчисления
представляет собой очень простой
функциональный язык программирования
c точно определённым набором базовых
типов данных, на основе которых могут
быть построены более сложные типы
данных, а также с определённым набором
базовых термов, на основании которых
могут быть построены более сложные
термы. Типы данных этого языка
являются объектами в декартовой
замкнутой категории, в то время как
программы, то есть термы, представляют
собой морфизмы.
Тут авторы допускают небольшую
небрежность. Из подраздела 3.3 ясно, что
в логике можно построить замкнутые
моноидальные категории, где морфизмами
являются классы эквивалентности
доказательств. Необходимо, чтобы эти
классы эквивалентности подчинялись
аксиомам замкнутой моноидальной
категории. Таким же образом, если получать
замкнутые моноидальные категории из
информатики, то необходимо, чтобы
морфизмами были классы эквивалентности
термов. Два терма считаются эквивалентными,
если один можно получить из другого при
помощи правил подстановки: ![]() -редукции,
-редукции, ![]() -редукции
и
-редукции
и ![]() -конверсии.
Как было показано, данные правила
подстановки представляют собой процесс
выполнения программы. Например, в
бестиповом
лямбда-исчислении термы
-конверсии.
Как было показано, данные правила
подстановки представляют собой процесс
выполнения программы. Например, в
бестиповом
лямбда-исчислении термы
![]() и
и ![]() различаются
только применением правил подстановки,
поэтому они соответствуют одному и тому
же морфизму. Таким образом, если
производится построение декартовой
замкнутой категории на основе
типизированного
различаются
только применением правил подстановки,
поэтому они соответствуют одному и тому
же морфизму. Таким образом, если
производится построение декартовой
замкнутой категории на основе
типизированного ![]() -исчисления,
то процесс вычисления игнорируется.
Для того чтобы этого избежать, необходимо
работать с декартовой замкнутой
2-категорией, которая имеет:
-исчисления,
то процесс вычисления игнорируется.
Для того чтобы этого избежать, необходимо
работать с декартовой замкнутой
2-категорией, которая имеет:
-
типы в качестве объектов;
-
термы в качестве морфизмов;
-
классы эквивалентности по правилам подстановки в качестве 2-морфизмов.
Подробно данная категория описана в
работах Р. А. Дж. Сили [84],
Б. Хилькена
[50] и П. Мелье [73]. Когда-нибудь вышеупомянутые
работы станут частью большого
![]() -категориального
Розеттского камня, как было упомянуто
в подразделе 2.5.
-категориального
Розеттского камня, как было упомянуто
в подразделе 2.5.
В любом случае, Дж. Ламбек показал, что
любое типизированное
![]() -исчисление
даёт декартову замкнутую категорию, и
наоборот, любая декартова замкнутая
категория соответствует типизированному
-исчисление
даёт декартову замкнутую категорию, и
наоборот, любая декартова замкнутая
категория соответствует типизированному
![]() -исчислению.
Данное открытие предполагает широкое
поле деятельности на стыке теории
категорий и компьютерных наук. Нет
возможности кратко охарактеризовать
количество необходимой работы в данном
направлении, хотя это составляет ключевой
аспект нового Розеттского камня. Для
начала стоит обратить внимание на книгу
Р. Л. Кроула [34] и обзорную статью П. Дж.
Скотта [80], которую можно просмотреть в
он-лайн режиме.
-исчислению.
Данное открытие предполагает широкое
поле деятельности на стыке теории
категорий и компьютерных наук. Нет
возможности кратко охарактеризовать
количество необходимой работы в данном
направлении, хотя это составляет ключевой
аспект нового Розеттского камня. Для
начала стоит обратить внимание на книгу
Р. Л. Кроула [34] и обзорную статью П. Дж.
Скотта [80], которую можно просмотреть в
он-лайн режиме.
Цель авторов более узка. Во-первых, в подразделе 4.2 будет показано, как каждое
«![]() -исчисление»
строит декартову замкнутую категорию
и наоборот. Изложение ведётся по работе
Дж. Ламбека и П. Дж. Скотта [67] в несколько
упрощённом виде. Далее в подразделе 4.3
описывается то, как произвольная
«линейная теория типов» даёт замкнутую
симметричную моноидальную категорию
и наоборот.
-исчисление»
строит декартову замкнутую категорию
и наоборот. Изложение ведётся по работе
Дж. Ламбека и П. Дж. Скотта [67] в несколько
упрощённом виде. Далее в подразделе 4.3
описывается то, как произвольная
«линейная теория типов» даёт замкнутую
симметричную моноидальную категорию
и наоборот.
Основной идея заключается в том, что
«линейная теория типов» представляет
собой язык программирования, который
подходит и для классических, и для
квантовых вычислений. Данный язык
отличается от типизированного ![]() -исчисления
тем, что он запрещает дублирование и
удаление данных, исключая случаи явного
указания. Причина отличия в том, что
каждый объект в декартовой категории
связан с морфизмами «дублирования» и
«удаления»:
-исчисления
тем, что он запрещает дублирование и
удаление данных, исключая случаи явного
указания. Причина отличия в том, что
каждый объект в декартовой категории
связан с морфизмами «дублирования» и
«удаления»:
![]() и
и ![]() ,
в то время как в симметричной моноидальной
категории обычно подобные морфизмы
отсутствуют. Как видно из подраздела
2.3, удачным примером такой категории
является категория
,
в то время как в симметричной моноидальной
категории обычно подобные морфизмы
отсутствуют. Как видно из подраздела
2.3, удачным примером такой категории
является категория ![]() с
её обычным тензорным произведением.
Так, язык программирования, подходящий
для квантовых вычислений, не должен
иметь возможности дублировать произвольные
типы данных [28, 100].
с
её обычным тензорным произведением.
Так, язык программирования, подходящий
для квантовых вычислений, не должен
иметь возможности дублировать произвольные
типы данных [28, 100].
Различные версии «квантового» или
«линейного» ![]() -исчисления
уже изучались, например, Н. Бентоном,
Дж. Бирманом, В. де Пайвой и М. Хайландом
[21], М. Доркой и А. Ван Тондером [98], П.
Сэлинджером и Б. Валироном [88], а С.
Абрамский и Н. Тзевелекос написали
статью по этому вопросу [6]. Авторы же
рассматривают «линейные теории типов»,
разработанные Саймоно Амблером в его
диссертации в 1991 году [7].
4.2.
Типизированное
-исчисления
уже изучались, например, Н. Бентоном,
Дж. Бирманом, В. де Пайвой и М. Хайландом
[21], М. Доркой и А. Ван Тондером [98], П.
Сэлинджером и Б. Валироном [88], а С.
Абрамский и Н. Тзевелекос написали
статью по этому вопросу [6]. Авторы же
рассматривают «линейные теории типов»,
разработанные Саймоно Амблером в его
диссертации в 1991 году [7].
4.2.
Типизированное ![]() -исчисление
Как
и в бестиповом
-исчисление
Как
и в бестиповом ![]() -исчислении,
которое описано в предыдущем подразделе,
типизированное
-исчислении,
которое описано в предыдущем подразделе,
типизированное ![]() -исчисление
использует термы для представления и
данных, и программ. Однако в этом случае
каждый терм имеет определённый тип.
Полагается, что программа, которая
получает на вход данные типа
-исчисление
использует термы для представления и
данных, и программ. Однако в этом случае
каждый терм имеет определённый тип.
Полагается, что программа, которая
получает на вход данные типа ![]() и
возвращает результат типа
и
возвращает результат типа ![]() ,
имеет тип
,
имеет тип ![]() .
Таким образом, можно применять терм
.
Таким образом, можно применять терм ![]() к
терму
к
терму ![]() типа
типа ![]() только в случае, если терм
только в случае, если терм ![]() имеет
тип
имеет
тип ![]() ,
а в результате применения будет получен
строго определённый терм
,
а в результате применения будет получен
строго определённый терм ![]() типа
типа ![]() .
При этом
.
При этом
![]() обозначается
как функциональный тип.
обозначается
как функциональный тип.
Когда бы ни вводилась переменная,
необходимо определить её тип. К примеру,
можно записать
![]() ,
что обозначает: терм
,
что обозначает: терм ![]() имеет
тип
имеет
тип ![]() .
Так что в
.
Так что в ![]() -абстракциях
вместо выражений наподобие
-абстракциях
вместо выражений наподобие
![]() ,
записываются выражения вида
,
записываются выражения вида ![]() ,
где переменная
,
где переменная ![]() имеет
тип
имеет
тип ![]() .
Например, вот простая программа, которая
принимает на вход программу типа
.
Например, вот простая программа, которая
принимает на вход программу типа ![]() и
дублирует её применение:
и
дублирует её применение: ![]() .
.
В оригинальном ![]() -исчислении
все программы принимают на вход одиночные
порции данных. Другими словами, они
выполняют унарные функции. Это не
является ограничением, поскольку
многоаргументные функции можно определять
при помощи приёма, названного
«каррированием» и описанного в подразделе
2.6. Данная техника превращает
многоаргументную функцию в унарную
функцию, получающую на вход первый
аргумент и возвращающую в качестве
результата функцию от оставшихся
аргументов. Пример был показан в
предыдущем подразделе: программа
-исчислении
все программы принимают на вход одиночные
порции данных. Другими словами, они
выполняют унарные функции. Это не
является ограничением, поскольку
многоаргументные функции можно определять
при помощи приёма, названного
«каррированием» и описанного в подразделе
2.6. Данная техника превращает
многоаргументную функцию в унарную
функцию, получающую на вход первый
аргумент и возвращающую в качестве
результата функцию от оставшихся
аргументов. Пример был показан в
предыдущем подразделе: программа ![]() .То
есть, если терм
.То
есть, если терм ![]() производит
умножение на
производит
умножение на ![]() ,
то
,
то ![]() .
.
Хотя трактовка всех программ в виде
унарных функций весьма удобна, она не
особо устроит программистов. Так что в
типизированном
![]() -исчислении
также вводятся произведения: для заданных
типов
-исчислении
также вводятся произведения: для заданных
типов ![]() и
и ![]() существует
тип
существует
тип ![]() ,
называемый произведением типов.
Можно представить данные типа
,
называемый произведением типов.
Можно представить данные типа ![]() как
упорядоченные пары, которые содержат
данные типов
как
упорядоченные пары, которые содержат
данные типов ![]() и
и ![]() на
первом и втором местах соответственно.
К примеру, для заданных термов
на
первом и втором местах соответственно.
К примеру, для заданных термов ![]() и
и ![]() существует
терм
существует
терм ![]() .
Также для заданного терма
.
Также для заданного терма
![]() существуют
термы
существуют
термы ![]() и
и ![]() ,
которые возвращают первый и второй
компонент пары
,
которые возвращают первый и второй
компонент пары ![]() соответственно.
Помимо того, есть правила подстановки,
утверждающие:
соответственно.
Помимо того, есть правила подстановки,
утверждающие:
Произведения типов позволяют писать
программы, принимающие на вход более
одного аргумента. Более того, они
позволяют работать с программами,
которые выдают на выходе более одного
результата. Например, пусть имеется
тип ![]() .
Тогда можно написать программу, которая
получает на вход целое число типа
.
Тогда можно написать программу, которая
получает на вход целое число типа ![]() и
дублирует его:
и
дублирует его: ![]() .
Сама программа проста:
.
Сама программа проста:
![]() .
Но её будет невозможно написать в случае,
если дублирование информации запрещено,
однако в настоящем подразделе авторы
оперируют классическими декартовыми
замкнутыми категориями.
.
Но её будет невозможно написать в случае,
если дублирование информации запрещено,
однако в настоящем подразделе авторы
оперируют классическими декартовыми
замкнутыми категориями.
В типизированном ![]() -исчислении
также имеется специальный тип, называемый
«единичным типом» и обозначаемый как
-исчислении
также имеется специальный тип, называемый
«единичным типом» и обозначаемый как ![]() .
Имеется единственный терм этого типа,
который обозначается как
.
Имеется единственный терм этого типа,
который обозначается как ![]() .
С точки зрения теории категорий
необходимость такого типа совершенно
ясна: категория с конечными произведениями
должна не только иметь бинарную операцию
произведения, но и финальный объект
(см. определение 10). Например, в категории
.
С точки зрения теории категорий
необходимость такого типа совершенно
ясна: категория с конечными произведениями
должна не только иметь бинарную операцию
произведения, но и финальный объект
(см. определение 10). Например, в категории
![]() финальным
объектом может быть произвольный
синглетон (одноэлементное множество),
а элемент
финальным
объектом может быть произвольный
синглетон (одноэлементное множество),
а элемент ![]() представляет
собой единственный элемент такого
множества. Может быть не совсем ясно,
зачем этот тип необходим в программировании.
Одной из причин является то, что он
позволяет рассматривать константы
типа
представляет
собой единственный элемент такого
множества. Может быть не совсем ясно,
зачем этот тип необходим в программировании.
Одной из причин является то, что он
позволяет рассматривать константы
типа ![]() в
качестве функций типа
в
качестве функций типа ![]() ,
то есть нуль-арных функций, которые не
принимают на вход никаких аргументов.
Есть и некоторые другие причины, но речь
сейчас пойдет не о них. Достаточно
сказать, что такие языки программирования,
как Haskell и Lisp, а также такие широко
распространённые языки, как C, C++ и Java,
имеют единичный тип.
,
то есть нуль-арных функций, которые не
принимают на вход никаких аргументов.
Есть и некоторые другие причины, но речь
сейчас пойдет не о них. Достаточно
сказать, что такие языки программирования,
как Haskell и Lisp, а также такие широко
распространённые языки, как C, C++ и Java,
имеют единичный тип.
После введения основных компонентов
типизированного ![]() -исчисления,
необходимо провести некоторые более
существенные обоснования. Как будет
показано, типизированное
-исчисления,
необходимо провести некоторые более
существенные обоснования. Как будет
показано, типизированное ![]() -исчисление
состоит из типов, термов и правил
подстановки. На основе
типизированного
-исчисление
состоит из типов, термов и правил
подстановки. На основе
типизированного ![]() -исчисления
можно получить декартову замкнутую
категорию. Типы соответствуют объектам,
термы — морфизмам, а правила подстановки
соответствуют отношениям между
морфизмами.
-исчисления
можно получить декартову замкнутую
категорию. Типы соответствуют объектам,
термы — морфизмам, а правила подстановки
соответствуют отношениям между
морфизмами.
Во-первых, типы индуктивно определяются следующим образом:
-
Базовые типы: произвольно выбранное множество типов;
-
Произведения типов: для заданных типов
 и
и 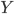 имеется
тип
имеется
тип  ;
; -
Функциональные типы: для заданных типов
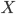 и
и 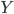 имеется
тип
имеется
тип  ;
; -
Единичный тип: имеется специальный тип
 .
.
Возможны неожиданные отношения между
типами. Например, может существовать
тип ![]() такой,
что
такой,
что ![]() .
При этом на систему типов накладываются
следующие ограничения:
.
При этом на систему типов накладываются
следующие ограничения:
-
Если
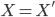 и
и 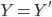 ,
то
,
то 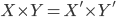 .
. -
Если
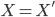 и
и 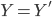 ,
то
,
то 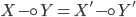 .
.
Теперь необходимо определить, что
такое терм. Каждый терм имеет
определённый тип, и если терм ![]() имеет
тип
имеет
тип ![]() ,
то это записывается как
,
то это записывается как ![]() .
Правила построения термов следующие:
.
Правила построения термов следующие:
-
Базовые термы: для каждого типа
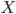 имеется
множество базовых термов данного типа;
имеется
множество базовых термов данного типа; -
Переменные: для каждого типа
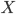 имеется
счётное бесконечное множество термов
этого типа, называемых переменными
типа
имеется
счётное бесконечное множество термов
этого типа, называемых переменными
типа 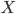 ;
; -
Применение: если
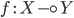 и
и 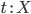 ,
то имеется терм
,
то имеется терм 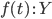 ;
; -
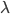 -абстракция:
если имеется переменная
-абстракция:
если имеется переменная 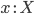 и
терм
и
терм 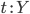 ,
то существует терм
,
то существует терм 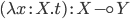 ;
; -
Парообразование: если имеются термы
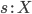 и
и 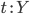 ,
то существует терм
,
то существует терм 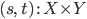 ;
; -
Проекция: если
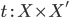 ,
то существуют термы
,
то существуют термы 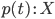 и
и  ;
; -
Единичный терм: существует специальный терм
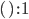 .
.
Наконец, имеются правила подстановки
для преобразования термов одного типа.
Для заданного фиксированного множества
переменных ![]() существуют
правила подстановки термов одного типа,
все свободные переменные которых
принадлежат множеству
существуют
правила подстановки термов одного типа,
все свободные переменные которых
принадлежат множеству ![]() .
В данном случае правила подстановки
необходимы только для понимания того,
когда два терма определяют один и тот
же морфизм в декартовой замкнутой
категории, которая будет построена. Так
что важны не сами по себе правила
подстановки, а то отношение эквивалентности,
которое строится на их основе и
записывается как
.
В данном случае правила подстановки
необходимы только для понимания того,
когда два терма определяют один и тот
же морфизм в декартовой замкнутой
категории, которая будет построена. Так
что важны не сами по себе правила
подстановки, а то отношение эквивалентности,
которое строится на их основе и
записывается как ![]() .
.
Отношение ![]() может
быть произвольным отношением
эквивалентности, которое удовлетворяет
нижеизложенным правилам. В дальнейшем
описании запись
может
быть произвольным отношением
эквивалентности, которое удовлетворяет
нижеизложенным правилам. В дальнейшем
описании запись ![]() обозначает
результат замены всех свободных вхождений
переменной
обозначает
результат замены всех свободных вхождений
переменной ![]() в
терме
в
терме ![]() термом
термом ![]() .
Также под словом «терм» по умолчанию
подразумевается словосочетание «терм,
все свободные переменные которого
входят в множество
.
Также под словом «терм» по умолчанию
подразумевается словосочетание «терм,
все свободные переменные которого
входят в множество ![]() ».
».
-
Сохранение типа: если
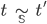 ,
то термы
,
то термы 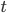 и
и 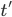 должны
иметь один и тот же тип, все свободные
переменные которого находятся в
множестве
должны
иметь один и тот же тип, все свободные
переменные которого находятся в
множестве 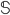 .
. -
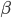 -редукция:
пусть
-редукция:
пусть 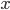 есть
переменная типа
есть
переменная типа 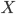 ,
,
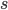 есть
терм типа
есть
терм типа 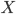 ,
а
,
а  есть
произвольный терм. Если ни одно свободное
вхождение переменной в
есть
произвольный терм. Если ни одно свободное
вхождение переменной в 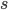 не
становится связанным в
не
становится связанным в 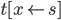 ,
то
,
то 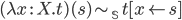 .
. -
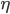 -редукция:
пусть переменная
-редукция:
пусть переменная 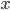 не входит в терм
не входит в терм
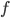 ,
тогда
,
тогда 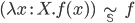 .
. -
 -конверсия:
пусть
-конверсия:
пусть 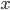 и
и 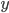 есть
переменные типа
есть
переменные типа  ,
и ни одно свободное вхождение переменной
в терме
,
и ни одно свободное вхождение переменной
в терме 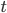 не
становится связанным в
не
становится связанным в 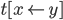 ,
тогда .
,
тогда . -
Применение (аппликация): пусть
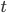 и
и 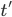 —
термы одного типа
—
термы одного типа 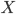 при
истинности
при
истинности 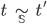 ,
и пусть
,
и пусть 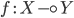 ,
тогда
,
тогда 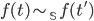 .
. -
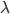 -абстракция:
пусть
-абстракция:
пусть 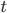 и
и 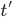 —
термы одного типа
—
термы одного типа 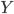 ,
все свободные переменные которых
находятся в множестве
,
все свободные переменные которых
находятся в множестве 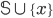 .
Пусть
.
Пусть 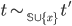 ,
тогда
,
тогда 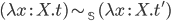 .
. -
Парообразование: если
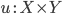 ,
то
,
то 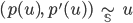 .
. -
Проекции: если
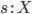 и
и 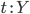 ,
то
,
то 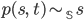 и
и  .
. -
Единичный терм: если
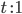 ,
то
,
то 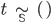 .
.
Теперь можно описать классический
результат Дж. Ламбека по связыванию
типизированных ![]() -исчислений
с декартовыми замкнутыми категориями.
Из типизированного
-исчислений
с декартовыми замкнутыми категориями.
Из типизированного ![]() -исчисления
получается декартова замкнутая
категория
-исчисления
получается декартова замкнутая
категория ![]() ,
для которой:
,
для которой:
-
Объектами являются типы;
-
Морфизмами
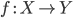 являются
классы эквивалентности пар
являются
классы эквивалентности пар  ,
состоящих из переменных
,
состоящих из переменных 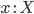 и
термов
и
термов 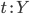 без
свободных переменных, кроме
без
свободных переменных, кроме 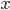 .
Здесь
.
Здесь 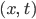 эквивалентно
эквивалентно 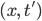 тогда
и только тогда, когда
тогда
и только тогда, когда 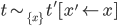 .
. -
Для заданных морфизмов
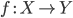 ,
полученного из пары
,
полученного из пары 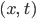 ,
и
,
и 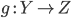 ,
полученного из пары
,
полученного из пары 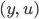 так,
как описано в предыдущем пункте,
композиция
так,
как описано в предыдущем пункте,
композиция 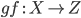 определяется
парой
определяется
парой 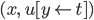 .
.
Данный процесс можно обратить и получить
из декартовой замкнутой категории
типизированное ![]() -исчисление.
Фактически, Дж. Ламбек и П. Дж. Скотт
прекрасно объяснили, как построить
категорию категорий декартовых замкнутых
категорий, а также категорию
типизированных
-исчисление.
Фактически, Дж. Ламбек и П. Дж. Скотт
прекрасно объяснили, как построить
категорию категорий декартовых замкнутых
категорий, а также категорию
типизированных ![]() -исчислений.
Вышеупомянутые учёные построили функторы
для перемещения между категориями, при
этом данные функторы были обратимы с
точностью до естественных преобразований.
Поэтому говорится, что такие категории
«эквивалентны» [67].
4.3.
Теории линейных типов
В своей
диссертации [7] С. Амблер описал, как
применить классический результат Дж.
Ламбека к замкнутым симметричным
моноидальным категориям. Для этого он
заменил типизированное
-исчислений.
Вышеупомянутые учёные построили функторы
для перемещения между категориями, при
этом данные функторы были обратимы с
точностью до естественных преобразований.
Поэтому говорится, что такие категории
«эквивалентны» [67].
4.3.
Теории линейных типов
В своей
диссертации [7] С. Амблер описал, как
применить классический результат Дж.
Ламбека к замкнутым симметричным
моноидальным категориям. Для этого он
заменил типизированное ![]() -исчисление
на «теорию линейных типов». Теория
линейных типов в качестве языка
программирования может использоваться
как для классических, так и для квантовых
вычислений. Как было показано, в
недекартовых категориях, таких как
-исчисление
на «теорию линейных типов». Теория
линейных типов в качестве языка
программирования может использоваться
как для классических, так и для квантовых
вычислений. Как было показано, в
недекартовых категориях, таких как ![]() ,
невозможно свободно дублировать или
удалять информацию. Так что теория
линейных типов не должна разрешать
дублирование или удаление, если
только это явно не указано.
,
невозможно свободно дублировать или
удалять информацию. Так что теория
линейных типов не должна разрешать
дублирование или удаление, если
только это явно не указано.
Чтобы данное правило выполнялось, теория
линейных типов не должна позволять
записывать программы типа ![]() .
Непозволительны даже программы, которые
дублируют применение заданной программы,
вроде следующей:
.
Непозволительны даже программы, которые
дублируют применение заданной программы,
вроде следующей: ![]() ,
поскольку в ней происходит повторное
использование переменной
,
поскольку в ней происходит повторное
использование переменной ![]() .
С другой стороны, программа, которая
осуществляет композицию двух заданных
программ, разрешена.
.
С другой стороны, программа, которая
осуществляет композицию двух заданных
программ, разрешена.
Для соответствия данным ограничениям
теория линейных типов рассматривает
переменные под совершенно иным углом,
нежели типизированное ![]() -исчисление.
Фактически, в теории линейных типов
любой терм может содержать заданную
переменную не более одного раза.
Однако теория линейных типов ещё больше
отличается от типизированного
-исчисление.
Фактически, в теории линейных типов
любой терм может содержать заданную
переменную не более одного раза.
Однако теория линейных типов ещё больше
отличается от типизированного ![]() -исчисления
в другом аспекте. Она не использует
-исчисления
в другом аспекте. Она не использует ![]() -абстракции,
но вместо них использует «комбинаторы».
-абстракции,
но вместо них использует «комбинаторы».
Идея комбинатора очень проста, фактически,
комбинаторы предшествовали ![]() -исчислению.
Комбинаторная логика зародилась в 1924
году в статье М. Шейнфинкеля [83], и заново
основательно исследована Х. Б. Карри
[35] в 1927 году. Можно заметить, что в данных
работах комбинаторная логика очень
напоминает бестиповое
-исчислению.
Комбинаторная логика зародилась в 1924
году в статье М. Шейнфинкеля [83], и заново
основательно исследована Х. Б. Карри
[35] в 1927 году. Можно заметить, что в данных
работах комбинаторная логика очень
напоминает бестиповое
![]() -исчисление,
в котором отсутствуют переменные. При
помощи начальных термов, называемых
«комбинаторами», можно строить новые
термы только при помощи операции
применения: применяя, к примеру, терм
-исчисление,
в котором отсутствуют переменные. При
помощи начальных термов, называемых
«комбинаторами», можно строить новые
термы только при помощи операции
применения: применяя, к примеру, терм ![]() к
терму
к
терму ![]() и
получить терм
и
получить терм ![]() .
.
Для того чтобы построить полный по
Тьюрингу язык программирования на такой
небогатой основе, необходимо иметь
базовый набор комбинаторов. Поразительно
то, что для этих целей достаточно всего
лишь трёх. Фактически, возможно
использование одного верно
подобранного комбинатора, однако данный
способ мало понятен, так что в дальнейшем
будет описан широко используемый набор
из трёх комбинаторов, первый из которых
называется комбинатором ![]() ,
он работает как функция тождества,
поскольку для него используется следующее
правило подстановки:
,
он работает как функция тождества,
поскольку для него используется следующее
правило подстановки:
![]() для
произвольного терма
для
произвольного терма ![]() .
Второй комбинатор
.
Второй комбинатор ![]() возвращает
константную функцию
возвращает
константную функцию ![]() для
произвольного терма
для
произвольного терма ![]() .
Другими словами, для него действует
правило подстановки
.
Другими словами, для него действует
правило подстановки ![]() для
произвольного терма
для
произвольного терма ![]() .
Третий комбинатор
.
Третий комбинатор ![]() представляет
больший интерес. Он получает на вход
три терма и применяет первый терм к
третьему, а затем полученный результат
применяет к результату применения
второго терма к третьему:
представляет
больший интерес. Он получает на вход
три терма и применяет первый терм к
третьему, а затем полученный результат
применяет к результату применения
второго терма к третьему: ![]() .
.
Данные комбинаторы могут быть выражены
через термины бестипового
![]() -исчисления
следующим образом:
-исчисления
следующим образом:
Правила подстановки для этих комбинаторов,
таким образом, следуют из правил
подстановки ![]() -исчисления.
Более того, любая функция, вычисляемая
при помощи
-исчисления.
Более того, любая функция, вычисляемая
при помощи ![]() -исчисления,
может быть вычислена только при помощи
комбинаторов
-исчисления,
может быть вычислена только при помощи
комбинаторов ![]() ,
, ![]() и
и ![]() .
Хотя данное утверждение не способствует
пониманию теории линейных типов,
доказательство всё же будет приведено,
поскольку представляет собой классическое
использование комбинаторов без явного
использования
.
Хотя данное утверждение не способствует
пониманию теории линейных типов,
доказательство всё же будет приведено,
поскольку представляет собой классическое
использование комбинаторов без явного
использования ![]() -абстракций.
-абстракций.
Необходимо отметить, что все переменные
в ![]() -формулах
для трёх комбинаторов
-формулах
для трёх комбинаторов ![]() ,
, ![]() и
и ![]() являются связанными. В более широком
понимании можно говорить о том, что в
являются связанными. В более широком
понимании можно говорить о том, что в
![]() -исчислении комбинатор определяется
как терм, в котором все переменные
связаны. Два комбинатора
-исчислении комбинатор определяется
как терм, в котором все переменные
связаны. Два комбинатора ![]() и
и ![]() считаются экстенсионально
эквивалентными, если они дают одинаковый
результат при применении к любым входным
термам: другими словами, для произвольного
терма
считаются экстенсионально
эквивалентными, если они дают одинаковый
результат при применении к любым входным
термам: другими словами, для произвольного
терма ![]() результаты
применения
результаты
применения ![]() и
и ![]() одинаковы. Существует процесс, называемый
«удалением абстракции», который
преобразует любой комбинатор в
нотации
одинаковы. Существует процесс, называемый
«удалением абстракции», который
преобразует любой комбинатор в
нотации ![]() -исчисления
в экстенсионально эквивалентный,
выраженный только при помощи
комбинаторов
-исчисления
в экстенсионально эквивалентный,
выраженный только при помощи
комбинаторов ![]() ,
, ![]() и
и ![]() .
.
Удаление абстракции работает при
получении на вход терма ![]() с
одиночной
с
одиночной ![]() -абстракцией
и перезаписи его в форме
-абстракцией
и перезаписи его в форме ![]() ,
где терм
,
где терм ![]() не
содержит
не
содержит ![]() -абстракций.
Далее можно применить
-абстракций.
Далее можно применить
![]() -редукцию,
которая утверждает, что
-редукцию,
которая утверждает, что ![]() ,
что позволяет записать терм
,
что позволяет записать терм ![]() в
виде терма
в
виде терма ![]() ,
при этом последний не содержит
никаких
,
при этом последний не содержит
никаких ![]() -абстракций.
Далее запись
-абстракций.
Далее запись ![]() будет
обозначать «произвольный терм
будет
обозначать «произвольный терм ![]() такой,
что
такой,
что ![]() ».
».
Имеется три случая, каждый из которых соответствует определению одного из базовых комбинаторов:
-
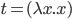 .
Можно перезаписать как
.
Можно перезаписать как 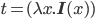 ,
так что
,
так что 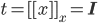 .
. -
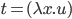 ,
при этом
,
при этом 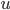 не
зависит от
не
зависит от 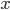 .
Можно перезаписать как
.
Можно перезаписать как 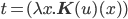 ,
так что
,
так что 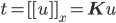 .
. -
 ,
где
,
где 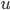 и
и 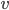 могут
зависеть от
могут
зависеть от 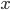 .
Можно перезаписать как
.
Можно перезаписать как 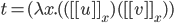 или
или 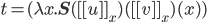 ,
так что
,
так что 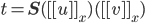 .
.
Теперь возможно удаление любого
количества
![]() -абстракций,
применяя данные правила «изнутри вовне
» (от терма с наибольшим уровнем
вложенности к терму с наименьшим уровнем
вложенности). Для лучшего понимания
рассмотрим терм
-абстракций,
применяя данные правила «изнутри вовне
» (от терма с наибольшим уровнем
вложенности к терму с наименьшим уровнем
вложенности). Для лучшего понимания
рассмотрим терм ![]() ,
который принимает на вход два терма и
возвращает второй. При помощи ранее
описанных правил:
,
который принимает на вход два терма и
возвращает второй. При помощи ранее
описанных правил:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
можно проверить правильность
выполнения:
![]() .
.
Теперь вернёмся к теории линейных типов.
Из описанных ранее комбинаторов только
комбинатор ![]() подходит
для использования в произвольной
замкнутой симметричной моноидальной
категории. Причиной является то, что
комбинатор
подходит
для использования в произвольной
замкнутой симметричной моноидальной
категории. Причиной является то, что
комбинатор ![]() удаляет
данные, в то время как комбинатор
удаляет
данные, в то время как комбинатор ![]() дублирует
их, что видно напрямую из правил
подстановки, которым они удовлетворяют:
дублирует
их, что видно напрямую из правил
подстановки, которым они удовлетворяют:
![]() ,
, ![]() .
.
Каждая теория линейных типов имеет
набор «базовых комбинаторов», которые
ни удаляют, ни дублируют данные. Поскольку
теории линейных типов
обобщают типизированное ![]() -исчисление,
эти базовые комбинаторы имеют типы. С.
Амблер записывал их, оперируя понятиями,
напоминающими понятия морфизмов в
теории категорий.
-исчисление,
эти базовые комбинаторы имеют типы. С.
Амблер записывал их, оперируя понятиями,
напоминающими понятия морфизмов в
теории категорий.
Например, для заданных типов ![]() и
и ![]() в
теории линейных типов существует тип
тензорного произведения
в
теории линейных типов существует тип
тензорного произведения ![]() .
Он аналогичен типу произведения в
типизированном
.
Он аналогичен типу произведения в
типизированном ![]() -исчислении.
В частности, заданные термы
-исчислении.
В частности, заданные термы
![]() и
и ![]() можно
комбинировать для получения терма
типа
можно
комбинировать для получения терма
типа ![]() ,
который обозначается как
,
который обозначается как ![]() .
Удаление скобок в повторяющемся тензорном
произведении производится при помощи
базового комбинатора:
.
Удаление скобок в повторяющемся тензорном
произведении производится при помощи
базового комбинатора: ![]() .
Этот комбинатор имеет следующее правило
подстановки:
.
Этот комбинатор имеет следующее правило
подстановки: ![]() для
произвольных термов
для
произвольных термов ![]() ,
, ![]() и
и ![]() .
.
Конечно, базовый комбинатор ![]() —
это просто другая форма записи уже
известного по теории категорий
ассоциатора. Несомненно, все базовые
комбинаторы получаются на основе
естественных и диестественных
преобразований, скрыто участвующих
в определении «замкнутой симметричной
моноидальной категории». В дополнение
к ним в любой заданной теории линейных
типов также имеются комбинаторы,
называемые «функциональными символами».
Они строятся на основе морфизмов,
свойственных заданной категории.
Например, пусть в некоторой категории
тензорное произведение
—
это просто другая форма записи уже
известного по теории категорий
ассоциатора. Несомненно, все базовые
комбинаторы получаются на основе
естественных и диестественных
преобразований, скрыто участвующих
в определении «замкнутой симметричной
моноидальной категории». В дополнение
к ним в любой заданной теории линейных
типов также имеются комбинаторы,
называемые «функциональными символами».
Они строятся на основе морфизмов,
свойственных заданной категории.
Например, пусть в некоторой категории
тензорное произведение ![]() является
декартовым произведением. В этом случае
соответствующая теория линейных типов
должна будет иметь следующий функциональный
символ:
является
декартовым произведением. В этом случае
соответствующая теория линейных типов
должна будет иметь следующий функциональный
символ: ![]() ,
который позволяет дублировать данные
типа
,
который позволяет дублировать данные
типа ![]() ,
а также функциональные символы
,
а также функциональные символы ![]() и
и ![]() ,
проецирующие декартово произведение
на первый или второй множитель. Для
символов необходимо использовать
правила подстановки:
,
проецирующие декартово произведение
на первый или второй множитель. Для
символов необходимо использовать
правила подстановки:
Так что, поскольку дублирование и удаление данных не являются «встроенными возможностями» операций в теорию линейных типов, их можно добавлять по желанию.
При помощи комбинаторов можно попытаться
создать язык программирования, который
бы использовался для замкнутых
симметричных моноидальных категорий
и не содержал бы переменных. С. Амблер
пошёл по иному пути. Он оставил в своей
системе переменные, но они играют в ней
совершенно иную роль, нежели в
![]() -исчислении,
гораздо более простую. Она
заключается в том, чтобы помочь определить
эквивалентные термы. Более того,
абстракции не играют никакой роли в
теории линейных типов, так что не
возникает кардинальных различий между
связанными и свободными переменными!
Собственно, все переменные являются
свободными. Более того, любой терм
содержит заданную переменную не более
одного раза.
-исчислении,
гораздо более простую. Она
заключается в том, чтобы помочь определить
эквивалентные термы. Более того,
абстракции не играют никакой роли в
теории линейных типов, так что не
возникает кардинальных различий между
связанными и свободными переменными!
Собственно, все переменные являются
свободными. Более того, любой терм
содержит заданную переменную не более
одного раза.
Теперь можно перейти к более обстоятельному описанию теории линейных типов. Теория линейных типов состоит из типов, комбинаторов, термов и правил подстановки. Типы соответствуют объектам в замкнутой симметричной моноидальной категории, в то время как классы эквивалентности комбинаторов соответствуют в ней морфизмам. Термы и правила подстановки используются только для определения отношения эквивалентности.
Во-первых, множество типов определяется индуктивно следующим образом:
-
Базовые типы: имеется произвольно выбранное множество типов, называемых базовыми.
-
Типы-произведения: для заданных типов
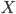 и
и 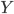 имеется
тип
имеется
тип
![]() .
.
-
Функциональные типы: для заданных типов
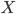 и
и 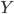 имеется
тип
имеется
тип 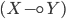 .
. -
Тривиальный тип: имеется тип
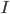 .
.
Между типами могут быть отношения, однако требуется:
-
Если
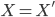 и
и 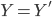 ,
то
,
то 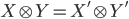 .
. -
Если
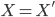 и
и 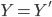 ,
то
,
то 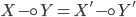 .
.
Во-вторых, для каждой пары типов ![]() и
и ![]() имеется
набор комбинаторов формы
имеется
набор комбинаторов формы ![]() .
Комбинаторы определяются при помощи
следующих индуктивных правил:
.
Комбинаторы определяются при помощи
следующих индуктивных правил:
-
Для заданных типов
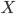 и
и 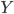 имеется
произвольно выбранное множество
комбинаторов
имеется
произвольно выбранное множество
комбинаторов  ,
называемых функциональными
символами.
,
называемых функциональными
символами. -
Для заданных типов
 ,
,  и
и  имеется
следующий набор комбинаторов,
называемых базовыми комбинаторами:
имеется
следующий набор комбинаторов,
называемых базовыми комбинаторами: -
-
Если
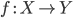 и
и 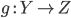 —
комбинаторы, то
—
комбинаторы, то 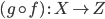 также
комбинатор.
также
комбинатор. -
Если
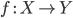 и
и 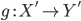 —
комбинаторы, то
—
комбинаторы, то 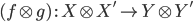 также
комбинатор.
также
комбинатор. -
Если
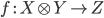 —
комбинатор, то его можно каррировать,
получив комбинатор
—
комбинатор, то его можно каррировать,
получив комбинатор  .
.
Если опустить индексы у базовых
комбинаторов, то недоразумений обычно
не возникает. Например, можно записывать
просто ![]() вместо
вместо ![]() .
.
В-третьих, в теории линейных типов
имеются термы заданного типа.
Как обычно, запись ![]() обозначает
то, что терм
обозначает
то, что терм ![]() имеет
тип
имеет
тип ![]() .
Термы определяются индуктивно следующим
образом:
.
Термы определяются индуктивно следующим
образом:
-
Для каждого типа
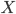 имеется
счётное бесконечное множество переменных этого
типа. Если
имеется
счётное бесконечное множество переменных этого
типа. Если 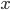 является
переменной типа
является
переменной типа 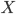 ,
то
,
то 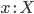 .
. -
Имеется терм
 такой,
что
такой,
что 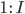 .
. -
Если
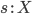 и
и 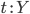 ,
то существует терм
,
то существует терм 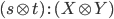 ,
если только одна и та же переменная не
содержится одновременно в обоих
термах
,
если только одна и та же переменная не
содержится одновременно в обоих
термах 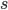 и
и 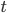 .
. -
Если
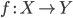 является
комбинатором, и
является
комбинатором, и 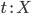 ,
то существует терм
,
то существует терм 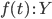 .
.
Необходимо отметить, что любая заданная переменная может находиться в любом терме не более одного раза.
И в-четвёртых, теория линейных типов
содержит правила подстановки,
которые применяются к термам одного
типа. Как и в случае с типизированным
![]() -исчислением,
здесь будет приниматься во внимание
только отношение эквивалентности
-исчислением,
здесь будет приниматься во внимание
только отношение эквивалентности ![]() ,
генерируемое данными правилами
подстановки. Это отношение эквивалетности
должно иметь все свойства, перечисленные
ниже. Далее говорится о том, что терм
является базовым, если он не
содержит в своей записи комбинаторов.
Таким термом является повторяющееся
тензорное произведение различных
переменных, как, например:
,
генерируемое данными правилами
подстановки. Это отношение эквивалетности
должно иметь все свойства, перечисленные
ниже. Далее говорится о том, что терм
является базовым, если он не
содержит в своей записи комбинаторов.
Таким термом является повторяющееся
тензорное произведение различных
переменных, как, например: ![]() .
.
А вот свойства, которые должно иметь
отношение эквивалентности ![]() :
:
-
Если
 ,
то термы
,
то термы 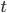 и
и 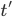 должны
быть одного типа и содержать одни и те
же переменные.
должны
быть одного типа и содержать одни и те
же переменные. -
Отношение эквивалентности является подстановочным, что значит:
-
Для заданных термов
 и
переменной
и
переменной 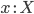 ,
а также термов
,
а также термов 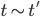 типа
типа  ,
переменные которых не встречаются ни
в терме
,
переменные которых не встречаются ни
в терме 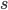 ,
ни в терме
,
ни в терме 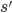 ,
выполняется
,
выполняется 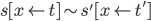 .
. -
Для заданного базового терма
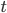 такого
же типа, что и переменная
такого
же типа, что и переменная 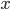 ,
если ни одна из переменных терма
,
если ни одна из переменных терма 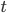 не
встречается в термах
не
встречается в термах 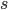 и
и 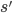 ,
если
,
если 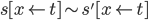 ,
то
,
то  .
.
-
-
Отношение эквивалентности экстенсионально: если для
 и
и  имеет
место
имеет
место 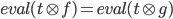 для
всех базовых термов
для
всех базовых термов 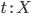 ,
то
,
то 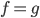 .
. -
Имеет место:
-
Необходимо отметить, что в термах
могут быть переменные, проявляющиеся
в любом месте в записи терма. Например,
если ![]() ,
, ![]() и
и ![]() переменные
типов
переменные
типов ![]() ,
, ![]() и
и ![]() соответственно,
и
соответственно,
и ![]() является
функциональным символом, то
выражение
является
функциональным символом, то
выражение ![]() является
термом типа
является
термом типа ![]() .
Однако при этом каждый терм
.
Однако при этом каждый терм ![]() эквивалентен
некоторому терму в форме
эквивалентен
некоторому терму в форме ![]() ,
где
,
где ![]() — комбинаторная часть терма
— комбинаторная часть терма ![]() ,
а
,
а ![]() — базовый терм, называемый переменной
частью терма
— базовый терм, называемый переменной
частью терма ![]() .
Например, терм в предыдущем примере
эквивалентен терму
.
Например, терм в предыдущем примере
эквивалентен терму ![]() .
Комбинаторная и переменная часть могут
быть индуктивно получены следующим
образом:
.
Комбинаторная и переменная часть могут
быть индуктивно получены следующим
образом:
-
Для
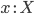 имеет
место
имеет
место 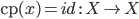 .
. -
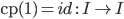 .
. -
Для произвольных термов
 и
и  имеет
место
имеет
место 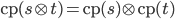 .
. -
Для произвольного терма
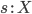 и
комбинатора
и
комбинатора 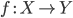 имеет
место
имеет
место 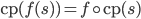 .
.
-
Для
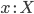 имеет
место
имеет
место 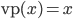 .
. -
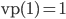 .
. -
Для произвольных термов
 и
и 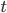 имеет
место
имеет
место 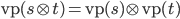 .
. -
Для произвольного терма
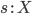 и
комбинатора
и
комбинатора 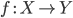 имеет
место
имеет
место 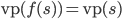 .
.
Теперь необходимо рассмотреть теорию
линейных типов. Первым основным выводом
С. Амблера является то, что существует
симметричная моноидальная категория,
объектами которой являются типы, а
морфизмами — классы эквивалентности
комбинаторов. Отношение эквивалентности
между комбинаторами определяется
следующим образом: два комбинатора ![]() эквивалентны
тогда и только тогда, когда
эквивалентны
тогда и только тогда, когда ![]() для
некоторого базового терма
для
некоторого базового терма ![]() .
Фактически С. Амблер показал, что
.
Фактически С. Амблер показал, что ![]() для
некоторого базового терма
для
некоторого базового терма ![]() тогда
и только тогда, когда
тогда
и только тогда, когда ![]() для всех базовых
термов.
для всех базовых
термов.
Ещё одни итогом работы С. Амблера стала
техника построения теории линейных
типов на основе замкнутой симметричной
моноидальной категории ![]() .
Пусть в категории
.
Пусть в категории ![]() имеются
композиция
имеются
композиция ![]() ,
тензорное произведение
,
тензорное произведение ![]() ,
внутренний
,
внутренний ![]() -функтор
-функтор ![]() и
единичный объект
и
единичный объект ![]() .
Пусть базовые типы теории линейных
типов будут объектами категории
.
Пусть базовые типы теории линейных
типов будут объектами категории ![]() .
В качестве уравнений соответствия
используются следующие:
.
В качестве уравнений соответствия
используются следующие:
Функциональные символы являются
морфизмами категории ![]() .
В качестве отношения эквивалентности
между термами необходимо взять минимально
допустимое отношение эквивалентности,
которое удовлетворяет следующим
ограничениям:
.
В качестве отношения эквивалентности
между термами необходимо взять минимально
допустимое отношение эквивалентности,
которое удовлетворяет следующим
ограничениям:
В этом случае можно определить:
и всё!
С. Амблер также показал, что данная процедура является «обратной» к процедуре получения замкнутой симметричной моноидальной категории в теорию линейных типов. Выражаясь яснее, он описал категорию замкнутых симметричных моноидальных категорий (которая хорошо известна), а также категорию теорий линейных типов. С. Амблер построил функторы между вышеупомянутыми категориями (в обе стороны), которые основаны на процедурах, кратко описанных ранее, и показал, что данные функторы являются обращениями друг друга с точностью до естественного изоморфизма. Так что данные категории являются «эквивалентными».
В данном разделе былы описаны замкнутые
симметричные моноидальные категории.
Что же касается замкнутых категорий,
которые являются просто сплетёнными
или только моноидальными, то предполагается
(хотя не проверено), что языки
программирования, подходящие для данных
видов категорий, могут быть получены
из системы С. Амблера при устранении
некоторых возможностей. Для получения
языка для сплетённой моноидальной
категории очевидным изменением будет
удаление правила подстановки для
комбинатора ![]() ,
а также добавление двух правил подстановки,
соответствующих шестиугольным уравнениям
(см. подраздел 2.4). При получении языка
для моноидальной категории очевидным
изменением будет полное удаление
комбинатора
,
а также добавление двух правил подстановки,
соответствующих шестиугольным уравнениям
(см. подраздел 2.4). При получении языка
для моноидальной категории очевидным
изменением будет полное удаление
комбинатора ![]() и
всех связанных с ним правил подстановки.
Фактически, К. Б. Джей [53] описал язык,
подходящий для замкнутых моноидальных
категорий, в 1989 году; работа С. Амблера
основана на этих результатах.
и
всех связанных с ним правил подстановки.
Фактически, К. Б. Джей [53] описал язык,
подходящий для замкнутых моноидальных
категорий, в 1989 году; работа С. Амблера
основана на этих результатах.
5. Заключение В данной статье было кратко описано, как теория категорий может помочь прояснить наличие аналогов в физике, топологии, логике и теории вычислений. Каждая область знаний по-своему понимает «вещь» (объект) и «процесс» (морфизм), которые организованы в категории, обладающие множеством общих свойств. Для общей картины, в статье изложение было сфокусировано на тех свойствах, которые присутствуют в каждой замкнутой симметричной моноидальной категории. Таблица 4 представляет собой расширенную версию нового Розеттского камня, где показаны некоторые дополнительные аналоги, найденные в процессе изучения.
|
Теория категорий |
Физика |
Топология |
Логика |
Теория вычислений |
|
Объект
|
Гильбертово
пространство
|
Многообразие
|
Высказывание
|
Тип
данных
|
|
Морфизм
|
Оператор
|
Бордизм
|
Доказательство
|
Программа
|
|
Тензорное
произведение объектов
|
Гильбертово
пространство объединённой системы
|
Размеченное
объединение многообразий
|
Конъюнкция
высказываний
|
Произведение
типов данных
|
|
Тензорное
произведение морфизмов
|
Параллельные
процессы
|
Размеченное
объединение бордизмов
|
Доказательства,
проводимые в параллельном режиме
|
Программы,
выполняемые параллельно
|
|
Внутренний
|
Гильбертово
пространство «анти- |
Размеченное
объединение обращённого |
Условное
высказывание
|
Функциональный
тип
|
Таблица 4. Розеттский камень (расширенная версия)
Однако это только попытка вникнуть
в проблему. Можно ещё много рассуждать
о категориях, которые обладают
дополнительными структурами, а также
о том, как их можно использовать для
усиления связей между физикой, топологией,
логикой и теорией вычислений — например,
что произойдёт при переходе от категорий
к ![]() -категориям.
Но подлинное удовольствие возникает,
когда начинается исследование этих
аналогов и новых идей на стыке областей.
Вот пример.
-категориям.
Но подлинное удовольствие возникает,
когда начинается исследование этих
аналогов и новых идей на стыке областей.
Вот пример.
В конце 1980-х годов Э. Уиттен [99] обнаружил, что теория струн оказывается тесно связанной с трёхмерной топологической квантовой теорией поля, а значит, и с теорией узлов и танглов [65]. Это вызвало значительное увеличение числа работ, результаты которых сфокусированы на определённом классе компактных сплетённых моноидальных категорий, называемых «модульными тензорными категориями» [16, 97].
Всё это может выглядеть лишь теорией, в то время как сверхпроводящие тонкие плёнки в магнитном поле фактически дают «частичный квантовый эффект Холла», что может быть чётко смоделировано при помощи подобных категорий [92, 93]. Вкратце, активизация подобных плёнок может действовать как частицы, называемые «анионами». Когда два аниона пересекаются, результат зависит от того, в каком порядке они пересекаются:
Так что наборы анионов описываются объектами в сплетённых моноидальных категориях! Детали зависят от таких факторов, как сила магнитного поля; разнообразие возможностей может быть рассмотрено в рамках модульных тензорных категорий [76, 79].
Пока всё вышеперечисленное относится к физике и топологии. Теория вычислений присоединилась к ним около 2000 года, когда М. Фридман, А. Китаев, М. Ларсен и З. Ванг [41] показали, что некоторые системы анионов могут действовать в качестве «универсальных квантовых компьютеров». Это значит, что, в принципе, произвольные вычисления могут быть произведены при помощи перемещения анионов друг относительно друга. Практическая же реализация не так проста. Тем не менее, компания Майкрософт запустила проект Project Q, в рамках которого делаются попытки выполнить эту задачу. Получение работающего квантового компьютера будет иметь огромную практическую ценность.
Но независимо от того, будут ли квантовые компьютеры когда-либо созданы на практике, результаты — удивительны. Простая диаграмма, как, например:
теперь может рассматриваться в качестве квантового процесса, тангла или вычисления — или просто абстрактного морфизма в произвольной сплетённой моноидальной категории! Это просто один из видов объектов в общей теории систем и процессов.
