
- •02 Марта 2009
- •1. Введение
- •2. Точки пересечения физики и топологи
- •2.1. Теоретические основы
- •2.2. Категории
- •2.3. Моноидальные категории
- •2.4. Сплетённые моноидальные категории
- •2.5. Симметричные моноидальные категории
- •2.6. Замкнутые категории
- •3.1. Теоретические основы
- •3.2. Доказательства как морфизмы
- •4. Теория вычислений
- •4.1. Теоретические основы
- •Благодарности
- •Список литературы
2.2. Категории
Теория категорий была создана около 1945 года, когда С. Эйленберг и С. Маклейн [40] определили понятия «категория», «функтор» между категориями и «естественное преобразование» между функторами. В настоящее время имеется множество введений в теорию [34, 72, 75], включая некоторые, свободно доступные в сети Интернет [20, 46]. Тем не менее, здесь будут приведены некоторые основы.
Определение 1. Категория ![]() состоит
из:
состоит
из:
-
совокупности объектов, при этом если
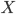 является
объектом
является
объектом 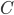 ,
то это записывается как
,
то это записывается как 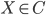 ;
; -
множеств
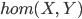 морфизмов
из
морфизмов
из 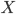 в
в 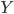 для каждой пары объектов
для каждой пары объектов 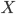 и
и 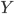 .
Такие множества обозначаются как
.
Такие множества обозначаются как 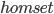 .
.
Если ![]() ,
то этот факт можно записать как
,
то этот факт можно записать как ![]() .
Для
перечисленных компонентов категории
выполняются следующие правила:
.
Для
перечисленных компонентов категории
выполняются следующие правила:
-
Для произвольного объекта
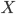 существует
тождественный морфизм
существует
тождественный морфизм 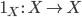 .
. -
Морфизмы можно подвергать композиции: при наличии
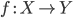 и
и 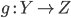 имеет
место композиция морфизмов
имеет
место композиция морфизмов 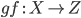 ,
которая также иногда записывается
как
,
которая также иногда записывается
как  .
. -
Тождественный морфизм является одновременно левой и правой единицей относительно операции композиции, то есть, если
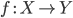 ,
то
,
то 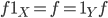 .
. -
Операция композиции ассоциативна, то есть
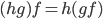 для
произвольных морфизмов
для
произвольных морфизмов  ,
,  и
и  .
.
Определение 2. Морфизм ![]() называется
изоморфизмом, если у него есть обратный
морфизм, то есть существует морфизм
называется
изоморфизмом, если у него есть обратный
морфизм, то есть существует морфизм ![]() такой,
что
такой,
что ![]() и
и ![]() .
.
Категория является простейшей конструкцией, позволяющей описывать системы (объекты) и процессы (морфизмы). Для большей наглядности можно использовать наиболее упрощённые диаграммы Фейнмана. Применимо к линейной алгебре подобные диаграммы часто называются «сплетёнными сетями», а специалисты по теории категорий называют их «струнными диаграммами»; последний термин будет использоваться в настоящей статье. Термин «струна» в данном случае не имеет отношения к теории струн, дело в том, что объекты категории обозначаются как «струны» или «проволочки»:
![]()
а морфизмы
![]() обозначаются
как «чёрные ящики», в которые входит
струна типа
обозначаются
как «чёрные ящики», в которые входит
струна типа ![]() и
выходит струна типа
и
выходит струна типа ![]() :
:
![]()
Композиция двух морфизмов осуществляется
при присоединении выхода одного «чёрного
ящика» ко входу другого. Таким образом,
композиция морфизмов ![]() и
и ![]() выглядит
следующим образом:
выглядит
следующим образом:
![]()
Ассоциативность операции композиции в данном случае подразумевается:
![]()
Данная совокупность условных знаков
обозначает и ![]() ,
и
,
и ![]() .
Таким же образом, если изобразить
тождественный морфизм
.
Таким же образом, если изобразить
тождественный морфизм ![]() в
виде струны, помеченной объектом
в
виде струны, помеченной объектом ![]() :
:
![]()
то в этом случае правила для левой и правой единицы также подразумеваются.
Существует бесконечное количество примеров категорий, но в данной статье будут рассмотрены лишь четыре:
-
 —
категория множеств.
—
категория множеств. -
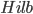 —
категория конечномерных гильбертовых
пространств.
—
категория конечномерных гильбертовых
пространств. -
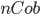 —
категория, морфизмами которой
являются
—
категория, морфизмами которой
являются 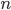 -мерные
бордизмы.
-мерные
бордизмы. -
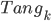 —
категория, морфизмами которой являются
—
категория, морфизмами которой являются
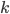 -коразмерные
танглыТеория танглов — один из разделов
теории узлов — прим. перев. .
-коразмерные
танглыТеория танглов — один из разделов
теории узлов — прим. перев. .
Как будет ясно в дальнейшем, все четыре
упомянутых категории являются замкнутыми
симметричными моноидальными категориями,
по крайней мере в случае, если ![]() достаточно
велико. Однако наиболее известная
категория — категория
достаточно
велико. Однако наиболее известная
категория — категория
![]() —
несколько отличается от остальных,
поскольку она является декартовой.
—
несколько отличается от остальных,
поскольку она является декартовой.
По сложившейся традиции, в центре
внимания математиков была категория
![]() ,
в которой объектами являются множества,
а морфизмами функции. Таким образом,
при изучении систем и процессов в физике
очень заманчивым является представление
системы в качестве множества состояний,
а процессов в виде функции перехода из
состояния одной системы в состояние
другой.
,
в которой объектами являются множества,
а морфизмами функции. Таким образом,
при изучении систем и процессов в физике
очень заманчивым является представление
системы в качестве множества состояний,
а процессов в виде функции перехода из
состояния одной системы в состояние
другой.
Однако в квантовой физике учёные используют категорию, в которой объектами являются гильбертовы пространства, а морфизмами — связанные линейные операторы. Система определяется при помощи задания гильбертова пространства, но такое гильбертово пространство не является в точности множеством состояний системы, поскольку состоянием системы является траектория в гильбертовом пространстве. Таким же образом связанный линейный оператор не является в точности функцией перехода из состояния одной системы в состояние другой системы.
Когда же дело касается практической
деятельности в области квантовой физики,
реальное значение имеют не состояния
и функции между ними, а гильбертово
пространство и операторы. Одним из
достоинств теории категорий является
то, что она освобождает исследователя
от «![]() -центристского»
взгляда на традиционную математику и
позволяет применять в квантовой физике
её собственные термины. Как будет
показано, это позволит представить
затруднения, всегда возникающие при
попытке понять квантовый мир, в ином
освещении [11].
-центристского»
взгляда на традиционную математику и
позволяет применять в квантовой физике
её собственные термины. Как будет
показано, это позволит представить
затруднения, всегда возникающие при
попытке понять квантовый мир, в ином
освещении [11].
Чтобы избежать спорных моментов, которые
могут завести обсуждение далеко в
сторону, далее объектами категории ![]() будут считаться конечномерные
гильбертовы пространства, а морфизмами
— линейные операторы (которые в
данном случае автоматически являются
связанными). Конечномерные гильбертовы
пространства достаточно удобны для
целей изложения; бесконечномерные
гильбертовы пространства в определённых
случаях очень важны, но их использование
потребует некоторых существенных
дополнений к идеям, которые будут
обсуждены в статье.
будут считаться конечномерные
гильбертовы пространства, а морфизмами
— линейные операторы (которые в
данном случае автоматически являются
связанными). Конечномерные гильбертовы
пространства достаточно удобны для
целей изложения; бесконечномерные
гильбертовы пространства в определённых
случаях очень важны, но их использование
потребует некоторых существенных
дополнений к идеям, которые будут
обсуждены в статье.
В физике также используются категории,
в которых объекты представляют собой
выбор пространств, а морфизмы —
выбор пространства-времени. Простейшей
такой категорией является категория ![]() ,
где объектами являются (
,
где объектами являются (![]() )-мерные
многообразия, а морфизмами —
)-мерные
многообразия, а морфизмами — ![]() -мерные
бордизмы. Если не учитывать некоторые
тонкости, которые подробно рассмотрены
в иных работах [81], бордизм
-мерные
бордизмы. Если не учитывать некоторые
тонкости, которые подробно рассмотрены
в иных работах [81], бордизм ![]() представляет
собой
представляет
собой ![]() -мерное
многообразие, границей которого является
размеченное объединение (
-мерное
многообразие, границей которого является
размеченное объединение (![]() )-мерных
многообразий
)-мерных
многообразий ![]() и
и ![]() .
Вот несколько бордизмов в случае
.
Вот несколько бордизмов в случае ![]() :
:
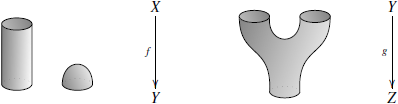
Композиция бордизмов осуществляется
при помощи «склеивания» «входа» одного
из них с «выходом» другого. Так, в
предыдущем примере композиция
бордизмов ![]() имеет
вид:
имеет
вид:
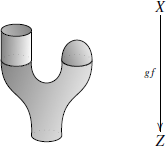
Не менее важна в физике категория,
объектами которой являются совокупности
частиц, а морфизмами — мировые
линии и их взаимодействия.
Диаграммы Фейнмана представляют собой
классический пример, однако «рёбра» на
этих диаграммах нельзя воспринимать
как траектории частиц. В качестве
примера, тесно связанного с топологией,
можно привести категорию ![]() .
.
Грубо говоря, объектом в категории ![]() является
набор точек в гиперкубе размерности
является
набор точек в гиперкубе размерности ![]() ,
в то время как морфизмами являются
«танглы» — наборы дуг и замкнутых
кривых, гладко вписанных в гиперкуб
размерности
,
в то время как морфизмами являются
«танглы» — наборы дуг и замкнутых
кривых, гладко вписанных в гиперкуб
размерности
![]() так,
что замкнутые кривые полностью вписаны
в гиперкуб, а дуги касаются граней только
своим началом и концом и начинаются
только на верхней или на нижней грани
гиперкуба. Если быть более точным, то
танглы — это «изотопические классы»
таких вложенных дуг и замкнутых кривых,
то есть для них важна топология, а не
геометрия. Композиция танглов
осуществляется присоединением нижней
стороны одного гиперкуба к верней
стороне другого.
так,
что замкнутые кривые полностью вписаны
в гиперкуб, а дуги касаются граней только
своим началом и концом и начинаются
только на верхней или на нижней грани
гиперкуба. Если быть более точным, то
танглы — это «изотопические классы»
таких вложенных дуг и замкнутых кривых,
то есть для них важна топология, а не
геометрия. Композиция танглов
осуществляется присоединением нижней
стороны одного гиперкуба к верней
стороне другого.
Более точные определения можно найти
во многих источниках, по крайней мере
для ![]() ,
что даёт танглы в трёхмерном кубе [42,
58, 81, 89, 97, 101]. Но поскольку лучше один раз
увидеть, чем сто раз услышать, ниже
приводится схематичное изображение
морфизма в категории
,
что даёт танглы в трёхмерном кубе [42,
58, 81, 89, 97, 101]. Но поскольку лучше один раз
увидеть, чем сто раз услышать, ниже
приводится схематичное изображение
морфизма в категории ![]() :
:
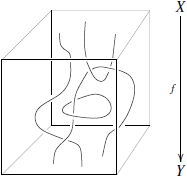
Стоит отметить, что морфизм в
категории ![]() можно
воспринимать как одномерный бордизм,
вложенный в
можно
воспринимать как одномерный бордизм,
вложенный в ![]() -мерный
гиперкуб. Именно поэтому в некоторых
отношениях категории
-мерный
гиперкуб. Именно поэтому в некоторых
отношениях категории ![]() и
и ![]() ведут
себя одинаково.
ведут
себя одинаково.
К следующим двум морфизмам в категории ![]() ,
можно применить операцию композиции:
,
можно применить операцию композиции:
В результате композиции получается:

Поскольку важна только топология танглов, полученный прямоугольник можно сжать в квадрат, если необходимо.
Целесообразно рассматривать танглы,
обладающие дополнительными возможностями.
Например, в «ориентированном» тангле
каждая дуга и замкнутая кривая имеет
направление (ориентацию). Это может быть
показано при помощи маленькой стрелки
на каждой линии диаграммы. Применимо к
физике линии соответствуют мировым
линиям частиц, а стрелки обозначают
направление движения частицы во времени,
согласно утверждению Р. Фейнмана, что
античастицы — это частицы, движущиеся
назад во времени. Также можно рассмотреть
«фреймовые» танглы, в которых каждая
кривая заменяется «лентой». Применимо
к физике это даёт возможность описать
вращение каждой частицы, что особенно
важно для фермионов, которые при спине
![]() ведут
себя нетривиально.
В математическом понимании самыми
подходящими для описания танглами
являются ориентированные фреймовые
танглы [13, 89], поэтому именно они будут
использованы при определении категории
ведут
себя нетривиально.
В математическом понимании самыми
подходящими для описания танглами
являются ориентированные фреймовые
танглы [13, 89], поэтому именно они будут
использованы при определении категории ![]() .
У категории
.
У категории
![]() также
есть ориентированная фреймовая версия,
но данный факт впоследствии не будет
иметь большого значения.
также
есть ориентированная фреймовая версия,
но данный факт впоследствии не будет
иметь большого значения.
Сложно оперировать категориями без отображения между ними. Отображение между категориями называется «функтором»:
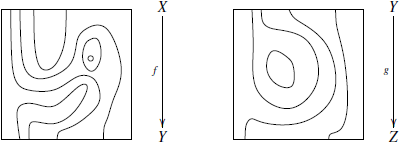
Определение 3. Функтор ![]() из
категории
из
категории ![]() в
категорию
в
категорию ![]() является
отображением, которое:
является
отображением, которое:
-
Отображает каждый объект
 в
некоторый объект
в
некоторый объект  .
. -
Отображает каждый морфизм
 из
категории
из
категории 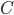 в морфизм
в морфизм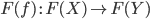 в
категории
в
категории 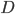 .
.
Функтор должен удовлетворять следующим условиям:
-
Для всех объектов
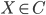 функтор
сохраняет тождественные морфизмы:
функтор
сохраняет тождественные морфизмы: 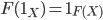 .
. -
Для произвольной пары морфизмов из категории
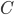 функтор
сохраняет композицию:
функтор
сохраняет композицию: 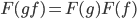 .
.
В последующих разделах будет показано,
что функторы и естественные преобразования
удобны для наложения на категории
дополнительных структур. Функтор ![]() можно также трактовать как «представление»
категории
можно также трактовать как «представление»
категории ![]() в
в
![]() .
Смысл заключается в том, что функтор
.
Смысл заключается в том, что функтор ![]() может
отображать объекты и морфизмы некоторой
«абстрактной» категории
может
отображать объекты и морфизмы некоторой
«абстрактной» категории ![]() в
объекты и морфизмы некоторой более
«конкретной» категории
в
объекты и морфизмы некоторой более
«конкретной» категории ![]() .
.
Например, можно рассмотреть абстрактную
группу ![]() .
Это то же самое, что и категория, состоящая
из одного объекта, все морфизмы которой
обратимы. Объект в данном случае интереса
не представляет, поэтому его можно
просто обозначить
.
Это то же самое, что и категория, состоящая
из одного объекта, все морфизмы которой
обратимы. Объект в данном случае интереса
не представляет, поэтому его можно
просто обозначить ![]() ,
но морфизмы — это элементы
,
но морфизмы — это элементы ![]() ,
их композиция осуществляется при помощи
операции умножения в группе. Тогда
представление группы
,
их композиция осуществляется при помощи
операции умножения в группе. Тогда
представление группы ![]() на
конечномерное гильбертово пространство
— это то же самое, что и функтор
на
конечномерное гильбертово пространство
— это то же самое, что и функтор ![]() .
Таким же образом, действие группы
.
Таким же образом, действие группы ![]() на
множество — это то же самое, что и
функтор
на
множество — это то же самое, что и
функтор ![]() .
В обоих случаях абстрактная группа
становится более конкретной.
.
В обоих случаях абстрактная группа
становится более конкретной.
Со времени опубликования диссертации
Ф. В. Лоувера по функциональной семантике
в 1963 году [69], понимание функторов в
качестве представлений стало доминирующим.
Однако в разных областях различна и
терминология. Вслед за Ф. В. Лоувером,
логики обычно называют категорию ![]() «теорией»,
а функтор
«теорией»,
а функтор ![]() называют
«моделью» этой теории. Другие математики
могут называть функтор
называют
«моделью» этой теории. Другие математики
могут называть функтор ![]() «алгеброй»
теории. В данной работе под категорией
«алгеброй»
теории. В данной работе под категорией
![]() будет
пониматься категория
будет
пониматься категория ![]() .
.
В физике функтор ![]() называется
«теорией». Тогда под категорией
называется
«теорией». Тогда под категорией ![]() будет пониматься либо введённая ранее
категория
будет пониматься либо введённая ранее
категория ![]() ,
либо похожая категория бесконечномерных
гильбертовых пространств. Например, и
«конформные теории поля» [85], и
топологические квантовые теории поля
[8] могут рассматриваться в качестве
функторов этого вида.
,
либо похожая категория бесконечномерных
гильбертовых пространств. Например, и
«конформные теории поля» [85], и
топологические квантовые теории поля
[8] могут рассматриваться в качестве
функторов этого вида.
Если трактовать функторы как модели, то естественные преобразования являются отображениями между моделями:
Определение 4. Для заданных
функторов ![]() естественное
преобразование
естественное
преобразование ![]() сопоставляет
с каждым объектом
сопоставляет
с каждым объектом ![]() морфизм
морфизм ![]() такой,
что для произвольного морфизма
такой,
что для произвольного морфизма ![]() в
категории
в
категории ![]() уравнение
уравнение ![]() выполняется
в категории
выполняется
в категории ![]() .
Другими словами, следующая диаграмма
является коммутативной:
.
Другими словами, следующая диаграмма
является коммутативной:
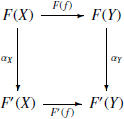
(Переход сначала вправо, а потом вниз даёт тот же результат, что и переход сначала вниз, а потом вправо).
Определение 5. Естественным
изоморфизмом между функторами ![]() называется
такое естественное преобразование
называется
такое естественное преобразование ![]() ,
что
,
что ![]() является
изоморфизмом для каждого объекта
является
изоморфизмом для каждого объекта ![]() .
.
Например, пусть ![]() —
функторы, причём категория
—
функторы, причём категория ![]() является
группой, то есть категорией с одним
объектом, например
является
группой, то есть категорией с одним
объектом, например ![]() .
Тогда, как уже было сказано,
функторы
.
Тогда, как уже было сказано,
функторы ![]() и
и ![]() являются
представлениями группы
являются
представлениями группы ![]() в
гильбертовых пространствах
в
гильбертовых пространствах ![]() и
и ![]() .
Естественным преобразованием
.
Естественным преобразованием ![]() в
данном случае является переплетающий
оператор из одного представления
в другое, то есть линейный оператор
в
данном случае является переплетающий
оператор из одного представления
в другое, то есть линейный оператор ![]() ,
который удовлетворяет условию
,
который удовлетворяет условию ![]() для
всех элементов группы
для
всех элементов группы ![]() .
.
