3.1. Теоретические основы

Симметричные моноидальные замкнутые категории встречаются не только в физике и топологии, но также и в логике, и данный раздел пояснит, почему. Для начала стоит изложить некоторые идеи логики. Современные специалисты в области логики изучают различные системы суждений, выходящие за рамки классической логики. Естественно, что даже в классической логике выделяют несколько ступеней сложности. Вначале идёт «исчисление высказываний», которое работает с абстрактными высказываниями , ,  и т. д. при помощи следующих логических связок:

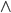•  — конъюнкция, логическое «И».

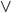•  — дизъюнкция, логическое «ИЛИ».

•  — импликация, логическое «ЕСЛИ-ТО».

•  — отрицание, логическое «НЕ».

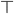•  — логическое значение истинности «ИСТИНА».

•  — логическое значение истинности «ЛОЖЬ».

Следующим идёт «исчисление предикатов», где используются переменные вроде , ,  и т. д., предикаты типа  и , а также квантор всеобщности («для всех»)  и квантор существования («существует») , которые позволяют квантифицировать переменные. Имеются и высшие ступени, позволяющие квантифицировать предикаты, и т. д. Авторы рассматривают только исчисление высказываний. Но даже в нём имеется множество вариантов «классической версии». Большинство изучаемых вариантов менее строги по сравнению с классической версией: в них становится сложнее или даже невозможно доказать некоторые вещи, которые в классической обычно принимаются на веру. Причиной является то, что некоторые логики отрицают возможность доказательства определённых известных принципов. Но имеются и другие причины. Одна из них заключается в том, что изучение менее строгих систем позволяет точно определить, какие методы суждения необходимо использовать для получения тех или иных результатов. Ещё одна причина, представляющая больший интерес в контексте данной статьи, заключается в том, что удаление известных принципов и последующее добавление их в систему по одному позволяет пролить свет на связь между логикой и теорией категорий.

К примеру, около 1907 года Л. Э. Я. Брауэр [49] начал выступать в защиту «интуиционизма». В частности, он поставил под сомнение верность закона исключённого третьего, утверждающего, что из высказывания  можно вывести высказывание . Одна из проблем состоит в том, что доказательства с использованием данного закона не являются «конструктивными». Например, можно доказать от противного, что некоторое уравнение имеет решение, однако будет непонятно, как такое решение получить. Для Л. Э. Я. Брауэра это обозначало, что закон неверен.

Каждому, кто считает, что закон исключённого третьего неверен, просто необходимо изучить интуиционистскую логику. Но имеется и другая причина для её изучения. А именно: ничего не теряется при удалении закона исключённого третьего из перечня постулатов. Вместо него появляется чёткое разграничение между двумя видами доказательств: прямого доказательства высказывания  и доказательства от противного, которое требует . Если необходимость применять данное разграничение отсутствует, то его можно игнорировать.

В 1930-х годах К. Гёдель [45] и Г. Гентцен [94] показали, что классическая логика может быть встроена в интуиционистскую. Фактически они нашли оператор, который переводит произвольную формулу  исчисления высказываний в формулу  так, что формула  доказуема классически тогда и только тогда, когда формула  доказуема интуиционистски. (Что ещё больше впечатляет, вышеупомянутый оператор также работает с исчислением предикатов).

Позже появился другой повод заинтересоваться интуиционистской логикой — её связь с теорией категорий. В своём простейшем проявлении такая связь работает следующим образом. Путь есть набор высказываний , ,  и т. д., которые подчиняются законам интуиционистского исчисления высказываний. Можно создать категорию , в которой объектами являются данные высказывания, и существует не более одного морфизма из одного произвольного объекта  в другой произвольный объект , а именно единственный морфизм  («из  следует »), и никакой другой!

Категория, в которой существует не более одного морфизма между двумя произвольными объектами, называется предпорядком. В исчислении высказываний два высказывания часто объявляются эквивалентными, если из первого можно вывести второе, а из второго первое. Тогда имеет место особый вид предпорядка: в нём изоморфные объекты автоматически эквивалентны. Этот особой вид предпорядка называется частично упорядоченным множеством, или ЧУМ для краткости. ЧУМ встречаются в логике в большом количестве, поскольку представляют собой простую конструкцию для понимания импликации.

Если начать со множества высказываний, которые подчиняются правилам интуиционистского исчисления высказываний, то конечная категория  будет лучше, чем простое ЧУМ. Она также является декартовой, где умножением высказываний  и  является , а финальным объектом — . Чтобы это увидеть, необходимо иметь в виду, что произвольное высказывание  обладает уникальным морфизмом для  всякий раз, когда обладает морфизмами для высказываний  и  по отдельности. По сути, это выражение факта, что из  следует  тогда и только тогда, когда из  следуют и , и . Но с использованием терминов теории категорий. Легко заметить, что  является финальным объектом, поскольку ИСТИНА следует из любого высказывания.

Более того, категория  является замкнутой декартовой категорией, в которой  представляет собой внутренний -функтор. Причина в том, что из следует  тогда и только тогда, когда из  следует . Это условие автоматически влечёт за собой базовое свойство внутреннего -функтора, то есть . Конечно, может возникнуть вопрос:  «В чём разница между «из  следует » и  ?» Его необходимо объяснить более подробно: первое выражение использует множество , в котором имеется один элемент в случае, если из  следует , и ни одного в противном случае; второе выражение является внутренним -множеством, объектом в категории .

Таким образом,  является декартово замкнутым ЧУМ. Однако у него имеется ещё одно замечательно свойство, которое проявляется благодаря наличию  и . Было показано, что  и  делают категорию  декартовой;  и  удовлетворяют аналогичным правилам, однако с обращённой импликацией, так что они превращают категорию  в декартову.

В частности, отрицание ничего дополнительного не даёт, поскольку можно определить  как , и такое определение будет удовлетворять всем законам интуиционистского исчисления высказываний. Так что тип категорий, который получается из интуиционистского исчисления высказываний, где высказывания являются объектами, а импликации — морфизмами, — это в точности алгебра Гейтинга: замкнутое декартово ЧУМ , для которого  также является замкнутым декартовым ЧУМ.

А. Гейтинг, ученик Л. Э. Я. Брауэра, представил алгебры Гейтинга в рамках интуиционистской логики ещё до того, как был разработан аппарат теории категорий. Так что он использовал совершенно другую форму их представления. Однако теоретико-категориальный подход к алгебрам Гейтинга иллюстрирует связь между замкнутыми декартовыми категориями и логикой и также подтверждает тот факт, что случаи с игнорированием закона исключённого третьего представляют интерес для изучения.

Ранее были описаны основные черты замкнутых декартовых категорий, однако ничего не говорилось о случаях, когда двойственная к декартовой категория также является замкнутой декартовой категорией. В связи с этим в дальнейшем материал по логике будет несколько ограничен,  авторы не станут рассматривать  и , но сконцентрируют внимание только на фрагменте логики, который включает в себя ,  и .

Даже в этом случае найдутся интересные темы для обсуждения и занятные способы изменения стандартных правил, о чём и пойдёт речь в дальнейшем. Но прежде — пара слов о теории доказательств.

Теория доказательств — раздел математической логики, где доказательства являются объектами изучения. Данная теория позволяет более подробно рассмотреть исчисление высказываний, поскольку предлагает рассматривать не только вопрос следует ли или нет из некоторого предположения  заключение , но всё множество доказательств, ведущих от  к . Это позволяет изучать не только ЧУМ (или предпорядки), но категории, в которых разрешено наличие нескольких морфизмов от одного объекта к другому.

В подходе Д. Гильберта к доказательству имеется множество постулатов и одно правило вывода, а именно Modus ponens, то есть правило, на основании которого из истинности высказывания  и наличия импликации  можно заключить истинность . Большинство современных теорий доказательств фокусируются на другом подходе, называемом «исчислением последовательностей»Иногда используется термин «исчисление секвенций» — прим. перев. , введённом Г. Гентценом [94]. В этом подходе имеется небольшое количество постулатов и множество правил вывода.

Отличным введением в исчисление последовательностей является книга «Доказательства и типы» Ж.-И. Жирара, И. Лафонта и П. Тейлора, бесплатно доступная в сети Интернет [44]. В настоящей работе она будет процитирована с некоторыми примечаниями. «Последовательностью» называется нечто, вроде следующего: , где  и  являются высказываниями. Приведённая запись говорит, что если имеется последовательность всех высказываний , взятых вместе, то они могут использоваться для доказательства по крайней мере одного высказывания . Это условие хоть и странно выглядит, но придаёт исчислению последовательностей симметричность, как будет показано далее.

В исчислении последовательностей «правилом вывода» называется нечто, что производит новые последовательности из уже имеющихся. Например, вот правило левого ослабления:

Запись говорит о том, что если имеется последовательность, показанная над горизонтальной линией, то из неё можно получить последовательность, показанную под этой линией. В данном случае можно добавлять дополнительные высказывания  без какого-либо ущерба. Благодаря условию, о котором было упомянуто, у данного правила существует зеркально отражённое, называемое правилом правого ослабления:

Фактически, у всех правил Гентцена имеются зеркальные отражения! Например, вот правило, называемое левым сокращением:

У данного правила есть зеркально отражённое, называемое правым сокращением:

Также у правила для операции :

есть зеркально отражённое для операции :

Специалисты по логике заметили, что данная зеркальная симметрия может быть рассмотрена в понятиях дуальности между категорией и двойственной категорией.

Г. Гентцен использовал последовательности для записи правил вывода в классическом исчислении высказываний и классическом исчислении предикатов. Теперь в этих формах логики имеет место истинность  тогда и только тогда, когда . Почему Г. Гентцен использовал последовательности с перечислением высказываний по обе стороны символа , а не просто высказывания? Причина в том, что это позволило ему использовать только такие правила вывода, у которых имеется «свойство подформулы», которое утверждает, что каждое высказывание, находящееся над горизонтальной линией, встречается как часть некоторого высказывания под линией. Так что доказательство, построенное по таким правилам вывода, становится «деревом», на котором все верхние высказывания являются подформулами нижних.

Правила вывода со свойствами подформулы впоследствии были ещё раз применены. Например, в 1936-м году Г. Гентцен получил возможность доказать непротиворечивость системы постулатов арифметики Пеано! Его доказательство основывалось на индукции по деревьям (читатели, знакомые с второй теоремой К. Гёделя о неполноте, могут быть уверены, что такой тип индукции сам по себе не может быть применён в рамках арифметики Пеано).

Наиболее известным правилом вывода, которое не имеет свойства подформулы, является «правило сечения»:

Из двух последовательностей над горизонтальной чертой при применении данного правила получается одна последовательность, расположенная под чертой. Необходимо отметить, что промежуточное высказывание  отсутствует в последовательности под чертой. Оно «отсечено». Таким образом, правило сечения не имеет свойства подформулы. Однако одно из выдающихся достижений Г. Гентцена заключается в следующем: любое доказательство в классическом исчислении высказываний (и даже исчислении предикатов), полученное при помощи правила сечения, может быть получено и без него. Это называется процессом «удаления сечения».

Г. Гентцен также составил набор правил, которые подходят для интуиционистских исчислений высказываний и предикатов. В этих правилах нет зеркальной симметричности, как в классическом случае. Однако в 1980-х годах симметричность была восстановлена, когда Ж.-И. Жирар открыл «линейную логику» [43].

Линейная логика позволяет учитывать то, сколько раз какое-либо утверждение используется при достижении заданного заключения. Для получения данного свойства Ж.-И. Жирар ввел несколько новых логических связок: для начала — «линейные» связки, обозначенные как  и , а также логическую константу . Новые связки работают примерно так же, как и ,  и . Однако они соответствуют правилам симметричной моноидальной категории, а не замкнутой декартовой категории. В частности, при помощи высказывания  невозможно доказать ни , ни . Так что нельзя свободно «дублировать» или «удалять» высказывания при помощи этих связок, что нашло своё отражение в линейной логике, где отсутствуют правила ослабления и сокращения Гентцена.

Применение данных связок предполагает опредлённые ограничения, но Ж.-И. Жирар одновременно сохранил связки ,  и , которые удовлетворяют обычным правилам. Он также ввёл оператор, названный «экспоненциальным», — , который получает высказывание  и преобразует его в «набор копий высказывания  произвольного размера». Так, например, из  можно доказать следующие высказывания: , само по себе , ,  и т. д.

В полноценной линейной логике имеется даже больше связок, чем описано в данном разделе. На первый взгляд она выглядит вычурной и своеобразной, и существует две её версии — классическая и интуиционистская! Но как классическая логика может быть встроена в интуиционистскую, так и интуиционистская логика может быть встроена в интуиционистскую линейную логику [43]. Так что при этом не теряется дедуктивная сила и появляется возможность провести более тонкие различия.

В дальнейшем речь пойдёт об интуиционистской логике, в которой имеются связки  ,  и . Этот фрагмент называется «мультипликативной интуиционистской линейной логикой» [48, 82] и, похоже, является системой, подходящей для замкнутых симметричных моноидальных категорий — не больше, не меньше.