
- •02 Марта 2009
- •1. Введение
- •2. Точки пересечения физики и топологи
- •2.1. Теоретические основы
- •2.2. Категории
- •2.3. Моноидальные категории
- •2.4. Сплетённые моноидальные категории
- •2.5. Симметричные моноидальные категории
- •2.6. Замкнутые категории
- •3.1. Теоретические основы
- •3.2. Доказательства как морфизмы
- •4. Теория вычислений
- •4.1. Теоретические основы
- •Благодарности
- •Список литературы
2.3. Моноидальные категории
В физике часто удобно представлять две соприкасающиеся друг с другом системы как новую единую систему. В топологии размеченное объединение двух многообразий само по себе является многообразием. В логике конъюнкция двух высказываний также является высказыванием. В программировании можно комбинировать два типа данных в новый «тип-произведение». Понятие «моноидальная категория» объединяет все перечисленные примеры.
В моноидальной категории ![]() имеется
функтор
имеется
функтор ![]() ,
который принимает на вход два объекта
,
который принимает на вход два объекта ![]() и
и ![]() ,
комбинирует их и возвращает новый
объект
,
комбинирует их и возвращает новый
объект ![]() .
Для большей точности необходимо ввести
понятие декартова произведения категорий:
.
Для большей точности необходимо ввести
понятие декартова произведения категорий:
Определение 6. Декартовым
произведением ![]() категорий
категорий ![]() и
и ![]() называется
категория, в которой:
называется
категория, в которой:
-
Объектами являются пары
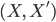 ,
состоящие из
,
состоящие из 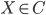 и
и 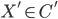 .
. -
Морфизм из
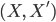 в
в 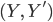 представляет
собой пару
представляет
собой пару 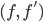 ,
где
,
где 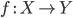 и
и 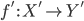 .
. -
Композиция производится покомпонентно:
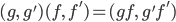 .
. -
Тождественный морфизм также определяется покомпонентно:
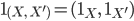 .
.
С. Маклейн [71] дал определение моноидальной
категории в 1963 году. Нюанс определения
заключается в том, что выражения ![]() и
и ![]() обычно
не равны между собой. Между ними следует
построить изоморфизм, называемый
«ассоциатором». Аналогично, если
моноидальная категория включает в себя
единичный объект
обычно
не равны между собой. Между ними следует
построить изоморфизм, называемый
«ассоциатором». Аналогично, если
моноидальная категория включает в себя
единичный объект ![]() ,
выражения
,
выражения
![]() и
и ![]() обычно не равны исходному объекту
обычно не равны исходному объекту ![]() .
Так же можно определить изоморфизм
.
Так же можно определить изоморфизм ![]() и
и ![]() .
Чтобы выполняться, данные изоморфизмы
должны удовлетворять следующим условиям:
.
Чтобы выполняться, данные изоморфизмы
должны удовлетворять следующим условиям:
Определение 7. Моноидальная категория состоит из:
-
Категории
 .
. -
Функтора тензорного произведения
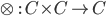 .
. -
Единичного объекта
 .
. -
Естественного изоморфизма, называемого ассоциатором, который сопоставляет с каждой тройкой объектов
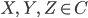 изоморфизм .
изоморфизм . -
Естественных изоморфизмов, называемых левым и правым объединителями, которые сопоставляют каждому объекту
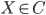 изоморфизмы
изоморфизмы 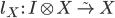 и
и 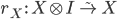 .
.
Для моноидальной категории должны выполняться следующие условия:
-
Для произвольных
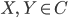 диаграмма, изображенная ниже, коммутативна
(правило треугольника):
диаграмма, изображенная ниже, коммутативна
(правило треугольника):

-
Для произвольных
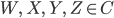 коммутативна следующая диаграмма
(правило пятиугольника):
коммутативна следующая диаграмма
(правило пятиугольника):
Когда имеется тензорное произведение
четырёх объектов, существует пять
способов расставить скобки в выражении,
и на первый взгляд ассоциатор позволяет
построить два изоморфизма из ![]() в
в ![]() ,
однако правило пятиугольника подразумевает,
что эти изоморфизмы эквивалентны. Когда
имеется тензорное произведение большего
количества объектов, то существует ещё
большее количество способов построить
изоморфизмы при помощи ассоциатора.
Однако С. Маклейн показал, что
эквивалентность таких изоморфизмов
следует из правила пятиугольника.
Аналогично правило треугольника
позволяет утверждать, что все изоморфизмы,
построенные при помощи ассоциатора и
левых и правых объединителей, эквивалентны
между собой.
,
однако правило пятиугольника подразумевает,
что эти изоморфизмы эквивалентны. Когда
имеется тензорное произведение большего
количества объектов, то существует ещё
большее количество способов построить
изоморфизмы при помощи ассоциатора.
Однако С. Маклейн показал, что
эквивалентность таких изоморфизмов
следует из правила пятиугольника.
Аналогично правило треугольника
позволяет утверждать, что все изоморфизмы,
построенные при помощи ассоциатора и
левых и правых объединителей, эквивалентны
между собой.
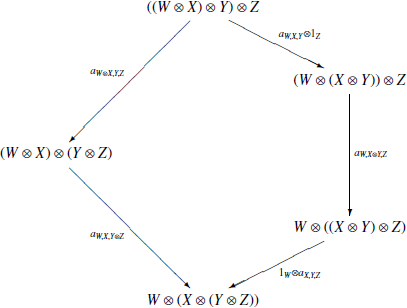
В моноидальной категории процессы могут
выполняться в «параллельном» или
«последовательном» режимах. Выполнение
процессов в последовательном режиме —
просто композиция морфизмов, что имеется
в любой категории. Но в моноидальной
категории можно тензорно перемножить
морфизмы ![]() и
и ![]() и
получить «параллельный процесс»
и
получить «параллельный процесс» ![]() .
Схематично его можно изобразить
несколькими способами:
.
Схематично его можно изобразить
несколькими способами:
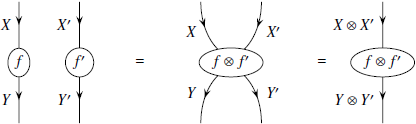
В общем виде произвольный морфизм
можно изобразить в виде чёрного ящика
с ![]() входами
и
входами
и ![]() выходами:
выходами:
Единичный объект ![]() изображается
как пустое место. Тогда морфизм
изображается
как пустое место. Тогда морфизм ![]() изображается
следующим образом:
изображается
следующим образом:
![]()
При помощи композиции и тензорного произведения морфизмов можно изображать сложные схемы, сходные с диаграммами Фейнмана:
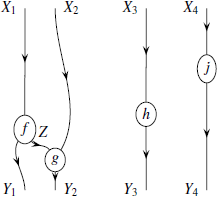
При изображении подобных схем законы моноидальной категории позволяют игнорировать ассоциаторы и объединители. Теорема о когерентности Маклейна утверждает, что произвольная моноидальная категория в определённом смысле «эквивалентна» категории, в которой все ассоциаторы и объединители представляют собой тождественные морфизмы [71].
Также можно произвольным образом изменить изображение, не изменяя морфизмов, которые оно представляет. Например, вышеприведённые морфизмы эквивалентны следующим:
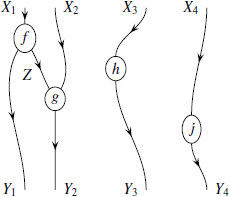
У каждого, кто использует струнные диаграммы для вычислений в моноидальных категориях, возникает вопрос: «Как именно можно изменять изображения, не изменяя морфизмы, которым они соответствуют?» Авторы рекомендуют читателю самостоятельно проверить, что допустимо, а что нет. Например, можно показать, что возможно перемещать «чёрные ящики» вниз и вверх:
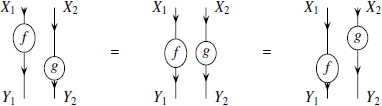
Для более подробного изучения правил изменения диаграмм, стоит обратиться к исходной статье А. Джояла и Р. Стрита [55] и к книге Д. Н. Йеттера [101].
Теперь можно рассмотреть примеры. Ключевой момент состоит в том, что одна и та же категория может быть связана с различными тензорными произведениями, а это приводит к получению иных моноидальных категорий.
-
Существует способ преобразовать категорию
 в
моноидальную категорию. В данном
случае операция
в
моноидальную категорию. В данном
случае операция  представляет
собой декартово произведение
представляет
собой декартово произведение  ,
а единицей является синглетон
(одноэлементное множество). Необходимо
отметить, что данное тензорное
произведение не совсем ассоциативно,
поскольку
,
а единицей является синглетон
(одноэлементное множество). Необходимо
отметить, что данное тензорное
произведение не совсем ассоциативно,
поскольку 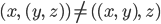 ,
однако имеется естественный
изоморфизм
,
однако имеется естественный
изоморфизм  ,
который является ассоциатором. Похожие
соглашения дают правые и левые
объединители. В моноидальной категории
тензорным произведением
морфизмов
,
который является ассоциатором. Похожие
соглашения дают правые и левые
объединители. В моноидальной категории
тензорным произведением
морфизмов 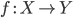 и
и 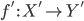 является
функция
является
функция 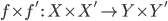 ,
которая переводит пару
,
которая переводит пару 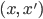 в
пару
в
пару  .
.
Другой способ преобразования категории ![]() в
моноидальную категорию заключается в
том, чтобы принять за операцию
в
моноидальную категорию заключается в
том, чтобы принять за операцию ![]() размеченное
объединение, которое обозначается
как
размеченное
объединение, которое обозначается
как ![]() .
Здесь единицей является пустое множество.
Так же, как и в других примерах, правила
для ассоциативности и для объединителей
слева и справа работают только с точностью
до естественного изоморфизма. В данной
моноидальной категории тензорным
произведением двух морфизмов
.
Здесь единицей является пустое множество.
Так же, как и в других примерах, правила
для ассоциативности и для объединителей
слева и справа работают только с точностью
до естественного изоморфизма. В данной
моноидальной категории тензорным
произведением двух морфизмов ![]() и
и ![]() является
функция
является
функция ![]() ,
которая переводит значение
,
которая переводит значение ![]() в
в ![]() в
случае, если
в
случае, если ![]() ,
и в
,
и в ![]() в
случае, если
в
случае, если ![]() .
.
Тем не менее, в дальнейшем будет
предполагаться, что категория
![]() преобразовывается
в моноидальную категорию при помощи
декартова произведения.
преобразовывается
в моноидальную категорию при помощи
декартова произведения.
-
Есть способ преобразовать категорию
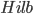 в
моноидальную. Для этого в качестве
тензорного произведения можно
использовать обычное тензорное
произведение гильбертовых пространств:
в
моноидальную. Для этого в качестве
тензорного произведения можно
использовать обычное тензорное
произведение гильбертовых пространств: 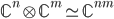 .
Тогда в качестве единичного объекта
.
Тогда в качестве единичного объекта 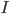 можно
взять одномерное гильбертово пространство,
например
можно
взять одномерное гильбертово пространство,
например
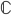 .
.
Другой способ преобразования категории ![]() в моноидальную категорию — принять
операцию прямой суммы в качестве
тензорного произведения:
в моноидальную категорию — принять
операцию прямой суммы в качестве
тензорного произведения: ![]() .
Тогда единичным объектом является
нульмерное гильбертово пространство
.
Тогда единичным объектом является
нульмерное гильбертово пространство ![]() .
.
Тем не менее, в дальнейшем будет
предполагаться, что категория
![]() преобразовывается
в моноидальную категорию при помощи
тензорного произведения.
преобразовывается
в моноидальную категорию при помощи
тензорного произведения.
-
Тензорное произведение объектов и морфизмов в категории
 определяется
размеченным объединением. Например,
тензорное произведение следующих двух
морфизмов:
определяется
размеченным объединением. Например,
тензорное произведение следующих двух
морфизмов:
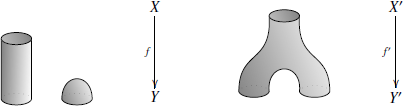
есть следующий морфизм:
-
Категория
 может
быть преобразована в моноидальную для
может
быть преобразована в моноидальную для
![]() ,
при этом тензорное произведение задаётся
как размеченное объединение. Например,
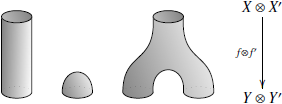
для двух следующих танглов:
,
при этом тензорное произведение задаётся
как размеченное объединение. Например,
для двух следующих танглов:
тензорное произведение выглядит следующим образом:
Вышеприведённый пример с
категорией ![]() отличается
от трёх других примеров, поскольку у
декартова произведения множеств
отличается
от трёх других примеров, поскольку у
декартова произведения множеств ![]() есть функции, называемые «проекциями»
во множества
есть функции, называемые «проекциями»
во множества
![]() и
и ![]() :
:
![]()
У категорий в других примерах
подобные функции отсутствуют, они
появляются только у категории
![]() с
использованием операции
с
использованием операции ![]() .
Кроме того, каждое множество обладает
единственной функцией, переводящей
данное множество в синглетон:
.
Кроме того, каждое множество обладает
единственной функцией, переводящей
данное множество в синглетон:
![]() .
В основных примерах подобная функция
также отсутствует, хотя категория
.
В основных примерах подобная функция
также отсутствует, хотя категория ![]() с
использованием операции
с
использованием операции ![]() обладает проекциями. Удивительная
особенность квантовой механики
заключается в том, что категория
обладает проекциями. Удивительная
особенность квантовой механики
заключается в том, что категория
![]() преобразуется
в моноидальную категорию при помощи
операции
преобразуется
в моноидальную категорию при помощи
операции
![]() ,
вместо
,
вместо ![]() ,
даже несмотря на то, что вторая операция
приводит к получению моноидальной
категории, больше похожей на категорию
,
даже несмотря на то, что вторая операция
приводит к получению моноидальной
категории, больше похожей на категорию ![]() .
.
Можно выделить определённые особенности декартова произведения множеств и его функций-проекций, получив определение, подходящее к любой категории:
Определение 8. Для заданных
объектов ![]() и
и ![]() в
некоторой категории полагается, что
объект
в
некоторой категории полагается, что
объект ![]() ,
ассоциированный с морфизмами
,
ассоциированный с морфизмами ![]() ,
является декартовым произведением
(или просто произведением)
объектов
,
является декартовым произведением
(или просто произведением)
объектов ![]() и
и ![]() ,
если для каждого объекта
,
если для каждого объекта ![]() и
морфизмов
и
морфизмов
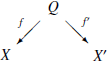
имеет место единственный морфизм ![]() ,
вместе с которым следующая диаграмма
является коммутативной:
,
вместе с которым следующая диаграмма
является коммутативной:
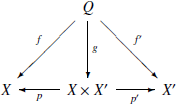
(Таким образом, ![]() и
и ![]() ).
То есть в категории имеет место двоичное
(бинарное) произведение, если каждая
пара элементов обладает произведением.
Произведение может не существовать или
может не быть однозначно
определяемым. Но если оно существует,
то оно однозначно определяемо с
точностью до канонического изоморфизма.
Это позволяет говорить об «определённом»
произведении объектов
).
То есть в категории имеет место двоичное
(бинарное) произведение, если каждая
пара элементов обладает произведением.
Произведение может не существовать или
может не быть однозначно
определяемым. Но если оно существует,
то оно однозначно определяемо с
точностью до канонического изоморфизма.
Это позволяет говорить об «определённом»
произведении объектов ![]() и
и ![]() и
обозначать его как
и
обозначать его как ![]() .
.
Хотя данное определение декартова
произведения достаточно просто, на
первый взгляд оно немного пугает. Для
наглядности стоит рассмотреть пример
комбинирования двух морфизмов ![]() и
и ![]() в
один морфизм
в
один морфизм ![]() .
Определение декартова произведения
объясняет, как построить морфизм
подобного рода из пары морфизмов, то
есть морфизмов из
.
Определение декартова произведения
объясняет, как построить морфизм
подобного рода из пары морфизмов, то
есть морфизмов из ![]() в
объекты
в
объекты ![]() и
и ![]() .
Если обозначить данные морфизмы
как
.
Если обозначить данные морфизмы
как ![]() и
и ![]() ,
то искомым морфизмом будет
,
то искомым морфизмом будет ![]() :
:
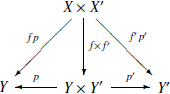
Теперь необходимо выделить свойства одноэлементного множества:
Определение 9. Объект ![]() в
категории
в
категории ![]() называется
финальным (терминальным), если для
произвольного объекта
называется
финальным (терминальным), если для
произвольного объекта ![]() существует
уникальный морфизм из
существует
уникальный морфизм из ![]() в
в ![]() ,
который обозначается как
,
который обозначается как ![]() .
.
Финальный объект также может отсутствовать
и не быть однозначно определяемым, но
он однозначно определяем с точностью
до канонического изоморфизма. Именно
поэтому говорится об «определённом»
финальном объекте категории, который
обозначается специфическим символом ![]() .
.
Ранее было введено понятие бинарного
произведения. Также можно говорить
об ![]() -арном
произведении для других значений
-арном
произведении для других значений ![]() ,
однако категория с существующим бинарным
произведением обладает и другими
произведениями для всех
,
однако категория с существующим бинарным
произведением обладает и другими
произведениями для всех ![]() ,
поскольку их можно создавать в виде
повторяющихся бинарных произведений.
Случай
,
поскольку их можно создавать в виде
повторяющихся бинарных произведений.
Случай ![]() тривиален,
поскольку произведение одного объекта
является этим самым объектом (с точностью
до канонического изоморфизма). Оставшийся
случай — это
тривиален,
поскольку произведение одного объекта
является этим самым объектом (с точностью
до канонического изоморфизма). Оставшийся
случай — это
![]() .
Нуль-арным произведением объектов, если
оно существует, является финальный
(терминальный) объект. Тогда можно
сформулировать следующее определение:
.
Нуль-арным произведением объектов, если
оно существует, является финальный
(терминальный) объект. Тогда можно
сформулировать следующее определение:
Определение 10. Категория имеет конечные произведения, если в ней есть бинарное произведение и финальный (терминальный) объект.
Категория с конечными произведениями
всегда может быть преобразована в
моноидальную категорию при помощи
выбора конкретного произведения ![]() в
качестве тензорного
в
качестве тензорного ![]() и
выбора конкретного финального объекта
в качестве единицы. Моноидальная
категория такой формы называется
декартовой.
и
выбора конкретного финального объекта
в качестве единицы. Моноидальная
категория такой формы называется
декартовой.
В декартовой категории можно «дублировать
и удалять информацию». В более широком
понимании определение декартовых
произведений даёт способ комбинирования
двух морфизмов ![]() и
и ![]() в
морфизм из
в
морфизм из ![]() в
в ![]() .
Если взять
.
Если взять ![]() и
и ![]() и
и ![]() тождественными
морфизмами, то можно получить диагональный
или дублирующий морфизм:
тождественными
морфизмами, то можно получить диагональный
или дублирующий морфизм: ![]() .
Можно проверить, что в категории
.
Можно проверить, что в категории ![]() этот
морфизм отображает произвольный
элемент
этот
морфизм отображает произвольный
элемент ![]() в
пару
в
пару ![]() .
Диаграмма может быть изображена следующим
образом:
.
Диаграмма может быть изображена следующим
образом:
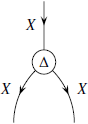
Таким же образом можно обозначить
уникальное отображение в финальный
объект ![]() как удаляющий морфизм и изобразить
его как:
как удаляющий морфизм и изобразить
его как:
![]()
Необходимо отметить, что единица изображается как пустое пространство.
Основным свойством декартова произведения является то, что удвоение какого-либо объекта с последующим удалением самого объекта или его копии не производит никаких действий, что в струнных диаграммах отображается следующим образом:
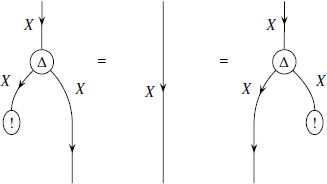
Доказательство предоставляется читателю.
Множество загадочных свойств квантовой
теории связано с тем, что в категории ![]() у обычного тензорного произведения
отсутствует декартово произведение.
Например, в декартовой категории каждый
морфизм вида
у обычного тензорного произведения
отсутствует декартово произведение.
Например, в декартовой категории каждый
морфизм вида
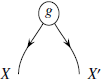
на самом деле имеет следующую форму:
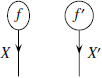
Применимо к категории ![]() это
означает, что каждая точка
множества
это
означает, что каждая точка
множества ![]() происходит
из точек
происходит
из точек ![]() и
и ![]() .
Применимо к физике — что каждое
состояние
.
Применимо к физике — что каждое
состояние ![]() комбинированной
системы
комбинированной
системы ![]() является
комбинацией состояний систем
является
комбинацией состояний систем ![]() и
и ![]() .
Теорема Белла [19] утверждает, что в
квантовой теории данный факт не является
истиной, поскольку квантовая теория
использует недекартову моноидальную
категорию
.
Теорема Белла [19] утверждает, что в
квантовой теории данный факт не является
истиной, поскольку квантовая теория
использует недекартову моноидальную
категорию ![]() .
.
Квантовая теория также не предполагает
возможности свободно дублировать или
удалять информацию. В. К. Вуттерс и В. Х.
Цурек [100] доказали теорему о запрете
клонирования, связанную с этим эффектом,
но данная теорема сфокусирована на
дублировании. Можно также доказать
теорему о запрете удаления, однако
полученные результаты предполагают,
что тензорное произведение в категории ![]() не
является декартовым.
не
является декартовым.
