
- •02 Марта 2009
- •1. Введение
- •2. Точки пересечения физики и топологи
- •2.1. Теоретические основы
- •2.2. Категории
- •2.3. Моноидальные категории
- •2.4. Сплетённые моноидальные категории
- •2.5. Симметричные моноидальные категории
- •2.6. Замкнутые категории
- •3.1. Теоретические основы
- •3.2. Доказательства как морфизмы
- •4. Теория вычислений
- •4.1. Теоретические основы
- •Благодарности
- •Список литературы
2.5. Симметричные моноидальные категории
Иногда переключение двух объектов два раза подряд эквивалентно тому, что с этими объектами вообще ничего не производится. Действительно, знакомая ситуация. Поэтому первые открытые сплетённые категории, были названы «симметричными» [71].
Определение 12. Симметричной
моноидальной категорией называется
сплетённая категория, в которой
переключатель удовлетворяет условию ![]() .
.
Таким образом, в симметричной моноидальной категории имеет место следующее тождество:
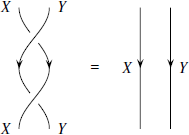
или, что то же самое:
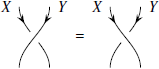
Любая декартова категория автоматически
является симметричной, так что
категория ![]() симметрична.
Также легко можно показать, что
категории
симметрична.
Также легко можно показать, что
категории ![]() и
и ![]() симметричны.
Категория
симметричны.
Категория ![]() симметрична
для
симметрична
для ![]() .
.
Интересен тот факт, что
категория ![]() «стабилизируется»
при
«стабилизируется»
при ![]() —
увеличение значения параметра
—
увеличение значения параметра ![]() выше
значения
выше
значения ![]() даёт
категорию, эквивалентную
даёт
категорию, эквивалентную ![]() .
Причина кроется в том, что в четырёхмерном
пространстве всегда можно развязать
любой узел, а добавление новых измерений
не имеет никакого эффекта. Фактически
категория
.
Причина кроется в том, что в четырёхмерном
пространстве всегда можно развязать
любой узел, а добавление новых измерений
не имеет никакого эффекта. Фактически
категория ![]() при
при ![]() эквивалентна
категории
эквивалентна
категории ![]() ,
что является лишь примером того, как
действует так называемая «Периодическая
Таблица»
,
что является лишь примером того, как
действует так называемая «Периодическая
Таблица» ![]() -категорий
[13]. Часть её показана в таблице 3.
-категорий
[13]. Часть её показана в таблице 3.
|
|
|
|
|
|
|
множества |
категории |
2-категории |
|
|
моноиды |
моноидальные категории |
моноидальные 2-категории |
|
|
коммутативные моноиды |
сплетённые моноидальные категории |
сплетённые моноидальные 2-категории |
|
|
— " — |
симметричные моноидальные категории |
силлептические моноидальные 2-категории |
|
|
— " — |
— " — |
симметричные моноидальные 2-категории |
|
|
— " — |
— " — |
— " — |
|
|
— " — |
— " — |
— " — |
Таблица 3.
Периодическая Таблица: гипотетические
описания ![]() -категорий
в
терминах
-категорий
в
терминах ![]() -морфизмов
для
-морфизмов
для ![]()
В ![]() -категории
имеются не только морфизмы между
объектами, но и
-категории
имеются не только морфизмы между
объектами, но и
![]() -морфизмы
между морфизмами,
-морфизмы
между морфизмами, ![]() -морфизмы
между
-морфизмы
между ![]() -морфизмами
и т. д. до
-морфизмами
и т. д. до ![]() -морфизмов.
В топологии
-морфизмов.
В топологии ![]() -категории
используются для описания спутанных
поверхностей высших размерностей [14],
а в физике они могут применяться не
только для описания частиц, но и для
описания струн и мембран высших
размерностей [13, 15]. Представленный в
статье новый Розеттский камень относится
только к столбцу
-категории
используются для описания спутанных
поверхностей высших размерностей [14],
а в физике они могут применяться не
только для описания частиц, но и для
описания струн и мембран высших
размерностей [13, 15]. Представленный в
статье новый Розеттский камень относится
только к столбцу ![]() в
данной Периодической Таблице и является
фрагментом большего, всё ещё сокрытого
Розеттского камня для
в
данной Периодической Таблице и является
фрагментом большего, всё ещё сокрытого
Розеттского камня для
![]() -категорий.
-категорий.
2.6. Замкнутые категории
В квантовой механике линейный
оператор ![]() можно
перекодировать в квантовое состояние
с помощью техники, называемой «телепортация
через ворота» [47]. В топологии имеется
способ так прогнуть вход произвольного
тангла
можно
перекодировать в квантовое состояние
с помощью техники, называемой «телепортация
через ворота» [47]. В топологии имеется
способ так прогнуть вход произвольного
тангла ![]() ,
чтобы он стал частью выхода. В логике
можно преобразовать доказательство,
которое производится от предположения
,
чтобы он стал частью выхода. В логике
можно преобразовать доказательство,
которое производится от предположения ![]() к
заключению
к
заключению ![]() в
доказательство, без предположений
ведущее к заключению «из
в
доказательство, без предположений
ведущее к заключению «из ![]() следует
следует ![]() ».
В информатике можно рассматривать
программу, которая получает на вход
данные типа
».
В информатике можно рассматривать
программу, которая получает на вход
данные типа ![]() и
возвращает результат типа
и
возвращает результат типа ![]() ,
как значение нового «функционального
типа». Понятие, объединяющее данные
примеры, — «замкнутая категория».
,
как значение нового «функционального
типа». Понятие, объединяющее данные
примеры, — «замкнутая категория».
Для заданных объектов ![]() и
и ![]() в
категории
в
категории ![]() множество
морфизмов из
множество
морфизмов из ![]() в
в ![]() обозначается
как
обозначается
как ![]() .
В замкнутой категории также имеется
объект морфизмов из
.
В замкнутой категории также имеется
объект морфизмов из ![]() в
в ![]() ,
который обозначается как
,
который обозначается как ![]() (также
используются и другие способы
записи). В данном случае
(также
используются и другие способы
записи). В данном случае
![]() является
«внутренним
является
«внутренним
![]() -множеством»,
поскольку объект
-множеством»,
поскольку объект ![]() находится
внутри категории
находится
внутри категории ![]() ,
а не снаружи, как, например, в категории
множеств.
,
а не снаружи, как, например, в категории
множеств.
Замкнутые категории были введены в 1966
году С. Эйленбергом и Дж. М. Келли [39].
Хотя вышеупомянутые авторы могли
определить замкнутую структуру для
произвольной категории, выяснилось,
что внутреннее ![]() -множество
наиболее легко понять через моноидальные
категории. Причина в том, что рассматриваемая
категория при наличии тензорного
произведения, замкнута, если морфизмы
из
-множество
наиболее легко понять через моноидальные
категории. Причина в том, что рассматриваемая
категория при наличии тензорного
произведения, замкнута, если морфизмы
из
![]() в
в ![]() находятся
в естественном взаимно однозначном
соответствии с морфизмами из
находятся
в естественном взаимно однозначном
соответствии с морфизмами из ![]() в
в ![]() .
Другими словами, категория замкнута,
если существует естественный изоморфизм
.
Другими словами, категория замкнута,
если существует естественный изоморфизм ![]() ,
который переводит морфизм
,
который переводит морфизм ![]() в
в ![]() .
Например, в категории
.
Например, в категории ![]() при
при ![]() объектом
объектом ![]() является
множество функций из
является
множество функций из ![]() в
в ![]() ,
а потому имеется взаимно однозначное
соответствие между функциями
,
а потому имеется взаимно однозначное
соответствие между функциями ![]() ,
преобразующими элементы
,
преобразующими элементы ![]() в
в ![]() ,
и функциями
,
и функциями ![]() ,
которые получают на вход элементы
,
которые получают на вход элементы ![]() и
возвращают функции из
и
возвращают функции из ![]() в
в ![]() .
Такое соответствие выглядит следующим
образом:
.
Такое соответствие выглядит следующим
образом: ![]() .
.
Прежде чем рассматривать другие примеры,
стоит дать точное определение понятию
«замкнутая моноидальная категория».
Нужно иметь в виду, что для произвольной
категории ![]() имеется
функтор
имеется
функтор ![]() .
.
Определение 13. Двойственной
категорией ![]() категории
категории ![]() называется
категория, объекты которой тождественны
объектам из
называется
категория, объекты которой тождественны
объектам из ![]() ,
а морфизму
,
а морфизму ![]() соответствует
морфизм
соответствует
морфизм ![]() .
Композиция
.
Композиция ![]() соответствует
композиции
соответствует
композиции ![]() .
.
Определение 14. Для произвольной
категории ![]() функтор
функтор ![]() переводит
произвольный объект
переводит
произвольный объект ![]() в
множество
в
множество ![]() ,
а также переводит произвольный морфизм
,
а также переводит произвольный морфизм ![]() в
функцию
в
функцию ![]() ,
которая преобразует морфизм
,
которая преобразует морфизм ![]() в
композицию
в
композицию ![]() ,
в то время как
,
в то время как ![]() и
и ![]() —
морфизмы в
—
морфизмы в ![]() .
.
Определение 15. Моноидальная
категория ![]() называется
замкнутой слева, если существует
внутренний
называется
замкнутой слева, если существует
внутренний ![]() -функтор
-функтор ![]() и
естественный морфизм
и
естественный морфизм ![]() ,
называемый каррированием, который
ставит в соответствие произвольным
объектам
,
называемый каррированием, который
ставит в соответствие произвольным
объектам ![]() биекцию .
Та же категория называется замкнутой
справа, если в ней имеется такой же
внутренний
биекцию .
Та же категория называется замкнутой
справа, если в ней имеется такой же
внутренний ![]() -функтор
и естественный изоморфизм .
-функтор
и естественный изоморфизм .
Термин «каррирование» в основном
применяется в информатике, после
публикации работы Х. Б. Карри [35]. Далее
до конца данного раздела будет
предполагаться, что моноидальные
категории замкнуты справа. К счастью,
для перекрученных моноидальных категорий
нет большой разницы между левыми и
правыми замкнутыми категориями, поскольку
переключатель даёт изоморфизм ![]() .
.
Все рассматриваемые в настоящей статье
примеры моноидальных категорий являются
замкнутыми, но, как будет видно в
дальнейшем,
![]() вновь
стоит в стороне от остальных категорий:
вновь
стоит в стороне от остальных категорий:
-
Декартова категория
 замкнута,
при этом
замкнута,
при этом  является
множеством функций из
является
множеством функций из 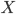 в
в 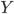 .
В категории
.
В категории  и в любой другой декартовой замкнутой
категории внутренний
и в любой другой декартовой замкнутой
категории внутренний
 -функтор
обычно обозначается как
-функтор
обычно обозначается как 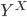 .
Чтобы уменьшить количество используемых
способов записи и подчёркнуть сходства
между различными случаями, далее вместо
.
Чтобы уменьшить количество используемых
способов записи и подчёркнуть сходства
между различными случаями, далее вместо
 всегда
будет использоваться запись
всегда
будет использоваться запись
 .
Для трактовки категории
.
Для трактовки категории
 как
замкнутой слева, необходимо
определить каррированную версию
морфизма
как
замкнутой слева, необходимо
определить каррированную версию
морфизма 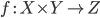 так
же, как это сделано ранее:
так
же, как это сделано ранее: 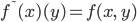 .
Для трактовки этой категории как
замкнутой справа вышеупомянутый
морфизм должен быть определён так:
.
Для трактовки этой категории как
замкнутой справа вышеупомянутый
морфизм должен быть определён так: 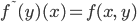 .
Подобные записи выглядят несколько
неудобными, но если изобразить морфизмы
в виде струнных диаграмм, всё станет
на свои места.
.
Подобные записи выглядят несколько
неудобными, но если изобразить морфизмы
в виде струнных диаграмм, всё станет
на свои места. -
Симметричная моноидальная категория
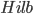 с
обычным тензорным произведением
является замкнутой, где
с
обычным тензорным произведением
является замкнутой, где  — множество линейных оператором
из
— множество линейных оператором
из 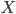 в
в  ,
используемых в гильбертовых пространствах
обычным образом. В этом случае можно
определить изоморфизм
,
используемых в гильбертовых пространствах
обычным образом. В этом случае можно
определить изоморфизм 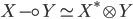 ,
где
,
где  —
пространство, двойственное (дуальное)
гильбертову пространству
—
пространство, двойственное (дуальное)
гильбертову пространству 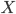 ,
так что множество линейных
операторов
,
так что множество линейных
операторов 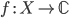 встроено
в гильбертово пространство обычным
способом.
встроено
в гильбертово пространство обычным
способом. -
Моноидальная категория
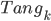 (при
(при 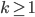 )
замкнута. Как и в категории
)
замкнута. Как и в категории 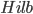 имеет
место
имеет
место 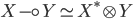 ,
где
,
где 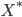 —
версия
—
версия 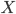 с
обращённой ориентацией.
с
обращённой ориентацией. -
Симметричная моноидальная категория
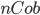 также
замкнута, при этом
также
замкнута, при этом 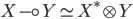 ,
где
,
где 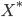 является
(
является
(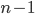 )-мерным
многообразием
)-мерным
многообразием  с
обращённой ориентацией.
с
обращённой ориентацией.
За исключением категории ![]() ,
все приведённые выше примеры фактически
являются «компактными» категориями.
По сути, это означает, что
,
все приведённые выше примеры фактически
являются «компактными» категориями.
По сути, это означает, что
![]() изоморфен
изоморфен ![]() ,
где
,
где ![]() —
некоторый объект, называемый «дуальным»
к
—
некоторый объект, называемый «дуальным»
к ![]() .
Чтобы придать определению большую
точность, необходимо определить понятие
«дуальности» для произвольной моноидальной
категории.
.
Чтобы придать определению большую
точность, необходимо определить понятие
«дуальности» для произвольной моноидальной
категории.
Для этого можно провести обобщение
случая для категории ![]() .
Как уже было упомянуто, каждый
объект
.
Как уже было упомянуто, каждый
объект ![]() имеет
дуальный объект
имеет
дуальный объект ![]() ,
состоящий из всех линейных операторов
,
состоящий из всех линейных операторов ![]() ,
где единичным объектом
,
где единичным объектом ![]() является
просто
является
просто ![]() .
Поэтому существует линейный оператор
.
Поэтому существует линейный оператор ![]() ,
переводящий
,
переводящий
![]() в
в ![]() ,
который называется коединицей
,
который называется коединицей ![]() .
Более того, пространство всех линейных
операторов из
.
Более того, пространство всех линейных
операторов из ![]() в
в ![]() может
быть идентифицировано с
может
быть идентифицировано с ![]() .
Так что также имеется линейный оператор,
называемый единицей
.
Так что также имеется линейный оператор,
называемый единицей ![]() :
: ![]() ,
который переводит произвольное
комплексное число
,
который переводит произвольное
комплексное число ![]() в
соответствующее произведение
тождественного оператора
в
соответствующее произведение
тождественного оператора ![]() .
.
Важность единицы и коединицы станет
более ясной, если рассмотреть некоторые
понятия по Р. Ф. Фейнману. В физике,
если ![]() является
гильбертовым пространством внутренних
состояний некоторой частицы, то
является
гильбертовым пространством внутренних
состояний некоторой частицы, то ![]() —
это гильбертово пространство состояний
соответствующей античастицы. Р. Ф.
Фейнман обнаружил, что понимание
античастиц в качестве частиц, двигающихся
назад во времени, крайне удобно. Поэтому
на диаграммах линии, помеченные как
—
это гильбертово пространство состояний
соответствующей античастицы. Р. Ф.
Фейнман обнаружил, что понимание
античастиц в качестве частиц, двигающихся
назад во времени, крайне удобно. Поэтому
на диаграммах линии, помеченные как ![]() ,
рисуются так же, как и линии для
,
рисуются так же, как и линии для ![]() ,
однако со стрелкой, направленной «назад
во времени», то есть вверх, а не вниз:
,
однако со стрелкой, направленной «назад
во времени», то есть вверх, а не вниз:

(Стоит отметить, что большинство
физиков расположило бы стрелки на
диаграммах в прямо противоположном
направлении — то есть вверх страницы
— однако, поскольку мы читаем снизу
вверх, то используется подход, в котором
время течёт сверху вниз).
Если
изображать ![]() как
как ![]() с
обращённым временем, то единицу можно
было бы изобразить в виде шляпки
(cap):
с
обращённым временем, то единицу можно
было бы изобразить в виде шляпки
(cap):
![]()
а коединицу в виде чашечки (cup):
![]()
В диаграммах Фейнмана данные изображения отражают создание и аннигиляцию виртуальных пар «частица-античастица»!
Как видно, единица и коединица удовлетворяют двум уравнениям, которые называются уравнениями зигзагов:
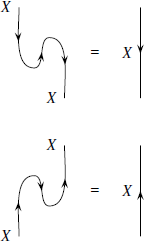
Проверка данных диаграмм — интересная задача в рамках линейной алгебры — предоставляется читателю. Если записать вышеприведённые уравнения в виде коммутативных диаграмм, то нужно включить в них некоторые ассоциаторы и образы единиц, отчего диаграммы выглядят несколько громоздкими:
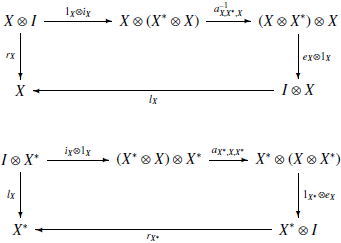
Но они в действительности показывают возможность выпрямления зигзагов на струнных диаграммах.
Наиболее показательны примеры с
категориями
![]() и
и ![]() .
Так, в категории
.
Так, в категории ![]() при
условии, что
при
условии, что ![]() представляет
собой круг, единица выглядит следующим
образом:
представляет
собой круг, единица выглядит следующим
образом:
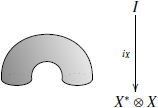
в то время как коединица выглядит так:
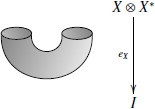
В даном случае, согласно уравнениям зигзагов, можно выпрямить изогнутые части труб. Теперь несколько определений.
Определение 16. Для заданных
объектов ![]() и
и ![]() в
моноидальной категории объект
в
моноидальной категории объект ![]() называется
дуальным справа к
называется
дуальным справа к ![]() ,
а объект
,
а объект ![]() называется
дуальным слева к
называется
дуальным слева к ![]() ,
если существуют морфизмы
,
если существуют морфизмы ![]() и
и ![]() ,
называемые единицей и коединицей
соответственно и удовлетворяющие
уравнениям зигзагов.
,
называемые единицей и коединицей
соответственно и удовлетворяющие
уравнениям зигзагов.
Можно показать, что левый и правый дуальные объекты уникальны (может, лучше "однозначно определяемы"?) с точностью до канонического изоморфизма. Так что обычно говорится о «конкретных» правых или левых дуальных объектов, если они существуют.
Определение 17. Моноидальная
категория ![]() называется
компактной, если для каждого
объекта
называется
компактной, если для каждого
объекта ![]() существуют
левый и правый дуальные объекты.
существуют
левый и правый дуальные объекты.
Часто вместо слова «компактный»
используется термин «автономный».
Многие авторы оставляют слово «компактный»
для случаев, когда категория ![]() является
симметричной или, по крайней мере,
сплетённой; тогда левые дуальные объекты
совпадают с правыми, упрощая картину
[42]. Ещё большую путаницу вносит тот
факт, что компактные симметричные
моноидальные категории часто просто
называются «компактными замкнутыми
категориями».
является
симметричной или, по крайней мере,
сплетённой; тогда левые дуальные объекты
совпадают с правыми, упрощая картину
[42]. Ещё большую путаницу вносит тот
факт, что компактные симметричные
моноидальные категории часто просто
называются «компактными замкнутыми
категориями».
Отчасти употребление последнего
термина объясняется тем, что произвольная
компактная моноидальная категория
автоматически является замкнутой!
Вначале определяется внутренний ![]() -функтор
над объектами как
-функтор
над объектами как ![]() .
Далее необходимо показать, что операция
.
Далее необходимо показать, что операция ![]() естественным образом расширяется до
функтора
естественным образом расширяется до
функтора ![]() ,
так что
,
так что ![]() действительно
является функтором. Наконец, необходимо
проверить, что существует естественный
изоморфизм
действительно
является функтором. Наконец, необходимо
проверить, что существует естественный
изоморфизм ![]() .
На
струнных диаграммах этот изоморфизм
принимает на вход произвольный морфизм
следующей формы:
.
На
струнных диаграммах этот изоморфизм
принимает на вход произвольный морфизм
следующей формы:
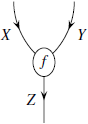
и преобразует входной канал, помеченный
символом ![]() ,
в выходной определённым образом:
,
в выходной определённым образом:
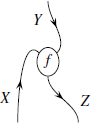
Теперь в компактной моноидальной категории имеет место:
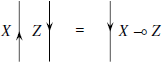
Но, как правило, замкнутые моноидальные
категории не позволяют стрелкам быть
направленными вверх! Поэтому изобразить
внутренний
![]() -функтор
для данных категорий — непростая задача.
Можно использовать ту же самую нотацию,
добавив в неё специальный элемент —
застёжку, — которая соединяет две
ленты вместе:
-функтор
для данных категорий — непростая задача.
Можно использовать ту же самую нотацию,
добавив в неё специальный элемент —
застёжку, — которая соединяет две
ленты вместе:
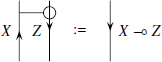
Только в случае, если рассматриваемая замкнутая моноидальная категория является компактной, можно обойтись без застёжки на диаграмме.
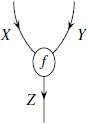
Пусть существует замкнутая моноидальная
категория. В этом случае морфизм ![]() изображается
как:
изображается
как:
Его каррированную версию ![]() можно изобразить с помощью переноса
входной линии, помеченной как
можно изобразить с помощью переноса
входной линии, помеченной как ![]() ,
таким образом, чтобы она стала частью
выхода:
,
таким образом, чтобы она стала частью
выхода:
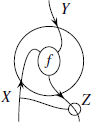
Необходимо отметить, что в том месте, где происходит закручивание входной линии, образуется «шляпка», похожая на следующую:
![]()
У замкнутых моноидальных категорий
на самом деле отсутствуют подобные
«шляпки», если только они не являются
компактными. Так что на диаграмме
необходимо изображать «пузырёк»,
в котором заключён морфизм ![]() ,
а также «застёжку» во избежание
недопустимых действий. Если рассматривается
компактная категория, то и «пузырёк»,
и застёжка могут опускаться, так что
морфизм
,
а также «застёжку» во избежание
недопустимых действий. Если рассматривается
компактная категория, то и «пузырёк»,
и застёжка могут опускаться, так что
морфизм ![]() изображается следующим образом:
изображается следующим образом:
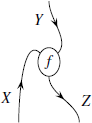
Особый случай каррирования даёт
идентификатор для
морфизма ![]() —
— ![]() ,
что достигается каррированием морфизма
,
что достигается каррированием морфизма ![]() .
С помощью струнных диаграмм морфизм
.
С помощью струнных диаграмм морфизм ![]() изображается следующим образом:
изображается следующим образом:
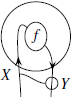
В категории ![]() единичным
объектом является одноэлементное
множество, синглетон
единичным
объектом является одноэлементное
множество, синглетон ![]() .
Таким образом, морфизм из этого объекта
во множество
.
Таким образом, морфизм из этого объекта
во множество ![]() различает
один элемент данного множества. В
частности, идентификатор
различает
один элемент данного множества. В
частности, идентификатор
![]() различает
один элемент множества
различает
один элемент множества ![]() ,
которое соответствует функции
,
которое соответствует функции ![]() .
Если обобщить, то в произвольной
декартовой замкнутой категории единичным
объектом является финальный объект
.
Если обобщить, то в произвольной
декартовой замкнутой категории единичным
объектом является финальный объект ![]() ,
а морфизм из финального объекта в
некоторый объект
,
а морфизм из финального объекта в
некоторый объект ![]() называется
точкой объекта
называется
точкой объекта ![]() .
Так что даже в этом случае можно говорить,
что идентификатором морфизма
.
Так что даже в этом случае можно говорить,
что идентификатором морфизма ![]() является точка объекта
является точка объекта ![]() .
.
Похожее правило действует и для
категории ![]() ,
хотя она является компактной, а не
декартовой. В категории
,
хотя она является компактной, а не
декартовой. В категории ![]() единичным
объектом
единичным
объектом
![]() является
просто
является
просто ![]() .
Так что ненулевой морфизм из
.
Так что ненулевой морфизм из ![]() в
произвольное гильбертово
пространство
в
произвольное гильбертово
пространство ![]() различает
ненулевой вектор в
различает
ненулевой вектор в ![]() ,
который может быть нормализован для
того, чтобы получить состояние в
,
который может быть нормализован для
того, чтобы получить состояние в ![]() :
поэтому подобный вектор называется
единичным. В частности, идентификатор
ненулевого морфизма
:
поэтому подобный вектор называется
единичным. В частности, идентификатор
ненулевого морфизма ![]() даёт
состояние
даёт
состояние ![]() .
Этот метод включения операторов в
состояния является основой «телепортации
сквозь ворота» [47].
.
Этот метод включения операторов в
состояния является основой «телепортации
сквозь ворота» [47].
Каррирование является биекцией, так
что можно построить обратную операцию
— декаррирование: ,
которая переводит заданный морфизм ![]() в
в ![]() .
.
Поскольку морфизм ![]() изображается
следующим образом:
изображается
следующим образом:
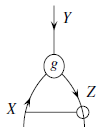
Декаррированная версия этого
морфизма ![]() изображается
путём прогиба выхода
изображается
путём прогиба выхода ![]() таким
образом, чтобы он стал входом:
таким
образом, чтобы он стал входом:
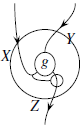
В случае, если не рассматривается
компактная моноидальная категория,
вновь необходимо изобразить «пузырёк»
вокруг «чашечки», когда производится
перепривязка линии, помеченной как ![]() Так
в оригинале. Предполагается, что
правильный является
Так
в оригинале. Предполагается, что
правильный является ![]() —
прим. перев. ,
—
прим. перев. ,
Хорошим примером операции декаррирования
является вычисляющий
морфизм: ![]() ,
который получается при декаррировании
тождественного морфизма:
,
который получается при декаррировании
тождественного морфизма: ![]() .
.
В
категории ![]() морфизм
морфизм ![]() получает
на вход функцию из
получает
на вход функцию из ![]() в
в ![]() и
вычисляет её для произвольного элемента
и
вычисляет её для произвольного элемента ![]() ,
получая на выходе элемент
,
получая на выходе элемент ![]() .
С помощью струнных диаграмм вычисляющий
морфизм изображается так:
.
С помощью струнных диаграмм вычисляющий
морфизм изображается так:

В произвольной замкнутой моноидальной категории можно лишить морфизм его идентификатора при помощи вычисления. Другими словами, следующая диаграмма коммутативна:
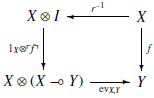
Или, применяя струнные диаграммы:
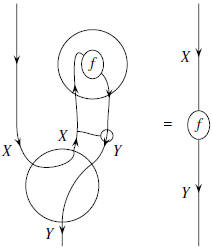
Доказательство предоставляется читателю. В большинстве случаев необходимо использовать каррирование. В случае с компактной моноидальной категорией есть наглядное доказательство. Нужно всего лишь удалить с диаграммы «пузырьки» и застёжку:

Результат следует из уравнений зигзага.
В предисловии к разделу, где речь шла о струнных диаграммах, не было указано, как данные диаграммы применяются для решения конкретных задач. Поэтому сейчас авторы предлагают некоторый материал для дальнейшего изучения:
-
Представления групп Ли играют большую роль в квантовой физике, особенно в калибровочной теории поля. Каждая группа Ли обладает компактной симметричной моноидальной категорией конечноразмерных представлений. В своей книге «Теория групп» П. Цвитанович [36] разработал детальное описание струнных диаграмм для данных категорий представлений, взяв классические группы Ли
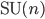 и
и 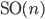 и
некоторые особые «исключительные»
группы Ли. Его книга также иллюстрирует,
как облегчить сложные вычисления в
калибровочной теории поля.
и
некоторые особые «исключительные»
группы Ли. Его книга также иллюстрирует,
как облегчить сложные вычисления в
калибровочной теории поля. -
Квантовые группы являются обобщением групп, которые проявляются в двух- и трёхмерной физике. Их отличительной чертой является наличие сплетённой моноидальной категории своих представлений. Книга Л. Х. Кауффмана «Узлы и физика» [59] даёт отличное представление того, как квантовые группы проявляют себя в теории узлов и физике, а термин «струнные диаграммы» встречается в ней на каждом шагу. Более подробно квантовые группы и сплетённые моноидальные категории описаны в книге К. Касселя [58].
-
Л. Х. Кауффман и С. Линс [60] с помощью струнных диаграмм прекрасно описали категорию представлений для простейшей квантовой группы
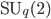 .
Они также использовали данное описание
для конструирования некоторых известных
инвариантов трёхмерных многообразий,
ассоциированных с
трёх- и четырёхмерными теориями
квантового поля: инвариантов
Уиттена-Решетихина-Тураева, Тураева-Виро
и Крейна-Йеттера. В работе Л. Х. Кауффмана
и С. Линса струнные диаграммы часто
называются «
.
Они также использовали данное описание
для конструирования некоторых известных
инвариантов трёхмерных многообразий,
ассоциированных с
трёх- и четырёхмерными теориями
квантового поля: инвариантов
Уиттена-Решетихина-Тураева, Тураева-Виро
и Крейна-Йеттера. В работе Л. Х. Кауффмана
и С. Линса струнные диаграммы часто
называются «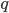 -деформированными
сплетёнными сетями» [91]. Для изучения
общих характеристик других квантовых
групп можно обратиться к работам В. Г.
Тураева [97] или Б. Бакалова и А. Кириллова
[16]. Ключевой составляющей является
особый вид компактных сплетённых
категорий, называемый «модульными
тензорными категориями».
-деформированными
сплетёнными сетями» [91]. Для изучения
общих характеристик других квантовых
групп можно обратиться к работам В. Г.
Тураева [97] или Б. Бакалова и А. Кириллова
[16]. Ключевой составляющей является
особый вид компактных сплетённых
категорий, называемый «модульными
тензорными категориями». -
Дж. Кок [64] написал отличное введение в двухмерные топологические квантовые теории поля, использующие для работы с категорией
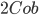 метод
диаграмм.
метод
диаграмм. -
С. Абрамский, Б. Кёке и их соавторы [2, 3, 4, 30, 32, 33] разработали струнные диаграммы как способ для понимания квантовых вычислений. Книга Б. Кёке «Квантовая механика: проще простого» [31] — наиболее подходящий вариант для ознакомления с данной темой.
2.7. Обращающие
категории
Исследование, проводимое
авторами, было бы неполным без подробного
рассмотрения гибльбертовых пространств
и применения к ним скалярного произведения,
то есть того, что составляет суть
квантовой теории.
Всё, что ранее
было сказано о категории ![]() ,
в равной степени применимо и к категории
,
в равной степени применимо и к категории ![]() ,
то есть категории конечномерных векторных
пространств и линейных операторов.
Обе категории являются компактными
симметричными моноидальными категориями
и в некотором смысле эквивалентны.
[72].
Чем же так особенна категория
,
то есть категории конечномерных векторных
пространств и линейных операторов.
Обе категории являются компактными
симметричными моноидальными категориями
и в некотором смысле эквивалентны.
[72].
Чем же так особенна категория ![]() ?
В теории категорий можно взять гильбертово
пространство, сопряжённое с произвольным
линейным оператором
?
В теории категорий можно взять гильбертово
пространство, сопряжённое с произвольным
линейным оператором ![]() между
конечномерными гильбертовыми
пространствами, и получить, тем самым,
оператор
между
конечномерными гильбертовыми
пространствами, и получить, тем самым,
оператор ![]() .
Подобная способность «обращать» морфизмы
даёт повод назвать категорию
.
Подобная способность «обращать» морфизмы
даёт повод назвать категорию ![]() «обращающей»:
«обращающей»:
Определение 18. Обращающей
категорией является такая категория ![]() ,
в которой для каждого морфизма
,
в которой для каждого морфизма ![]() существует
определённый морфизм
существует
определённый морфизм ![]() такой,
что
такой,
что ![]() для
произвольной пары морфизмов, к которой
применима операция композиции, а
также
для
произвольной пары морфизмов, к которой
применима операция композиции, а
также ![]() для
произвольного морфизма.
для
произвольного морфизма.
Аналогично, обращающая категория связана
с функтором ![]() ,
который тождественен для объектов и
удовлетворяет правилу
,
который тождественен для объектов и
удовлетворяет правилу ![]() для
любого морфизма.
для
любого морфизма.
Фактически, все рассматриваемые
примеры категорий можно преобразовать
в обращающие, за исключением категории ![]() :
:
-
Категория
 не
может быть обращающей, поскольку в ней
существует функция, получающая пустое
множество на входе и синглетон на
выходе, а правила обращения для подобной
функции отсутствуют.
не
может быть обращающей, поскольку в ней
существует функция, получающая пустое
множество на входе и синглетон на
выходе, а правила обращения для подобной
функции отсутствуют. -
Категория
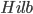 становится
обращающей следующим образом. Для
заданного морфизма
становится
обращающей следующим образом. Для
заданного морфизма 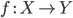 имеется
морфизм
имеется
морфизм 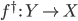 ,
то есть сопряжённое гильбертово
пространство к
,
то есть сопряжённое гильбертово
пространство к 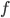 ,
который определяется как
,
который определяется как 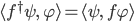 для
произвольных
для
произвольных 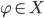 и
и 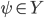 .
. -
Для произвольного
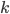 категория
категория 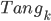 становится
обращающей, если морфизм
становится
обращающей, если морфизм
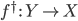 получается
при помощи отражения морфизма
получается
при помощи отражения морфизма 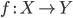 по
вертикали, после чего производится
обращение маленьких стрелок, обозначающих
направление дуг и кривых.
по
вертикали, после чего производится
обращение маленьких стрелок, обозначающих
направление дуг и кривых. -
Для произвольного
 категория
категория 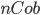 становится
обращающей, если морфизм
становится
обращающей, если морфизм 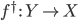 получается
при помощи перестановки входа и выхода
морфизма
получается
при помощи перестановки входа и выхода
морфизма 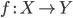 и
обращения направлений всех соединённых
элементов
и
обращения направлений всех соединённых
элементов  .
Для наглядности:
.
Для наглядности:
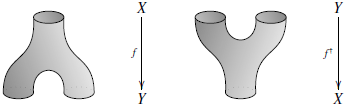
Применимо к физике операция обращения «переставляет будущее и прошлое местами».
Во всех вышеперечисленных примерах
категории прекрасно сочетают обращающие
свойства со свойствами моноидальных
категорий, а также c переключателем,
если он существует. Можно составить
перечень постулатов, описывающих данное
взаимодействие [2, 3, 87]. Как видно,
возможность «обращения» морфизмов —
ещё одно отличие «квантовых» категорий
от категории множеств и функций. Данный
вывод имеет большое значение как для
основ квантовой теории [11], так и для
топологической теории квантовых полей
[13], где обращающие категории — пример
«![]() -категорий
с двойниками» [14]. Последние еще только
предстоит основательно изученить.
3.
Логика
-категорий
с двойниками» [14]. Последние еще только
предстоит основательно изученить.
3.
Логика
