
- •1. Теорема Фробениуса-Перрона. Определение числа и вектора Фробениуса неотрицательной матрицы.
- •3. Докажите следующее утверждение. Пусть s и s – минимальная и максимальная суммы элементов столбцов матрицы а. Тогда число Фробениуса λА матрицы а удовлетворяет неравенству s
- •5. Сформулируйте и докажите первый критерий продуктивности
- •6. Докажите, что если неотрицательная квадратная матрица продуктивна, то ее число Фробениуса меньше 1
- •7. Сформулируйте определение запаса продуктивности неотрицательной матрицы. Выведите формулу для вычисления запаса продуктивности через число Фробениуса.
- •9. Приведите примеры задач лп на минимум (задача о диете) и на максимум (задача об использовании ресурсов)
- •10. Приведите общую постановку злп. Дайте определения следующим терминам: целевая ф-ия, допустимое мн-во задачи, оптимальное решение, оптимальное мн-во.
- •26.Приведите пример двух взаимно двойственных задач лп. Сформулируйте правило построения двойственной задачи.
- •27. Сформулируйте и докажите основное неравенство для взаимно двойственных задач лп. Сформулируйте достаточный признак оптимальности.
- •28. Сформулируйте первую и вторую теоремы двойственности. Докажите вторую теорему двойственности (теорему равновесия)
- •29. Приведите пример постановки транспортной задачи. Что такое оптимальный план перевозок? Что такое транспортная задача с правильным балансом? Сформулируйте критерий разрешимости транспортной задачи.
- •30. Опишите методы построения начального опорного плана транспортной задачи (метод северо-западного угла, метод минимального тарифа.
- •38. Опишите модель Самуэльсона-Хикса. Какие экономические предположения лежат в ее основе? Запишите уравнение Хикса. В каком случае решением уравнения Хикса является стационарная последовательность?
- •39. Опишите паутинную модель рынка. Какие экономические предположения лежат в ее основе? Найдите равновесное состояние паутинной модели рынка.
30. Опишите методы построения начального опорного плана транспортной задачи (метод северо-западного угла, метод минимального тарифа.
Начальным опорным планом называется план перевозок X=(xij), который удовлетворяет всем ограничениям транспортной задачи. Начальный опорный план находят, заполняя не более чем m+n-1 клеток (по числу базисных переменных). Любое допустимое решение транспортной задачи можно записать в транспортную таблицу. Клетки транспортной таблицы, в которых находятся отличные от нуля (или базисные ненулевые) перевозки, называются занятыми, остальные — свободными. Клетки таблицы нумеруются так, что клетка, содержащая перевозку xij , т. е. стоящая в i-ой строке и j-ом столбце, имеет номер (i,j).
При нахождении опорного плана транспортной задачи методом северо-западного угла на каждом шаге рассматривают первый из оставшихся пунктов отправления и первый из оставшихся пунктов назначения. Заполнение клеток таблицы условий начинается с левой верхней клетки для неизвестного x11 (“северо-западный угол”) и заканчивается для неизвестного xmn, т. е. идет как бы по диагонали таблицы с севера на запад.
Согласно методу минимального тарифа, выбор заполняемых клеток производят, ориентируясь на тарифы перевозок, а именно: на каждом шаге выбирают какую-нибудь клетку (i,j), равную минимальному тарифу и помещают в нее максимально возможную перевозку xij . После этого обнуляют либо столбец, либо строку в зависимости от соотношения xij=b или xij=a.
31.Опишите метод потенциалов. Сформулируйте определения следующих понятий: свободная клетка, занятая клетка, оценка свободной клетки, цикл, перестановка по циклу. В чем состоит условие оптимальности опорного плана?
Метод потенциалов используется для оценки плана. Он основан на следующей теореме: Если допустимое решение X=(xij)(i= (1;m);j= (1;n)) транспортной задачи является оптимальным, то существуют потенциалы поставщиков u1(i= (1;m)) и потребителей
v1(j= (1;n)) , удовлетворяющие условиям: u1+ v1 = cij, если xij>0, u1+ v1 ≤ cij, если xij=0.
Равенства u1+ v1 = cij, при xij>0, используются для нахождения потенциалов. Данная система уравнений имеет m+n неизвестных. Число уравнений системы, как и число отличных от нуля координат невырожденного опорного решения, равно m+n-1. Так как число неизвестных системы на единицу больше числа уравнений, то одно из них можно задать произвольно (как правило, его берут нулевым), а остальные найти из системы.
Неравенства u1+ v1 ≤ cij, при xij=0 используются для проверки оптимальности опорного решения. Эти неравенства удобно записать в виде ∆ij = u1+ v1 - cij, при xij=0.
Числа ∆ij называются оценками свободных клеток таблицы, не входящих в базис опорного решения. В этом случае признак оптимальности можно сформулировать так же как в симплекс-методе (в задаче на минимум): опорное решение является оптимальным, если для всех клеток таблицы оценки неположительные.
Если же ∆ij >0, то для соответствующей клетки строят цикл и улучшают решение, перераспределяя груз t=min (xij) по этому циклу. Сдвигом по циклу на величину t называется увеличение объемов перевозок во всех нечетных клетках цикла, отмеченных знаком «+», на t и уменьшение объемов перевозок во всех четных клетках, отмеченных знаком «-», на t.
Свободная клетка – клетка в которой нет перевозки. Занятая клетка – клетка, в которой есть перевозки.
Циклом называется такая последовательность клеток таблицы транспортной задачи (i1, j1), (i1, j2 ), (i2 , j2 ),…,(ik , j1 ) , в которой две и только две соседние клетки расположены в одной строке или столбце, причем первая и последняя клетки также находятся в одной строке или столбце.
32.Сформулируйте определение разностного уравнения порядка k и его общего решения. Сформулируйте определение линейного разностного уравнения порядка k с постоянными коэффициентами. Сформулируйте теоремы об общем решении однородного и неоднородного уравнения (без доказательства).
Уравнение вида F(n;xn;xn+1;...;xn+k)=0, где k-фиксированное, а n-произвольные натуральные числа, xn;xn+1;...;xn+k — члены некоторой неизвестной числовой последовательности, называется разностным уравнением порядка k.
Общим решением разностного уравнения k-го порядка называется его решение
xn=φ(n; C1; C2;...;Ck), зависящее от k независимых произвольных постоянных C1; C2;...;Ck. Количество k постоянных равно порядку разностного уравнения, а независимость означает, что ни одно из постоянных нельзя выразить через другие.
Линейным разностным уравнением k-ого порядка с постоянными коэффициентами называется уравнение вида:
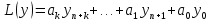 ,
где ai
– постоянные коэффициенты (
,
где ai
– постоянные коэффициенты (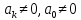 ).
).
Теорема об общем решении линейного неоднородного уравнения.
Общее решение линейного неоднородного
разностного уравнения
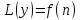 есть сумма частного решения
есть сумма частного решения
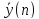 этого уравнения и общего решения
соответствующего ему однородного
уравнения.
этого уравнения и общего решения
соответствующего ему однородного
уравнения.
Теорема об общем решении линейного однородного уравнения.
Пусть
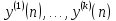 - система, состоящая из k
линейно независимых решений линейного
однородного разностного уравнения,
тогда общее решение этого уравнения
задается формулой:
- система, состоящая из k
линейно независимых решений линейного
однородного разностного уравнения,
тогда общее решение этого уравнения
задается формулой:
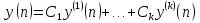 .
.
33. Опишите алгоритм решения однородного линейного разностного уравнения с постоянными коэффициентами. Сформулируйте определения следующих понятий: ФНР линейного разностного уравнения, характеристическое уравнение, определитель Казорати.
Множество решений линейного однородного
разностного уравнения k-ого
порядка образует k-мерное
линейное пространство, а любой набор
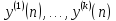 из k линейно независимых
решений (называемый фундаментальным
набором) является его базисом. Признаком
линейной независимости решений
из k линейно независимых
решений (называемый фундаментальным
набором) является его базисом. Признаком
линейной независимости решений
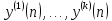 однородного уравнения является
неравенство нулю определителя
Казоратти:
однородного уравнения является
неравенство нулю определителя
Казоратти:
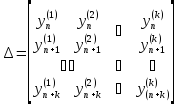
Уравнение
 называется характеристическим уравнением
однородного линейного уравнения. Знание
корней характеристического уравнения
позволяет построить общее решение
однородного разностного уравнения.
Рассмотрим это на примере уравнения
второго порядка:
называется характеристическим уравнением
однородного линейного уравнения. Знание
корней характеристического уравнения
позволяет построить общее решение
однородного разностного уравнения.
Рассмотрим это на примере уравнения
второго порядка:
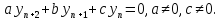 Полученные в результате решения могут
быть без труда перенесены на случай
уравнений более высокого порядка.
Полученные в результате решения могут
быть без труда перенесены на случай
уравнений более высокого порядка.
В зависимости от значений дискриминанта
D=b2-4ac
характеристического уравнения
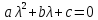 возможны следующие случаи:
возможны следующие случаи:
-
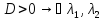 – корни х. уравнения, тогда общее решение
уравнения имеет вид
– корни х. уравнения, тогда общее решение
уравнения имеет вид
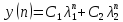 ;
; -
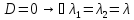 - корень х. уравнения, тогда общее решения
уравнения имеет вид
- корень х. уравнения, тогда общее решения
уравнения имеет вид
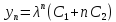 ;
; -
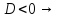 корни комплексные
корни комплексные
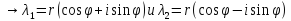 ,
где r – модуль λ1,
а
,
где r – модуль λ1,
а
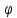 - его аргумент. Общее решение уравнения
имеет вид
- его аргумент. Общее решение уравнения
имеет вид
 .
.
C1,C2 – произвольные постоянные.
Для нахождения частного решения неоднородного линейного разностного уравнения используется метод неопределенных коэффициентов, основанный на подборе частного решения неоднородного уравнения по виду правой части f(n).
34-37. В каком виде нужно искать частное решение разностного уравнения.
