[Править] Примеры

Наглядными примерами евклидовых пространств могут служить пространства:

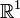• размерности 1 (вещественная прямая)

• размерности 2 (евклидова плоскость)

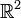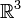• размерности 3 (евклидово трехмерное пространство)

• Евклидово пространство можно считать современной интерпретацией и обобщением (так как оно допускает размерности больше трех) классической (Евклидовой) геометрии.

Можно привести и несколько более абстрактные примеры:

• пространство вещественных многочленов степени, не превосходящей n, со скалярным произведением, определенным как интеграл произведения по конечному отрезку (или по всей прямой, но с быстро спадающей весовой функцией)

• вообще пространство всех линейных комбинаций конечного набора вещественных функций

• пространство состояний конечномерной квантовой системы (или конечномерное подпространство полного пространства состояний) в вещественном представлении.

Ортогональные матрицы.

Ортогональная матрица — квадратная матрица A с вещественными элементами, результат умножения которой на A^T равен единичной матрице:^[1]

AA^T = A^TA = E,

или, что эквивалентно, её обратная матрица равна транспонированной матрице:

Свойства

• Столбцы и строки ортогональной матрицы образуют системы ортонормированных векторов, то есть:

и

где , n — порядок матрицы, а δ_jk — символ Кронекера.

Другими словами, скалярное произведение строки на саму себя равно 1, а на любую другую строку — 0. Так же и для столбцов.

• Определитель ортогональной матрицы равен 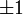, что следует из свойств определителей:

• Множество ортогональных матриц порядка n над полем k образует группу по умножению, так называемую ортогональную группу которая обозначается O_n(k) или 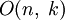(если k опускается, то предполагается ).

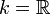• Ортогональные матрицы соответствуют линейным операторам, переводящим ортонормированный базис линейного пространства в ортонормированный.

• Любая вещественная ортогональная матрица подобна блочно-диагональной матрице с блоками вида

и

[Править] Примеры

• — единичная матрица

• 

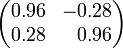• — пример матрицы поворота

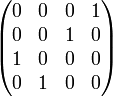• — пример перестановочной матрицы

Канонический вид квадратичной формы

  Квадратичная форма называется канонической, если все т. е.

     Всякую квадратичную форму можно привести к каноническому виду с помощью линейных преобразований. На практике обычно применяют следующие способы.

     1. Ортогональное преобразование пространства :

где - собственные значения матрицы A.

     2. Метод Лагранжа - последовательное выделение полных квадратов. Например, если

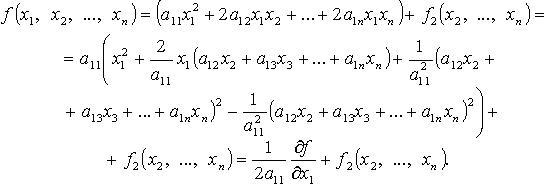
Затем подобную процедуру проделывают с квадратичной формой и т. д. Если в квадратичной форме все но есть то после предварительного преобразования дело сводится к рассмотренной процедуре. Так, если, например, то полагаем

     3. Метод Якоби (в случае, когда все главные миноры квадратичной формы отличны от нуля):

 Нормальный вид квадратичной формы

     Для действительной квадратичной формы

где r = rank A.

     Для комплексной квадратичной формы

    r = rank A.

     Для действительных квадратичных форм имеет место закон инерции квадратичных форм: число положительных и число отрицательных квадратов в нормальном виде квадратичной формы не зависит от способа приведения квадратичной формы к нормальному виду с помощью невырожденных линейных преобразований.

Основные понятия ТВ: событие, полная группа, равновозможные события.

Теоремы сложения и умножения вероятностей

теорема сложения вероятностей:вероятность проявления одного(безразлично какого) события из нескольких несовместимых событий равна сумме их вероятностей.(несовместимые-события, которые не могут произойти одновременно).Вероятность осуществления одного из двух несовместимых событий А и Б: Р(Аили Б)=Р(А)+Р(Б) например:при бросании случайным образом кубика на гранях которого выгравированы цифры от 1 до 6, классическая вероятность выпадения одной конкретной цифры-1/6, а количество нечетных чисел- три. Какова при этом вероятность выпадения нечетной цифры? Р(1или3или5)=Р(1)+Р(3)+Р(5)=1/6+1/6+1/6=3/6=1/2 Теорема умножения вероятностей:вероятность совместного проявления независимых событий равна произведению их вероятностей. Вероятность двух событий будет: Р(А и Б)= Р(А) *Р(Б) К примеру,бросания кубика,какова вероятность того, что при следующих друг за другом бросках выпадут числа 1и 6? Р(1и 6)=Р(1)+Р(6)=1/6*1/6=1/36

Теоремы сложения: 1) пусть А и Б - два несовместных события, тогда вероятность их суммы равна сумме вероятностей слагаемых, т.е. Р(А+Б)=Р(А)+Р(Б) 2) пусть А и Б - два совместных события, тогда вероятность их суммы равна сумме вероятностей слагаемых без вероятности произведения, т.е. Р(А+Б)=Р(А)+Р(Б)-Р(АБ) Теоремы умножения: 3) пусть А и Б - два независимых события, тогда вероятность их произведения равна произведению вероятностей сомножителей, т.е. Р(АБ)=Р(А)Р(Б) 4) пусть А и Б - два зависимых события, тогда вероятность их произведения равна произведению вероятностей первого множителя на вероятность второго, вычисленную в предположении, что первое событие произошло (или вероятности второго множителя на вероятность первого, вычисленную в предположении, что второе событие произошло), т.е. Р(АБ)=Р(А)Р(Б/А)=Р(Б)Р(А/Б)

Законы больших чисел

Зако́н больши́х чи́сел в теории вероятностей утверждает, что эмпирическое среднее (среднее арифметическое) достаточно большой конечной выборки из фиксированного распределения близко к теоретическому среднему (математическому ожиданию) этого распределения. В зависимости от вида сходимости различают слабый закон больших чисел, когда имеет место сходимость по вероятности, и усиленный закон больших чисел, когда имеет место сходимость почти всюду.

Всегда найдётся такое количество испытаний, при котором с любой заданной наперёд вероятностью частота появления некоторого события будет сколь угодно мало отличаться от его вероятности. Общий смысл закона больших чисел — совместное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая.