Примеры

• Нулевое пространство, единственным элементом которого является ноль.

• Пространство всех функций 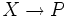с конечным носителем образует векторное пространство размерности равной мощности X.

• поле вещественных чисел может быть рассмотрено как континуально-мерное векторное пространство над полем рациональных чисел.

• Любое поле является одномерным пространством над собой.

Замена базиса. Матрица перехода. Преобразование координат.

Ма́трицей перехо́да от базиса к базису является матрица, столбцы которой — координаты разложения векторов в базисе .

Обозначается

Представление

Так как

.

.

.

.

Матрица перехода это

[править] Использование

При умножении столбца, составленного из коэффициентов разложения вектора по базису , на матрицу, обратную к матрице перехода, мы получаем тот же вектор, выраженный через базис .

Из-за того, что уменьшает объём работы при переводе векторов аффинных пространств и в пространстве столбцов Rⁿв другие базисы, используется в трёхмерном моделировании.

[править] Пример

Для того, чтобы повернуть вектор на угол θ против часовой стрелки, можно умножить матрицу поворота на него:

Свойства

• Матрица перехода является невырожденной. То есть определитель этой матрицы не равен нулю.

• 

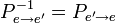
[править] Пример поиска матрицы

найдём матрицу перехода от базиса 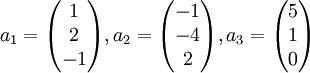к единичному базису путём элементарных преобразований

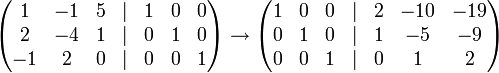следовательно

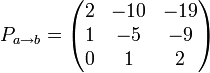
Пусть системы векторов e = {e₁, ..., e_n} и f = {f₁, ..., f_n} — два базиса n-мерного линейного пространства L_n.

Обозначим x_e = (x₁,x₂, ..., x_n) и x_f = (x'₁,x'₂, ..., x'_n) — координаты вектора x ∈ L_n соответственно в базисах e и f.

Справедливо следующее x_e= C_e→f·x_f :

Здесь C_e→f — матрица перехода от базиса e к базису f, это матрица, столбцами которой являются координаты базисных векторов f₁, ..., f_n  в базисе  e₁, ..., e_n:

f₁ = с₁₁· e₂ + с₂₁· e₁ + ... + с_n1· e_n, f₂ = с₁₂· e₁ + с₂₂· e₂ + ... + с_n2· e_n, ..., f_n = с_1n· e₂ + ... + с_nn· e_n.

Формулу преобразования координат вектора при изменении базиса принято записывать в виде

x_f= (C_e→f)^{− 1}·x_e

Ранг системы векторов и ранг матрицы

Рангом системы строк (столбцов) матрицы A с m строк и n столбцов называется максимальное число линейно независимых строк (столбцов). Несколько строк (столбцов) называются линейно независимыми, если ни одна из них не выражается линейно через другие. Ранг системы строк всегда равен рангу системы столбцов, и это число называется рангом матрицы.

Ранг матрицы — наивысший из порядков миноров этой матрицы, отличных от нуля.

Теоре́ма Кро́некера — Капе́лли — критерий совместности системы линейных алгебраических уравнений:

Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.

Доказательство (условия совместности системы)

[править] Необходимость

Пусть система совместна. Тогда существуют числа такие, что . Следовательно, столбец b является линейной комбинацией столбцов матрицы A. Из того, что ранг матрицы не изменится, если из системы его строк (столбцов) вычеркнуть или приписать строку (соответственно столбец), которая является линейной комбинацией других строк (соответственно столбцов) следует, что .

[править] Достаточность

Пусть . Возьмем в матрице A какой-нибудь базисный минор. Так как , то он же и будет базисным минором и матрицы B. Тогда согласно теореме о базисном миноре последний столбец матрицы B будет линейной комбинацией базисных столбцов, то есть столбцов матрицы A. Следовательно, столбец свободных членов системы является линейной комбинацией столбцов матрицы A.

[править] Следствия

• Количество главных переменных системы равно рангу системы.

• Совместная система будет определена (её решение единственно), если ранг системы равен числу всех её переменных.

Линейные преобразования: Определение и примеры

Рассмотрим линейное пространство и преобразование этого пространства, то есть закон, по которому каждому вектору из соответствует вектор из того же пространства. Вектор называется образом вектора и обозначается , а вектор называется прообразом вектора .

        Определение 19.1   Преобразование линейного пространства называется линейным, если для любых векторов и и любого числа выполнены равенства

(19.1)

то есть образ суммы векторов равен сумме образов слагаемых, образ вектора, умноженного на число, равен произведению этого числа на образ вектора.         

        Замечание 19.1   В этой главе с каждым линейным преобразованием будет связана матрица, которую мы будем обозначать той же буквой, что и само преобразование. Чтобы их различать, мы для букв, обозначающих преобразование, будем использовать так называемый "каллиграфический" шрифт.         

Линейное преобразование пространства называют также линейным отображением из в или линейным оператором из в .

Исходя из равенств (19.1) легко проверить, что

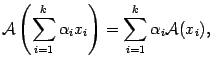
то есть образ линейной комбинации векторов равен линейной комбинации их образов.

Рассмотрим несколько примеров линейных преобразований.

        Пример 19.1   Пусть  -- двумерное векторное пространство, то есть множество векторов плоскости. Пусть . Это преобразование действует так: каждый вектор оно переводит в вектор такого же направления, но в два раза большей длины. Если считать, что все векторы имеют начало в начале координат, то преобразование можно представить как растяжение плоскости в два раза (рис. 19.1).

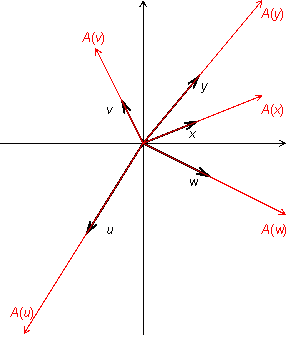
Рис.19.1.Преобразование растяжения

Проверим выполнение равенств (19.1)

Равенства (19.1) выполнены, следовательно, преобразование является линейным.         

        Пример 19.2   Пусть  -- двумерное векторное пространство,  -- поворот вектора по часовой стрелке на угол (рис. 19.2).

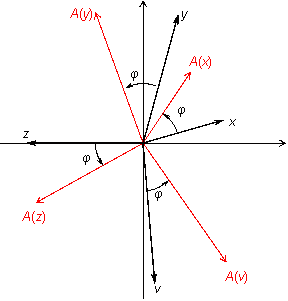
Рис.19.2.Преобразование поворота

Покажем, что это -- линейное преобразование.

Пусть и  -- два вектора. Тогда  -- это диагональ параллелограмма со стронами , (рис. 19.3).

Рис.19.3.Образ суммы векторов

Если параллелограмм повернуть как единое целое на угол , то его стороны станут векторами и , диагональ будет вектором . С другой стороны, диагональ тоже повернулась на угол и поэтому является вектором . Следовательно, , первое из условий (19.1) выполнено.

Пусть -- число. Из рисунка 19.4 очевидно, что .

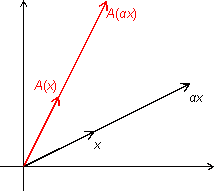
Рис.19.4.Образ вектора, умноженного на число

Следовательно, преобразование  -- линейное.         

 

Функции и их графики Всюду в тексте учебника мы будем использовать общепринятые обозначения, те, что используются и в школьных учебниках. В частности, означает числовую прямую (множество всех вещественных чисел); означает множество натуральных чисел ; означает множество всех целых чисел ;

Пределы Пусть задана некоторая меняющаяся величина , зависящая от переменного . Предположим, что это переменное можно менять так, что выполняется некоторое условие : переменное "приближается" ("стремится") к чему-нибудь (что это означает, мы уточним позже при помощи строгих определений). Тогда встаёт вопрос о том, не ведёт ли себя величина каким-либо "правильным" образом, тоже "стремясь" к чему-нибудь, например, к числу . Если это так, то это "что-то" называется пределом величины при данном условии для и обозначается

Линейное преобразование в разных базисах

В предыдущем разделе мы установили, что как только в линейном пространстве выбран базис, то каждому линейному преобразованию соответствует матрица этого преобразования. Однако если выбрать в пространстве другой базис, то матрица преобразования, как правило, станет другой. Выясним, как эти матрицы связаны между собой.

Пусть  -- -мерное линейное пространство, и  -- два базиса в этом пространстве. Первый из них назовем "старым", а второй -- "новым". Пусть  -- матрица перехода 19.1.4 а от старого базиса к новому.

        Предложение 19.1   Пусть  -- линейное преобразование пространства , и  -- матрицы этого преобразования в старом и новом базисе соответственно. Тогда

        Доказательство.     Пусть  -- произвольный вектор пространства ,  -- его образ, то есть . Пусть и  -- координатные столбцы векторов и в старом базисе, а ,  -- в новом. Тогда в силу формулы (19.3) . По  предложению 18.5 имеем , . Подставим эти выражения в предыдущую формулу, получаем . Откуда . С другой стороны, в силу формулы (19.3) в новом базисе . Сравнивая это равенство с предыдущим, получаем .     

        Определение 19.2   Две квадратных матрицы и одного порядка называются подобными, если существует такая невырожденная матрица , что .         

        Следствие 19.1   Матрицы одного линейного преобразования, соответствующие разным базисам, подобны друг другу, и наоборот, если матрицы подобны, то они являются матрицами одного и того же преобразования в разных базисах.

Собственные векторы и собственные значения

 Определение 19.3   Ненулевой вектор называется собственным вектором линейного преобразования , соответствующим собственному числу , если .

Совокупность всех собственных чисел линейного преобразования конечномерного линейного пространства называется спектром преобразования .         

Вместо слов "собственное число" говорят также собственное значение, характеристическое число или характеристическое значение.

Если  -- двумерное или трехмерное линейное пространство, то собственный вектор линейного преобразования -- это такой вектор, что его образ коллинеарен самому вектору. Иными словами, после применения преобразования (в вещественном случае) может измениться длина вектора, а направление или сохранится, или изменится на противоположное, или вектор станет равным нулю (в случае ).

В примере 19.1 любой вектор является собственным вектором линейного преобразования соответствующим собственному числу 2. В  примере 19.2 при не кратном преобразование не имеет собственных векторов, так как после применения преобразования длина каждого вектора не меняется и ни один вектор не сохраняет своего направления и не меняет направление на противоположное.

        Пример 19.7   Пусть  -- двумерное векторное пространство,  -- некоторая прямая, проходящая через начало координат,  -- преобразование, переводящее каждый вектор в вектор , симметричный исходному относительно прямой (рис. 19.5). Тогда из векторов рисунка 19.5 собственным вектором преобразования будет вектор , он соответствует собственному числу , и вектор , который соответствует собственному числу . Читатель без труда поймет, что любой ненулевой вектор, лежащий на прямой , будет собственным вектором, соответствующим собственному числу 1, а любой ненулевой вектор, лежащий на прямой перпендикулярной и проходящей через начало координат, является собственным вектором, соответствующим собственному числу .         

        Предложение 19.2   Пусть  -- собственный вектор линейного преобразования , соответствующий собственному числу и пусть  -- ненулевое число. Тогда  -- тоже собственный вектор линейного преобразования , соответствующий собственному числу .

        Доказательство.    

    

        Пример 19.8   Пусть  -- двумерное векторное пространство,  -- некоторая прямая, проходящая через начало координат,  -- преобразование, переводящее каждый вектор в его проекцию на прямую (рис. 19.6). Очевидно, что любой ненулевой вектор, лежащий на прямой , будет собственным вектором, соответствующим собственному числу 1, а любой ненулевой вектор на прямой перпендикулярной и проходящей через начало координат, будет собственным вектором, соответствующим собственному числу 0.         

        Пример 19.9   Пусть  -- линейное преобразование  примера 19.3. Очевидно, что векторы, являющиеся многочленами нулевой степени, то есть числами, будут собственными векторами, соотвествующими собственному числу 0.         

Если в пространстве задан базис, то линейному преобразованию соответствует матрица . Пусть  -- собственный вектор преобразования , соответствующий собственному числу ,  -- координатный столбец вектора . Тогда равенство означает, что .

        Определение 19.4   Ненулевая матрица-столбец называется собственным вектором квадратной матрицы , соответствующим собственному числу , если выполнено равенство .         

        Замечание 19.2   Между собственными числами (собственными векторами) матрицы и линейного преобразования есть некоторое различие. Линейное преобразование вещественного линейного пространства может не иметь собственных векторов и, соответственно, собственных чисел. Матрица же, как увидим дальше, всегда имеет хотя бы одно собственное число, быть может комплексное, и ему соответствует собственный вектор (тоже, быть может, комплексный). Но если рассматривать линейные преобразования -мерных комплексных пространств, то собственные числа преобразований совпадают с собственными числами матриц и собственные векторы преобразований имеют координатными столбцами собственные векторы матриц.         

        Предложение 19.3   Если две матрицы подобны, то наборы собственных чисел у них одинаковы.

        Доказательство.     Пусть и  -- две подобные матрицы порядка . Рассмотрим -мерное комплексное линейное пространство. Выберем в нем базис и рассмотрим линейное преобразование , которое в этом базисе имеет матрицу . По  следствию 19.1 будет матрицей того же преобразования в другом базисе. Так как собственные числа линейного преобразования не зависят от выбора базиса, то спектр (набор собственных чисел) преобразования будет совпадать со спектрами матриц и .

Существование и свойства собственных базисов

В разделе "Матрица линейного преобразования" мы выяснили, что каждое линейное преобразование -мерного линейного пространства в фиксированном базисе задается матрицей. Если меняется базис, то, как правило, меняется и матрица. Возникает вопрос, нельзя ли найти базис, в котором матрица линейного преобразования имеет наиболее простой вид. В общем случае выбрать такой базис довольно сложно. Это связано с нахождением нормальной жордановой формы матрицы, изложение которого можно найти в более обстоятельных учебниках по линейной алгебре, например, в [4], [5]. Следующая теорема отвечает на этот вопрос в более простом случае.

        Теорема 19.2   Пусть  -- линейное преобразование -мерного линейного пространства. Матрица линейного преобразования имеет диагональный вид

(19.5)

тогда и только тогда, когда векторы базиса являются собственнными векторами преобразования , соответствующими собственным числам .

        Доказательство.     Пусть преобразование имеет линейно независимых собственных векторов , соответствующих собственным числам . Так как векторы линейно независимы, то они образуют базис. Найдем матрицу преобразования в этом базисе. Ее первый столбец является координатным столбцом вектора . Так как  -- собственный вектор, то

Координатный столбец этого вектора . Второй столбец матрицы является координатным столбцом вектора . Так как  -- собственный вектор, то

Координатный столбец этого вектора 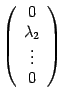. Вычисляя аналогично остальные столбцы, получаем, что матрица линейного преобразования в базисе имеет вид  (19.5). Первая часть теоремы доказана.

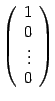Пусть в некотором базисе матрица линейного преобразования имеет вид (19.5). Найдем образ вектора . Этот вектор имеет координатный столбец , его образ имеет координатный столбец

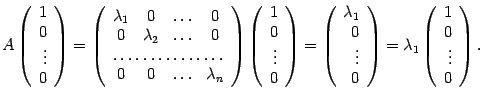
Следовательно,  -- собственное число преобразования , а  -- соответствущий ему собственный вектор. Аналогично находим, что любой базисный вектор является собственным вектором преобразования , соответствующим собственному числу .     

        Следствие 19.2   Если у матрицы порядка существует набор из линейно независимых собственнных векторов, соответствующих собственным числам , то матрица подобна диагональной матрице с числами на диагонали.

        Теорема 19.3   Пусть собственные векторы преобразования соответствуют собственным числам , среди которых нет равных друг другу. Тогда система векторов является линейно независимой.

        Доказательство.     Воспользуемся методом математической индукции по числу векторов. Если , то утверждение теоремы следует из того, что собственный вектор -- ненулевой.

Пусть утверждение верно для системы векторов . Составим линейную комбинацию векторов и приравняем ее к нулю

(19.6)

К обеим частям применим преобразование

По определению линейного преобразования получим

Так как  -- собственные векторы, то

Умножим равенство (19.6) на и вычтем из последнего равенства. Получим

Так как по предположению индукции векторы линейно независимы, то

По условию , следовательно, . Подставим эти значения в (19.6), получим . Получили, что из равенства (19.6) следует , то есть векторы линейно независимы.     

        Следствие 19.3   Если матрица порядка имеет попарно различных собственных чисел, то она подобна диагональной матрице.

Квадратичные формы и матрицы

Квадратичная форма — функция на векторном пространстве задаваемая однородным квадратным многочленом от координат.