[Править] Примеры

• В трёхмерном вещественном векторном пространстве векторов 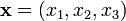введение скалярного произведения по формуле 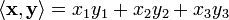превращает это пространство в евклидово пространство. Аналогичное утверждение верно для евклидова пространства любой размерности (в сумму тогда входит количество членов, равное размерности пространства).

  • В любом евклидовом пространстве (размерности n) всегда можно выбрать^[1] ортонормированный базис

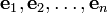
при разложении векторов по которому:

,

итд,

скалярное произведение будет выражаться приведенной выше формулой:

.

• В таком же, но комплексном, пространстве, скалярное произведение вводится по несколько другой формуле: 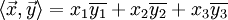. Здесь через 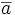обозначено число, комплексно сопряжённое к 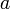. При таком определении скалярное произведение становится положительно определённым. Без комплексного сопряжения аксиома эрмитовости скалярного произведения была бы нарушена, а значит, вещественности определённой через него нормы вектора добиться бы не удалось, то есть норма в обычном смысле им бы не порождалась.

• В пространстве измеримых интегрируемых с квадратами на некоторой области Ω вещественных функций можно ввести положительно определённое скалярное произведение:

• В аналогичном случае для комплексных функций, если требуется эрмитовость (и положительная определённость) скалярного произведения, надо добавить комплексное сопряжение к f или g под интегралом.

• При использовании неортонормированных базисов скалярное произведение выражается через компоненты векторов с участием метрического тензора g_ij:

при этом сама метрика (говоря точнее, ее представление в данном базисе) так связана со скалярными произведениями базисных векторов :

• • (метрика в ортонормированных базисах тривиальна, то есть представлена единичной матрицей g_ij = δ_ij)

• Аналогичные конструкции скалярного произведения можно вводить и на бесконечномерных пространствах, например, на пространствах функций:

где К — положительно определённая, в первом случае симметричная относительно перестановки аргументов (при комплексных x — эрмитова) функция (если нужно иметь обычное симметричное положительно определённое скалярное произведение).

[Править] Неравенство Коши — Буняковского

Для любых элементов и линейного пространства со скалярным произведением выполняется неравенство [1]

[Править] Применение

Использование скалярного произведения крайне широко, как в элементарных, так и в весьма абстрактных областях математики, физики и прикладных наук.

Широко известны следующие применения:

• Любые геометрические вычисления (как собственно в математике, так и в приложениях), связанные с длинами, углами, проецированием, ортогональностью.

• Например, теорема косинусов легко выводится с использованием скалярного произведения:

• Угол между векторами:

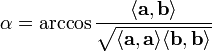
• Оценка угла между векторами:

в формуле знак определяется только косинусом угла (нормы векторов всегда положительны). Поэтому скалярное произведение > 0, если угол между векторами острый, и < 0, если угол между векторами тупой.

• Проекция вектора 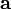на направление, определяемое единичным вектором :

,

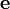• условие ортогональности^[2] (перпендикулярности) векторов 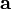и :

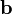итд.

(При этом технические возможности вычислений со скалярными произведениями, как и вообще с векторами, значительно возрастают, если использовать — при желании или необходимости — и компонентное представление векторов вкупе с компонентным выражением скалярного произведения).

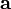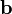• Площадь также выражается через скалярное произведение, например, двумерная площадь параллелограмма, натянутого на два вектора и , равна

• Аналогичные вычисления в геометризованных теориях в физике (таких, как СТО или ОТО).

• Разложение векторов по базису и переход к новому базису, являющееся основой многих разделов математики и ключевым приемом эффективного решения практических геометрических задач или практических задач, формулируемых на языке линейной алгебры (относящихся, например, к статистике).

• В том числе, в бесконечномерном случае: ряды Фурье, преобразования Фурье.

• В векторном анализе — вычисление контурных интегралов, потоков, применение с оператором набла.