Определения

Пусть L есть векторное пространство над полем K и — базис в L.

Функция Q из L в K называется квадратичной формой если её можно представить в виде

где , а a_ij элементы поля K.

[Править] Связанные определения

• Матрицу (a_ij) называют матрицей квадратичной формы в данном базисе.

  • В случае если характеристика поля K не равна 2, можно считать, что матрица квадратичной формы симметрична, то есть a_ij = a_ji.

• Для любой квадратичной формы Q существует единственная билинейная симметричная форма B, такая, что

Q(x) = B(x,x)

• Такую билинейную форму B называют полярной к Q.

• Полярная форма может быть вычислена по формуле

• Матрица квадратичной формы в произвольном базисе совпадает с матрицей полярной ей билинейной формы в том же базисе.

• Если матрица квадратичной формы имеет полный ранг, то квадратичную форму называют невырожденной, иначе — вырожденной.

• Квадратичная форма Q называется положительно (отрицательно) определённой, если для любого 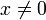Q(x) > 0 (Q(x) < 0).

  • Положительно определённые и отрицательно определённые формы называются знакоопределёнными.

  • Квадратичная форма A(x,x) называется знакопеременной, если она принимает как положительные, так и отрицательные значения.

  • Квадратичная форма Q называется полуопределенной, если .

[Править] Свойства

• Критерий Сильвестра

  • Квадратичная форма является положительно определенной, тогда и только тогда, когда все угловые миноры её матрицы строго положительны.

  • Квадратичная форма является отрицательно определенной, тогда и только тогда, когда знаки всех угловых миноров её матрицы чередуются, причем минор порядка 1 отрицателен.

• Билинейная форма, полярная положительно определённой квадратичной форме, удовлетворяет всем аксиомам скалярного произведения.

• Для любой квадратичной формы существует базис, в котором её матрица диагональна, а сама форма имеет канонический вид:

• Разность между числом положительных (p) и отрицательных (n − p) членов в этой записи называется сигнатурой квадратичной формы. Сигнатура, также как и числа положительных и отрицательных слагаемых, не зависят от способов приведения квадратичной формы к каноническому виду (закон инерции Сильвестра).

• Для приведения квадратичной формы к каноническому виду обычно используется метод Лагранжа.

[Править] Пример

Скалярное произведение векторов — симметричная билинейная функция. Соответствующая квадратичная функция сопоставляет вектору квадрат его длины.

Скалярное произведение. Евклидовы пространства.

Скаля́рное произведе́ние — операция над двумя векторами, результатом которой является скаляр (число), не зависящее от системы координат и характеризующее длины векторов-сомножителей и угол между ними. Данной операции соответствует умножение длины данного вектора x на проекцию другого вектора y на данный вектор x. Эта операция обычно рассматривается как коммутативная и линейная по каждому сомножителю.

Обычно используется одно из следующих обозначений:

,

,

,

или (обозначение Дирака, часто применяемое в квантовой механике для векторов состояния):

.

Обычно предполагается что скалярное произведение положительно определено, то есть

для всех .

Если этого не предполагать, то произведение называется индефинитным.