
- •Общий ход расчета методом перемещений
- •Учет односторонней связи с основанием
- •Общий алгоритм расчета
- •2. Решение
- •Прямоугольные плиты на упругом основании
- •Общие положения и составление системы разрешающих уравнений
- •8.4.2. Матрица жесткости прямоугольного элемента плиты
- •Матрица жесткости прямоугольного кэ плиты
- •Матрица жесткости прямоугольного кэ плиты
- •Матрица жесткости прямоугольного кэ плиты
- •Матрица жесткости прямоугольного кэ плиты
- •Матрица усилий прямоугольного кэ плиты
- •Учет односторонней связи с основанием
- •Матрица жесткости прямоугольного кэ плиты к примеру 8.4
- •Матрица жесткости прямоугольного кэ плиты к примеру 8.4
- •Матрица жесткости прямоугольного кэ плиты к примеру 8.4
- •Матрица погонных усилий Ng прямоугольного кэ плиты к примеру 8.4
8.4.2. Матрица жесткости прямоугольного элемента плиты
Для выражения поверхности прогиба примем бикубический полином, удовлетворяющий однородному дифференциальному уравнению изгибаемой плиты при отсутствии упругого основания:
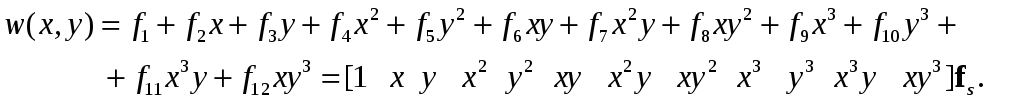 (8.66)
(8.66)
Полином (8.66) используется почти во всех работах, посвященных расчету тонких плит МКЭ. Это объясняется тем, что он дает достаточно точные результаты, особенно при решении задач прочности, хотя и допускает разрыв деформаций в углах поворота между смежными элементами.
Выражения для прогибов и углов поворота согласно (8.57) примут вид:
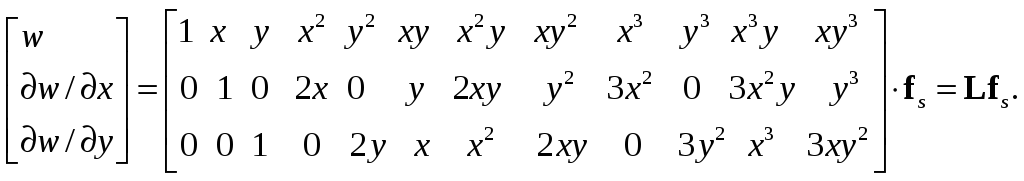 (8.67)
(8.67)
Подставив в матрицу L (8.67) координаты узлов конечного элемента (см. рис. 8.13), получим матрицу А коэффициентов при fs (8.3). Обращение этой матрицы дает A-1 (табл. 8.1):
Таблица 8.1
Матрица параметров fs для прямоугольного КЭ
|
A-1 |
= |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||
|
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||
|
–3/a2 |
–2/a |
0 |
3/a2 |
–1/a |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||
|
–3/b2 |
0 |
–2/b |
0 |
0 |
0 |
0 |
0 |
0 |
3/b2 |
0 |
–1/b |
||
|
–1/ab |
–1/b |
–1/a |
1/ab |
0 |
1/a |
–1/ab |
0 |
0 |
1/ab |
1/b |
0 |
||
|
3/a2b |
2/ab |
0 |
–3/a2b |
1/ab |
0 |
3/a2b |
–1/ab |
0 |
–3/a2b |
–2/ab |
0 |
||
|
3/ab2 |
0 |
2/ab |
–3/ab2 |
0 |
–2/ab |
3/ab2 |
0 |
–1/ab |
–3/ab2 |
0 |
1/ab |
||
|
2/a3 |
1/a2 |
0 |
–2/a3 |
1/a2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||
|
2/b3 |
0 |
1/b2 |
0 |
0 |
0 |
0 |
0 |
0 |
–2/b3 |
0 |
1/b2 |
||
|
–2/a3b |
–1/a2b |
0 |
2/a3b |
–1/a2b |
0 |
–2/a3b |
1/a2b |
0 |
2/a3b |
1/a2b |
0 |
||
|
–2/ab3 |
0 |
–1/ab2 |
2/ab3 |
0 |
1/ab2 |
–2/ab3 |
0 |
1/ab2 |
2/ab3 |
0 |
–1/ab2 |
Выражения для вторых производных от w получим из (8.67):
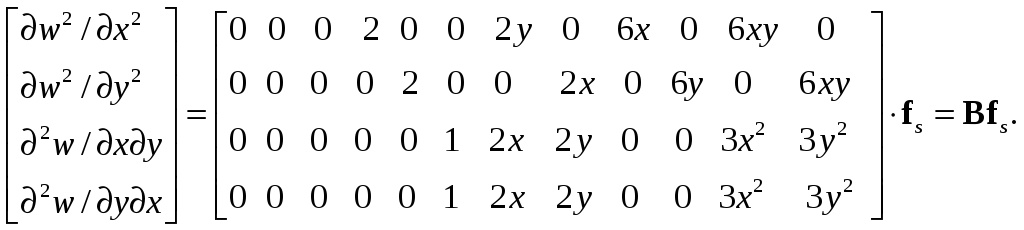 (8.68)
(8.68)
Матрица жесткости С (8.5) для бесконечного малого элемента в случае изгиба тонких ортотропных плит дает соотношения между изгибающими моментами и деформациями плиты:
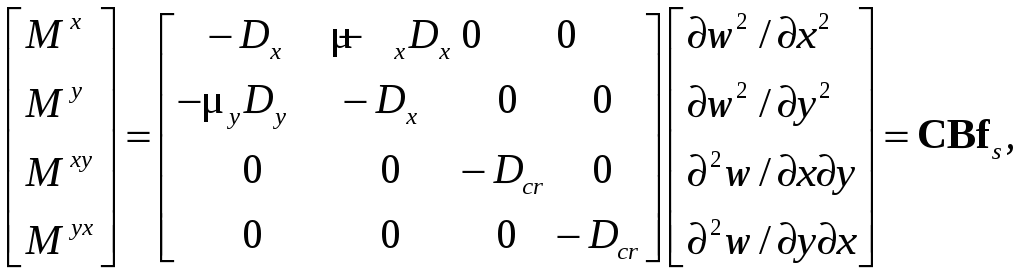 (8.69)
(8.69)
где Dx =Exh3/(12ν) – изгибная жесткость плиты в направлении оси x;
Dy =Eyh3/(12ν) – изгибная жесткость плиты в направлении оси y;
Dk =Gh3/6 – жесткость при кручении; μxDx = μyDy = Dμ; ν = 1– μx μy.
На основании принятой модели упругого основания [см. (8.32) и (8.33)] реакции упругого основания в матричной форме имеют вид:
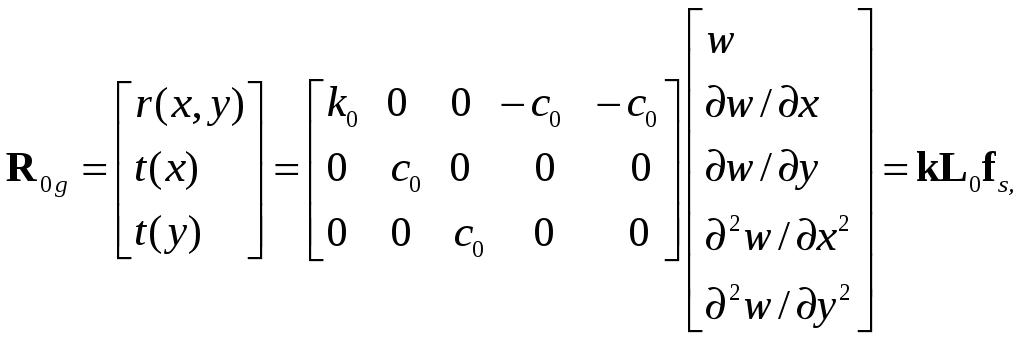 (8.70)
(8.70)
где
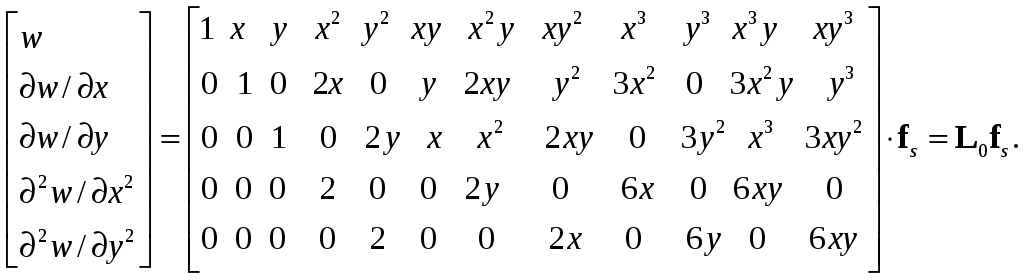 (8.71)
(8.71)
Подставляя матрицы
L
(8.67), A-1
(табл. 8.1), В
(8.68), С
(8.69), k
(8.70) и L0
(8.71) в выражения (8.19) и (8.20) и интегрируя
в пределах от 0 до а
в направлении оси x
и от 0 до b
в направлении оси y,
получим в общем виде:
![]() –матрицу
жесткости собственно конечного элемента,
учитывающую его упругие свойства;
–матрицу
жесткости собственно конечного элемента,
учитывающую его упругие свойства;
![]() –
матрицу, учитывающую свойства упругого
основания.
–
матрицу, учитывающую свойства упругого
основания.
Матрица
![]() представлена в виде суммы трех матриц:
представлена в виде суммы трех матриц:
![]() ,
где
,
где
![]() зависит от коэффициента k0,
а
зависит от коэффициента k0,
а
![]() и
и
![]() – от коэффициента с0
по направлениям
координатных осей. При
– от коэффициента с0
по направлениям
координатных осей. При
![]() =0
получаем наиболее распространенную и
простую модель упругого основании –
модель Винклера. При отсутствии упругого
основания
=0
получаем наиболее распространенную и
простую модель упругого основании –
модель Винклера. При отсутствии упругого
основания
![]() =
0. Матрицы жесткости
=
0. Матрицы жесткости
![]() ,
,
![]() ,
,
![]() и
и
![]() приведены,
соответственно, в таблицах 8.2, 8.3, 8.4 и
8.5.
приведены,
соответственно, в таблицах 8.2, 8.3, 8.4 и
8.5.
Распределенные
(погонные) усилия при расчете плиты
определяются по выражению (8.30), которое
в данном случае удобно записать в виде
![]() .
Матрица
.
Матрица
![]() приведена в таблице 8.6. В эту матрицу
подставляются координаты узлов для
изгибающих моментов и координаты
середины элемента – для крутящего
момента. Размер матрицы
приведена в таблице 8.6. В эту матрицу
подставляются координаты узлов для
изгибающих моментов и координаты
середины элемента – для крутящего
момента. Размер матрицы
![]() –
(9 х 12).
–
(9 х 12).
Таблица 8.2
