Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный архитектурно-строительный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Метод прогонки

.pdf

Скачиваний:

Добавлен:

29.03.2015

Размер:

437.24 Кб

Скачать

☆

Санкт-Петербургский государственный архитектурно-строительный университет

Кафедра Прикладной математики и информатики ст. преп. Ромаданова М.М.

Метод прогонки решения систем линейных алгебраических уравнений

с трехдиагональной матрицей

Рассмотрим систему линейных алгебраических уравнений с трехдиагональной матрицей

− C0 X0 + B0 X1		= F0
	A1 X0 − C1 X1 + B1 X2	= F1
	A1 X0 − C1 X1 + B1 X2	= F1
	A2 X1 − C2 X2 + B2 X3	= F2

	K	(1)
		(1)
	AI XI −1 − CI XI + BI XI +1	= FI

	K
	AN −1 XN −2 − CN −1 XN −1 + BN −1 XN = F N −1
		AN XN −1 − CN XN = F N
		AN XN −1 − CN XN = F N

Система может быть записана в матричном коэффициентов, X − вектор неизвестных, F

виде AX = F , где A − матрица − вектор правых частей

− C0

K K K

− C1

K K K

− C

A =

− C

− CN −1

K K K K 0 AN −1

0			X
				0
0			X1
0			X
				2

	, X =		K		,
0	, X =		XI		,
0			XI
			K

BN −1		XN −1
			XN
− CN			XN

	F0

	F1
	F 2
	F 2

F =	K	(2)
F =	FI	(2)
	FI

F N −1

F N

Будем искать решение системы уравнений (1) в виде

Xi	= αi Xi+1 + βi ,	(3)
где αi , βi − неизвестные пока прогоночные коэффициенты.
Положим в формуле (3) I = 0
X0	= α0 X1 + β0	(4)
и приведем первое уравнение системы (1)

− C0 X0 + B0 X1 = F0

к виду (3)

− C0 X0 = −B0 X1 + F0 ,

05 мая 2014г.

X0 = B0 X1 − F0 .

C0 C0

Откуда, с учетом (4), получаем начальные значения прогоночных коэффициентов

α0 =

, β0 = −

Рассмотрим теперь второе уравнение системы (1)

A1 X0 − C1 X1 + B1 X2 = F1 .

Исключим из него X0 , используя формулу (4)

A1 (α0 X1 + β0 ) − C1 X1 + B1 X2 = F1 ,

приведем к виду (3)

(α0 A1 − C1 ) X1 = −B1 X2 + ( F1 − β0 A1 ),

X1 =

X2 +

β0 A1 − F1

C1 − α0 A1

Сравнивая с выражением (3) при I =1 X1

= α1 X2

+ β1 , получим выражения для

коэффициентов α1 и β1

α1

C − α

β1

β0 A1 − F1

C1 − α0 A1

Исключим Xi−1 из I -го

уравнений

системы (1)

Ai Xi−1 − Ci Xi + Bi Xi+1 = Fi

с помощью формулы (3) Xi−1 = αi−1 Xi

+ βi−1

Ai Xi−1 − Ci Xi + Bi Xi+1 = Fi ,

Ai (αi−1 Xi + βi−1 )− Ci Xi + Bi Xi+1 = Fi ,

(αi−1 Ai − Ci ) Xi = −Bi Xi+1 + ( Fi − βi−1 Ai ) ,

Xi =

Xi+1 +

βi−1 Ai − Fi

Ci − αi−1 Ai

Сравнивая полученное выражение с

формулой (3) XI

= αI XI+1 + βI ,

получим

выражения для коэффициентов αi

и βI

αi

− α

i−1

βi

βi−1 Ai − Fi

− αi−1 Ai

Таким образом, мы получим все значения прогоночных коэффициентов

α0

β0 = −

(5.1)

αi =

βi

βi−1 Ai − Fi

I =1, 2,K, N .

Ci − αi−1 Ai

− αi−1 Ai

(5.2)

Процесс вычисления прогоночных коэффициентов по формулам (5.1)-(5.2) называется прямым ходом метода прогонки.

Ромаданова М.М.
Кафедра Прикладной математики и информатики СПбГАСУ	2

Запишем последнее уравнение системы (1) AN XN −1 − CN XN = FN и формулу

(3) при XN −1 = αN −1XN + βN −1

ANXN 1 − CNXN = FN ,

=− α + β

XN−1 N−1XN N−1

AN (αN −1XN + βN −1 ) − CN XN = FN ,

(αN −1 AN − CN ) XN = FN − βN −1 AN ,

XN = βN−1 AN − FN = βN .

CN − αN−1 AN

Далее используя формулу (3), получаем

XN = βN
XN−1 = α N−1 XN + βN−1
	= α N−2 XN−1	+ βN−2
XN−2
		(6)
K

X0 = α	0 X1 + β0

Процесс вычисления неизвестных по формулам (6) называется обратным ходом метода прогонки.

Таким образом, для решения системы уравнений (1) нужно циклом по формулам (5) найти прогоночные коэффициенты αi , βI . Последнее значение βN есть искомое значение XN . Остальные неизвестные находятся в обратном порядке по формулам (6).

Метод прогонки сходится, если выполнено условие Ai + Bi ≤ Ci ,

I =1, 2,K, N −1 .

Пример.

Найти решение системы линейных алгебраических уравнений с трехдиагональной матрицей

− X0 + X1						= −2
	− 2X1	− 2X2				= 5
X0	− 2X1	− 2X2				= 5
		− X2 + X3				= −4
	2X1	− X2 + X3				= −4
		5X2 − 3X3		− X4		= 6
		5X2 − 3X3		− X4		= 6

		X	3	+ X	4	= −3
			3		4

Запишем матрицу коэффициентов системы A и вектор правых частей F

	−1 1		0	0	0			− 2
		− 2 − 2 0
	1	− 2 − 2 0			0		5
	= 0		−1 1		0	,	F =	− 4 .
A	= 0	2	−1 1		0	,	F =	− 4 .

	0	0	5	− 3	−1		6

	0	0	0	1	1			− 3

Ромаданова М.М.
Кафедра Прикладной математики и информатики СПбГАСУ	3

Прямой ход метода прогонки 1) A0 =0 , C0 =1, B0 =1, F0 = −2

α0

=1,

β0

= −

− 2

= 2

2) A1 =1, C1 = 2 , B1 = −2 , F1 =5

α1

− 2

= −2

C1 − α0 A1

2 −1 1

β1

β0 A1 − F1

2 1− 5

= −3

C1 − α0 A1

2 −1 1

3) A2 =2 , C2 =1, B2 =1, F2 = −4

α2

= 0,2

C2 − α1 A2

(− 2)

1−

2 5

β2

β1 A2 − F2

(− 3) 2 − (− 4)

− 2

= −0,4

C2 − α1 A2

1− (− 2) 2

4) A3 = 5 , C3 = 3, B3 = −1, F3 = 6

−1

α3

= −0,5

C3 − α2 A3

3 − 0,2 5

β3

β2 A3 − F3

(− 0,4) 5 − 6

− 8

= −4

C3 − α2 A3

3 − 0,2 5

5) A4 =1, C4 = −1, B4 =0 , F4 = −3

α4

= 0

− α

β4

β3 A4 − F4

(− 4) 1− (− 3)

−1

= 2

C4 − α3 A4

−1− (− 0,5) 1 − 0,5

Обратный ход метода прогонки

X4 = β4 = 2

X3 = α3 X4 + β3 = −0,5 2 − 4 = −5

X2 = α2 X3 + β2 = 0,2 (− 5)− 0,4 = −1,4

X1 = α1 X2 + β1 = −2 (−1,4)− 3 = −0,2

X0 = α0 X1 + β0 =1 (− 0,2)+ 2 = 1,8

Ответ:

1,8

− 0,2

X= −1,4

− 5

Ромаданова М.М.
Кафедра Прикладной математики и информатики СПбГАСУ	4

Проверка.

Подставив полученные значения X в исходную систему уравнений, получим

−1	1	0	0	0	1,8		−1,8 − 0,2	− 2

1	− 2	− 2	0	0	− 0,2	1,8 − 2 (− 0,2)− 2 (−1,4)			5
0	2	−1	1	0	−1,4	=	2 (− 0,2)− (−1,4)− 5	=	− 4

0	0	5	− 3	−1	− 5		5 (−1,4)− 3 (− 5)− 2		6
							− 5 + 2		− 3
0	0	0	1	1	2		− 5 + 2		− 3

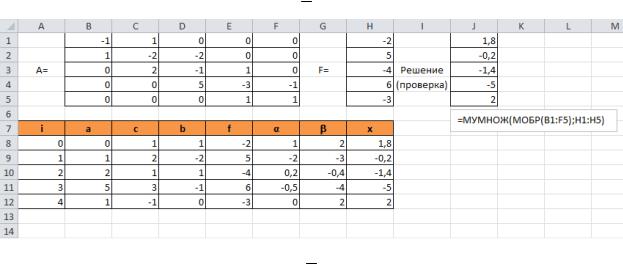
Реализация метода прогонки в MS Excel.

Пусть дана система уравнений AX = F с трехдиагональной матрицей.

Решение:

1.Запишем матрицу коэффициентов A в ячейки B1:F5 и вектор правых частей F в ячейки H1:H5.

2.Записываем коэффициенты системы Ai , Ci , Bi , стоящие на диагоналях, в столбики:

коэффициенты Ai − в ячейки B8:B12;

коэффициенты Ci − в ячейки C8:C12, причем коэффициенты Ci записываются с противоположным знаком;

коэффициенты Bi − в ячейки D8:D12.

3.Вектор правых частей F записываем в столбик E8:E12.

4.Выполняем прямой ход метода прогонки:

в ячейках F8 и G8 вычисляем начальные значения прогоночных

коэффициентов по формулам α0	=	B0	, β0	= −	F0	;

		C0			C0

в ячейки F9 и G9 записываем выражения для коэффициентов α1 и β1 , согласно формулам (5.2), и протягиваем их вниз до ячеек F12 и G12.

5.Выполняем обратный ход метода прогонки:

начинаем с последнего значения X4 = β4 (ячейка H12=G12);

в ячейку H11 записываем формулу X3 = α3 X4 + β3 и протягиваем вверх до

ячейки H8. Таким образом, в ячейках H8:H12 мы получили решение системы уравнений.

6.Для проверки в ячейках J1:J5 найдено решение с помощью обратной матрицы: =МУМНОЖ(МОБР(B1:F5); H1:H5).

Ромаданова М.М.
Кафедра Прикладной математики и информатики СПбГАСУ	5

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
29.03.2015517.63 Кб38Мет.пос. по ВКР-ГАСУ-2010.doc
#
11.07.2019403.46 Кб4Мет_задачи1.doc
#
29.03.2015834.83 Кб29Металлы и сплавы.pdf
#
29.03.201519.17 Mб19МЕТАЛЛЫ.pdf
#
27.10.20185.14 Mб19МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ.doc
#
29.03.2015437.24 Кб26Метод прогонки.pdf
#
07.05.2019223.23 Кб4Метод рек-и по написанию курсовых работ.doc
#
28.03.20154.25 Mб95Метод. Сопромат1.doc
#
28.03.20153.78 Mб98Метод. Сопромат2.doc
#
26.09.201927.68 Mб68Метод.реком. по выпол. к.р. по НГИГ + к.р..doc
#
29.03.20153.15 Mб4методdocs_205.pdf