Учет односторонней связи с основанием

КЭ с четырьмя степенями свободы

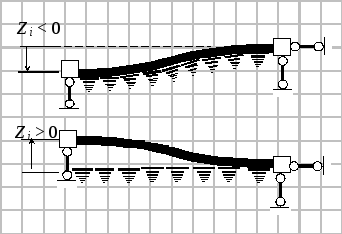
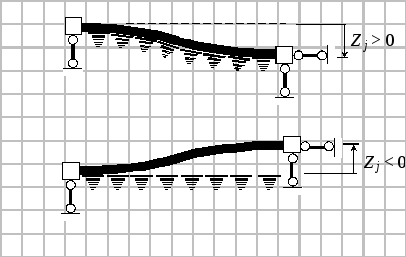
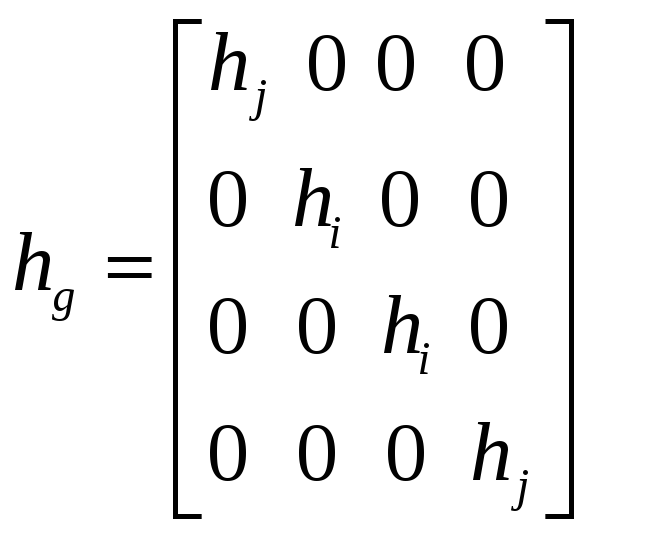(51)

КЭ с тремя степенями свободы

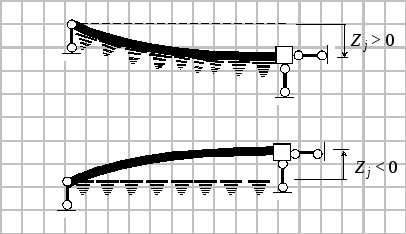
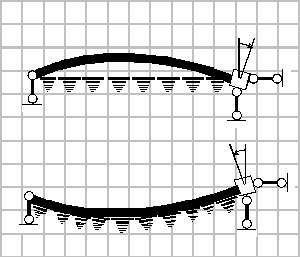
(52)

Общий алгоритм расчета

• без учета односторонней связи

(53)

• с учетом односторонней связи

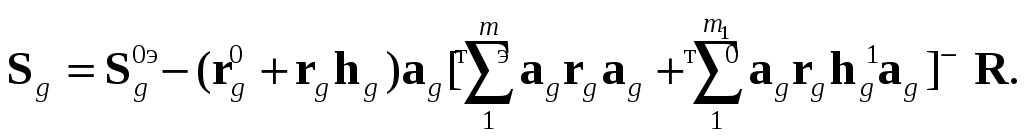(54)

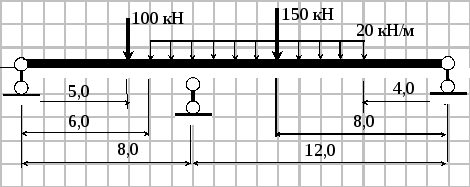
Пример 1.

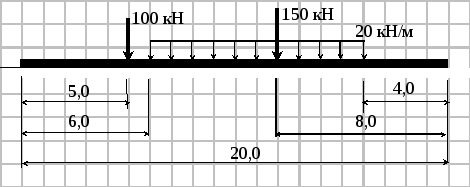
k₀ = 32000 кН/м³; b = 1,25 м; EI = 2,56∙10⁶ кН∙м²

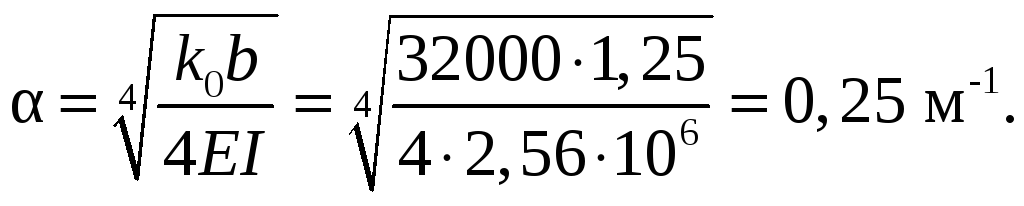
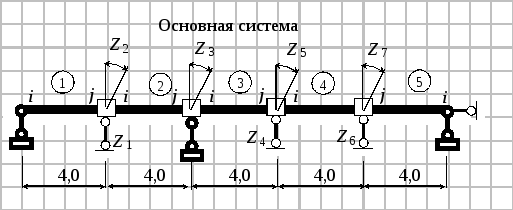
Принимаем длину конечных элементов l=4,0 м. Тогда величина αl = 0,25∙4 = 1

1. Исходные матрицы

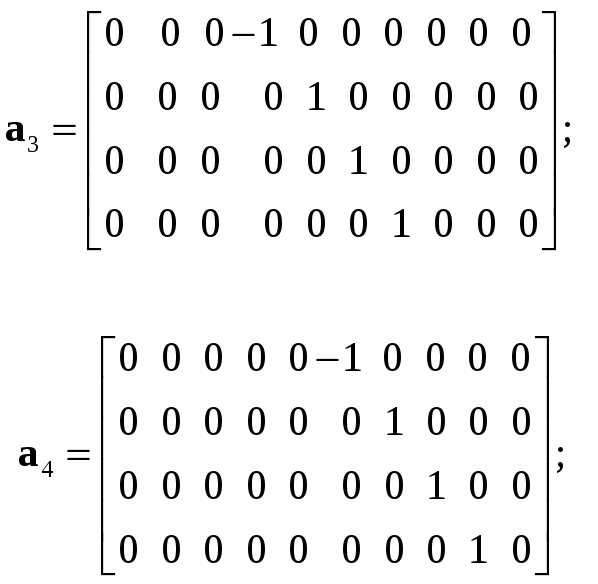
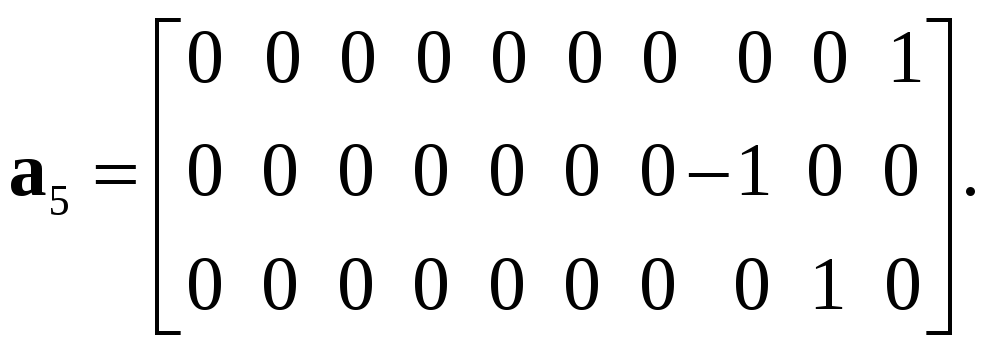
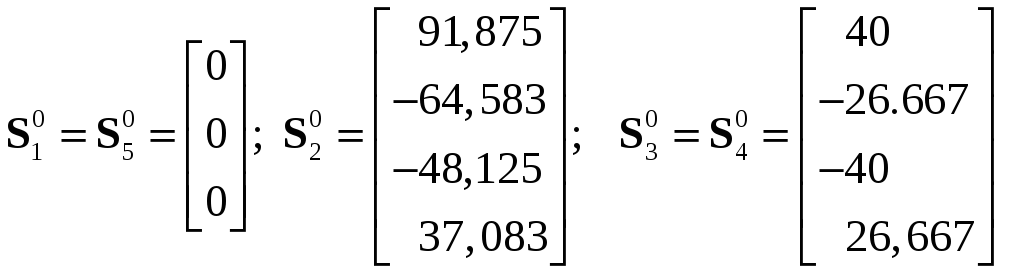
2. Решение

3. Определим усилия в сечении k второго КЭ в точке приложения силы F =100 кН .

Реакция упругого основания

r(x) = k₀∙b∙w = 19,172 +5,38x– 0,486x² + 0,028x³.

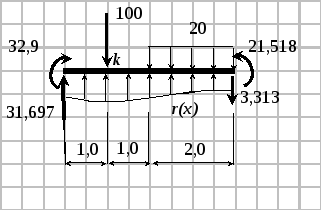
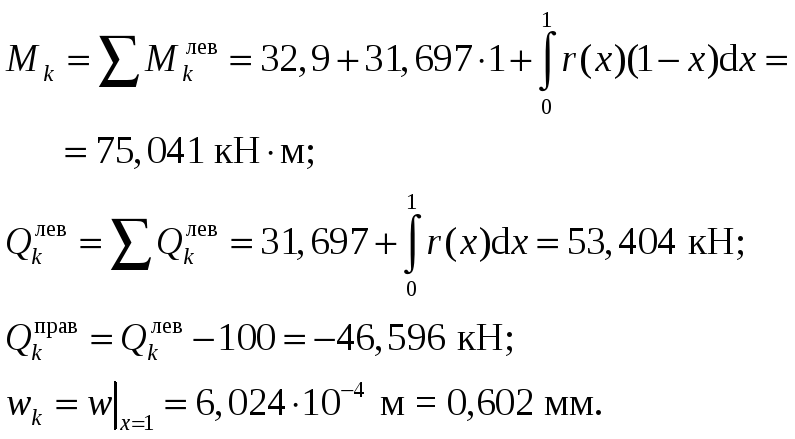
4. Учет односторонней связи балки с упругим основанием.

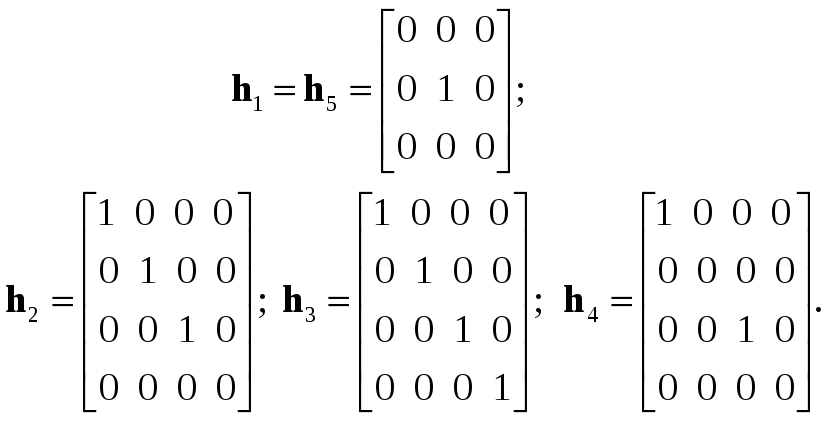
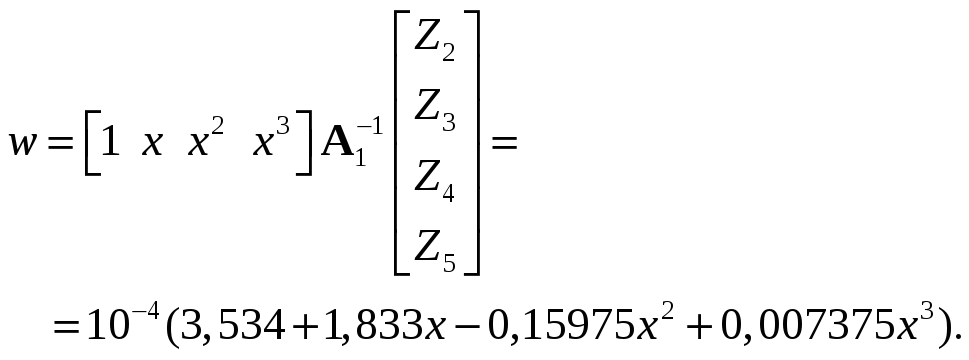
r(x) = k₀∙b∙w = 14,136 +7,332– 0,639x² + 0,0295x³.

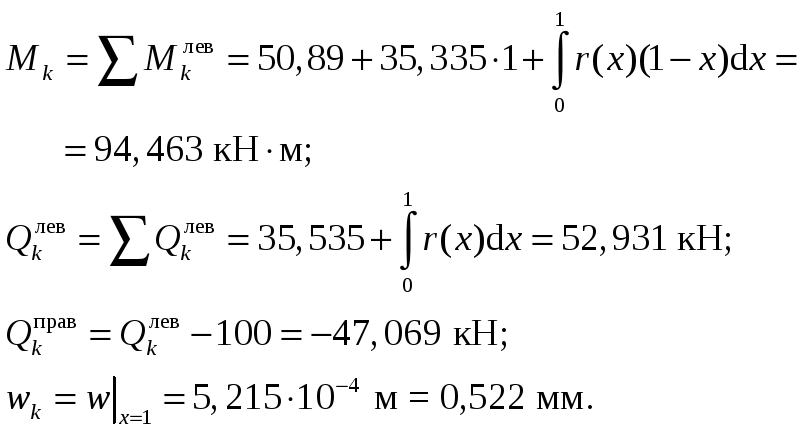
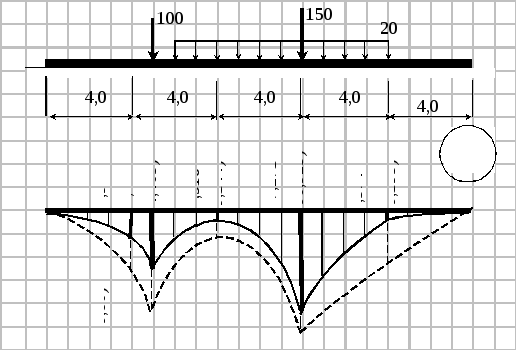
Преобразованные матрицы жесткости

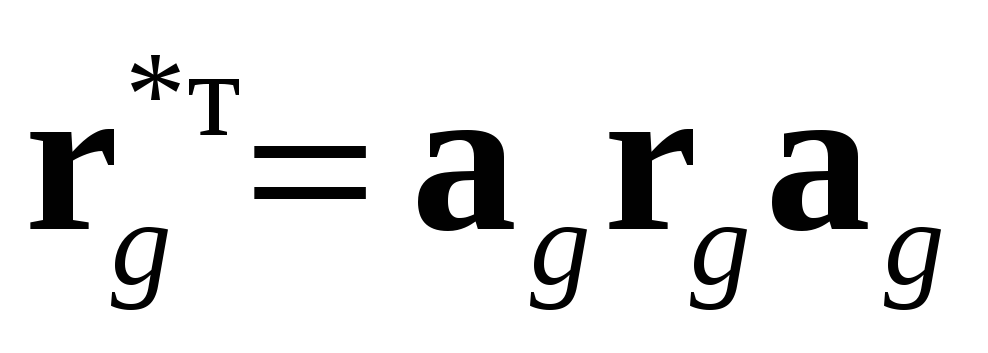
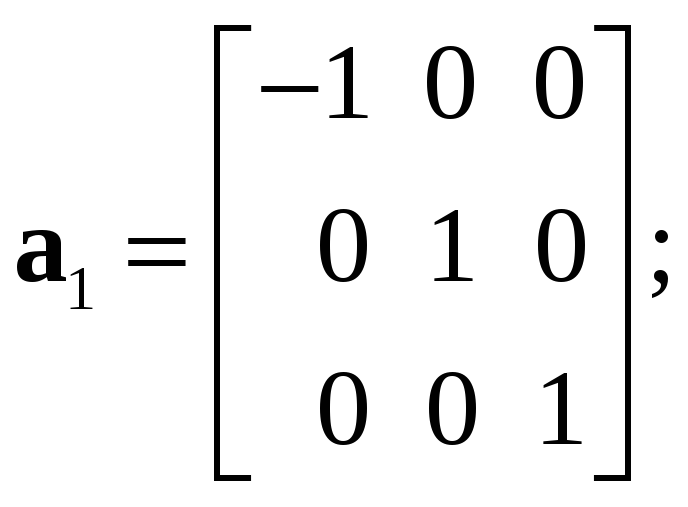
Пример 2.

k₀ = 26000 кН/м³; b = 1,0 м; EI = 0,2∙10⁶ кН∙м².

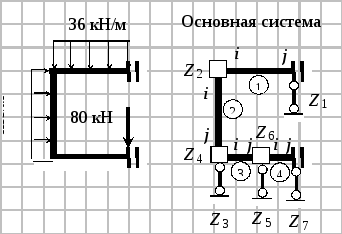
Принимаем размер КЭ l = 2,0 м.

Тогда величина αl = 0,42∙2 = 0,84 находится в допустимых пределах

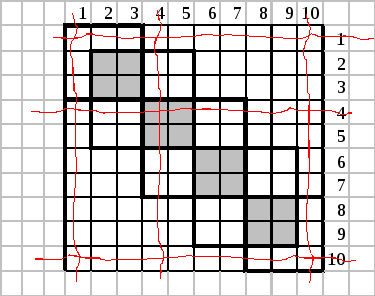
1. Исходные матрицы.

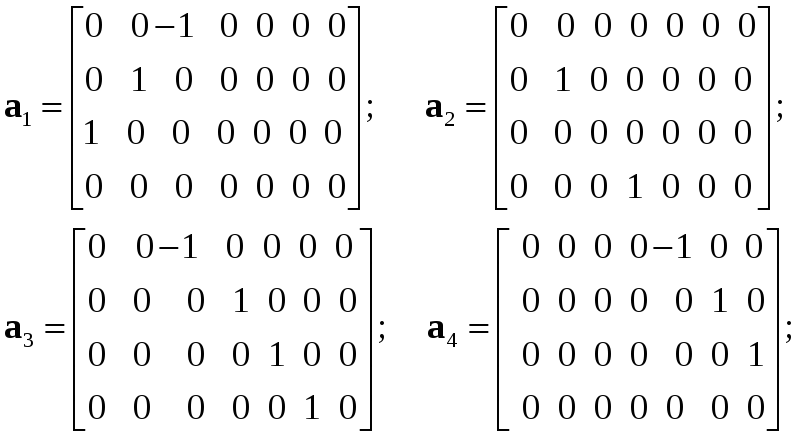
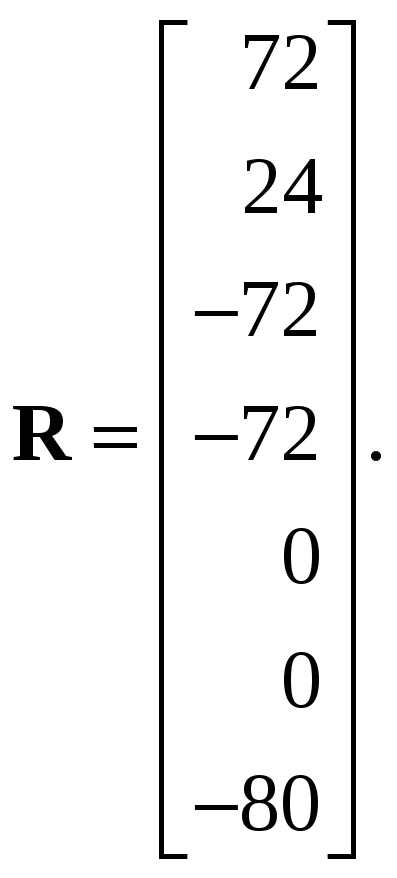
2. Решение

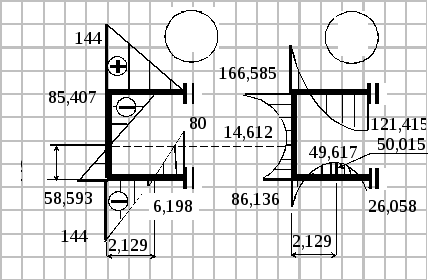
3. Экстремальное значение изгибающего момента в пределах элемента 4.

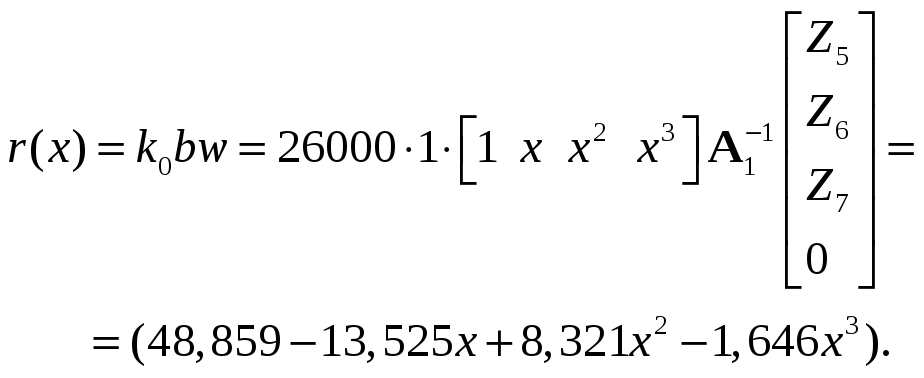
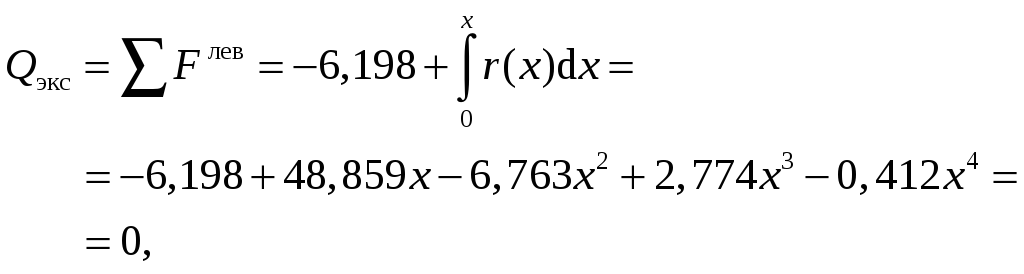
откуда x = 0,129 м.

Тогда

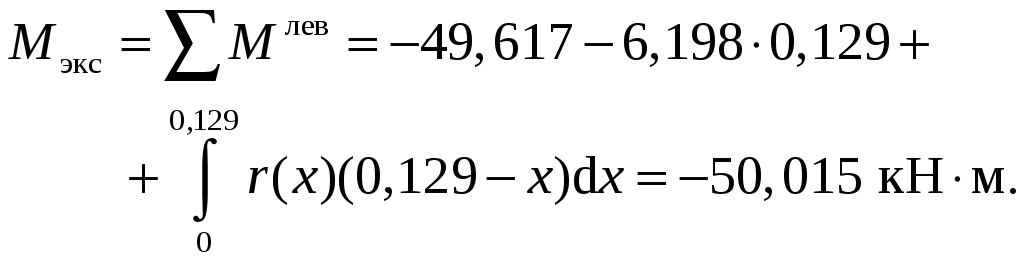
3. Прямоугольные плиты на упругом основании

1. Общие положения и составление системы разрешающих уравнений

Железобетонные плиты на упругом основании являются одним из наиболее важных конструктивных элементов промышленного, гражданского, гидротехнического и дорожного строительства, и поэтому необходимость наиболее точно отразить их напряженно – деформированное состояние является важной задачей теории сооружений.

В данном разделе рассмотрим расчет тонких плит, для которых справедливы гипотезы Кирхгофа-Лява. Материал плит считается идеально упругим и ортотропным.

При использовании МКЭ прямоугольная плита разбивается на ряд прямоугольных КЭ (рис. 8.12, а), соединенных между собой в узлах. При использовании метода перемещений в каждый узел полученной дискретной расчетной схемы вводятся дополнительные связи, припятствующие смещениям в трех направлениях: углам поворота в направлении координатных осей и вертикальному перемещению перпендикулярно срединной поверхности плиты (рис. 8.12, б). Углом поворота в плоскости плиты пренебрегают. Следовательно, состояние любого узла n КЭ (рис. 8.13) может быть характеризовано тремя узловыми силами и темя перемещениями:

(8.57)

Таким образом, матрица жесткости такого элемента будет 12-го порядка, и ее удобно представить в блочной форме:

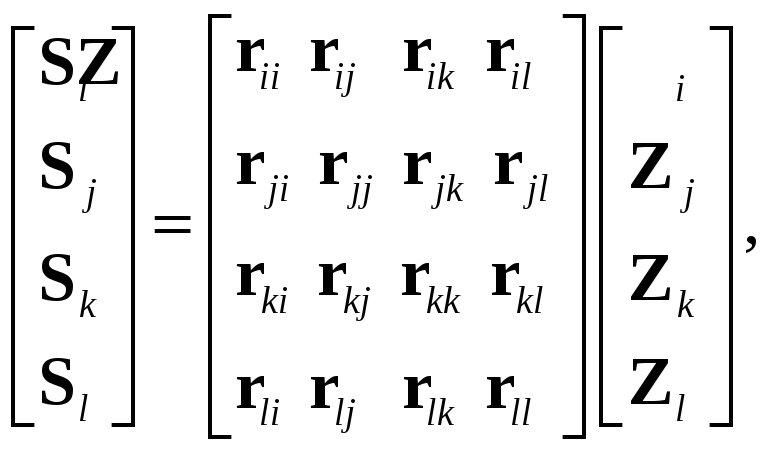(8.58)

или в краткой форме для КЭ

S_g = r_gZ_g. (8.59)

Представление матрицы жесткости в блочной форме позволяет отказаться от использования единого матричного алгоритма при составлении системы разрешающих уравнений. Использование матричного алгоритма не всегда удобно, так как матрицы преобразования деформаций, входящие в выражение (8.31), содержат большое число нулей (см. примеры 8.2 и 8.3), что излишне загромождает память ЭВМ при их использовании. Поэтому при составлении системы уравнений метода перемещений удобнее использовать блочный принцип.

Предположим, что все перемещения находятся в единой системе координат, которая в общем случае может не совпадать с направлениями координатных осей, принятых для отдельных элементов. Обозначим перемещения узлов и узловых сил в общей системе координат как Z_n* и S_n*. Для плит эти матрицы будут трехмерными [см. (8.57)]. Чтобы перейти к составлению матрицы K (8.27), для каждого элемента вводятся матрицы преобразования координат, с помощью которых матрицы Z_n и S_n заменяются матрицами Z_n* и S_n*. Например, для узла i S_i =a_i S_i*, Z_i = a_i Z_i*. В случае совпадения единой системы координат с системами координат отдельных элементов матрицы преобразования координат будут единичными.

Значения Z_n и S_n, выраженные через Z_n* и S_n*, подставляются в в (8.58), например, для первой строки:

или после умножения слева на ,

(8.60)

где выражения в скобках являются блоками матрицы K, составляемой для общей системы координат.

Рассмотрим часть области плиты, поделенной на прямоугольные конечные элементы (рис. 8.14), и составим уравнение равновесия для узла n:

(8.61)

где R_n – матрица свободных членов для узла n.

Подставив выражения для S* на основании (8.60) в (8.61), получим:

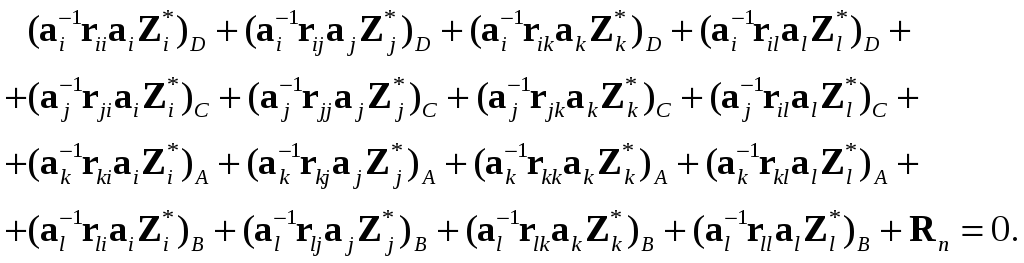(8.62)

На основании совместности деформаций в узлах дискретной схемы плиты для узла n (см. рис. 8.14)

(8.63)

Подставив (8.63) в (8.62) получим:

(8.64)

где выражения в круглых скобках

(8.65)

Уравнения типа (8.64) составляются для каждого узла: результатом объединения этих уравнений является выражение (8.27).

При совпадении местных систем координат, принятых для каждого отдельного элемента, с общей системой матрицы преобразования координат будут единичными и тогда В этом случае блоки матриц жесткости можно сразу (без преобразования) из (8.58) подставлять в (8.64).

Граничные условия для расчетной схемы учитываются при составлении блоков матриц усилий и перемещений (см. 8.57), определяемых для каждого граничного элемента.