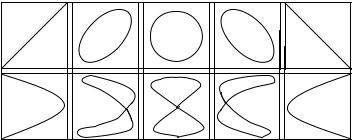
Если частоты складываемых, взаимно перпендикулярных колебаний различны, то замкнутая траектория результирующего колебания имеем сложный вид и носит названия фигур Лиссажу. Ж. Лиссаж – (1822-1880) – французский физик (см. рис. 11.4.)

Форма этих кривых зависит от соотношения амплитуд, частот и разности фаз складываемых колебаний. Отношение частот складываемых колебаний равно отношению числа пересечений фигур Лиссажу с прямыми, параллельным осям координат. По виду фигур можно определить неизвестную частоту по известной или определить отношение частот складываемых колебаний. Метод фигур Лиссажу используют для анализа соотношений частот и разности фаз складываемых колебаний.

1:2

Рис. 11.4. Виды фигур Лиссажу

Вопросы для повторения

1.Какие колебания называются вынужденными?

2.По какому закону изменяется амплитуда вынужденных колебаний?

3.Какой зависимостью связаны: циклическая частота вынужденных колебаний, частота собственных свободных колебаний и коэффициент затухания?

4.Какое явление называется резонансом?

5.Какая величина называется статическим отклонением?

6.Что такое биения?

7.Когда они возникают?

8.По какому закону изменяется амплитуда биений?

9.Чему равен период биений?

10.Какова траектория точки, участвующей одновременно в дух взаимно перпендикулярных колебаниях с одинаковыми периодами?

11.Какова траектория точки, участвующей одновременно в дух взаимно перпендикулярных колебаниях с одинаковыми периодами и одинаковыми амплитудами?

12.Когда в качестве траектории при сложении двух взаимно перпендикулярных колебаний получается прямая?

13.Как по виду фигур Лиссажу можно определить отношения частот складываемых колебаний?

Глава 18. Упругие волны

§12. Волны. Плоская стационарная волна

Процесс распространения колебаний в пространстве называется волной.

29

При распространении волны частицы среды не движутся вместе с волной, а колеблются около своих положений равновесия.

Вместе с волной от частицы к частице передается лишь состояние колебательного движения и его энергия.

Основное свойство всех волн не зависимо от их природы: перенос энергии осуществляется без переноса вещества.

Волны могут быть упругими, электромагнитными и на поверхности жидкости.

Упругими механическими волнами будем называть механические возмущения, распространяющиеся в окружающей среде.

Упругие механические волны делятся на продольные и поперечные.

В продольных волнах частицы среды колеблются в направлении распространения волны. В поперечных - в направлениях, перпендикулярных распространению волны. В жидкостях и газах возникают только продольные механические волны, в твердых телах - и продольные и поперечные механические волны.

Упругая волна называется гармонической, если соответствующие ей колебания являются гармоническими.

Фронтом волны называется геометрическое место точек, до которых дошли колебания в данный момент времени ( t ) .

Фронт волны представляет собой ту поверхность, которая отделяет часть пространства, уже вовлеченную в волновой процесс от области пространства, в которой колебания еще не возникли.

Волновой поверхностью можно назвать геометрическое место точек, колеблющихся в одинаковой фазе.

Волновых поверхностей существует бесконечно много, а волновой фронт для каждого момента времени один.

Волны, волновые поверхности которых представляют собой плоскости, называют плоскими. Если волновая поверхность имеет сферическую форму, волна называется сферической.

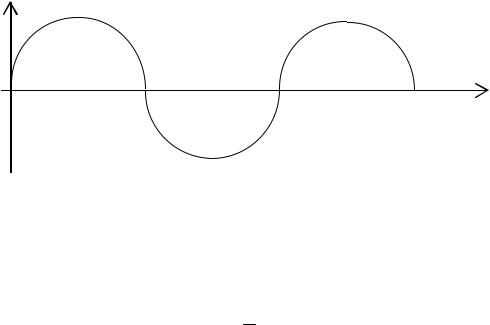
Через ξ – ( кси ) обозначим смещение частицы из положения равновесия. Тогда ξ = f (x) – будет график волны.

ξ

х

Рис 12.1. График волны дает зависимость смещения всех частиц среды от расстояния до источника в данный момент времени.

Расстояние, на которое переместилась волна за 1 период, называется длиной волны.

но

ν = T1 ;

30

λ = Vν

Будем рассматривать плоскую волну, имеющую гармонический характер, распространяющуюся в положительном направлении оси х.

Пусть через время τ плоская волна приходит в точку с координатой х, а распространяется со скоростью V.

Тогда:

Уравнение (13.5) является уравнением плоской волны, распространяющейся в положительном направлении оси х.

Зафиксируем какое-либо значение фазы колебания. Пусть фаза колебания является постоянной.

Сначала выразим время t, а затем продифференцируем это выражение по времени:

Из уравнения (13.8) следует, что V – скорость перемещения фазы волны (фазовая скорость).

ξ(x,t) = Acos(ωt −k x +ϕ) .

Распространение волн в однородной изотропной среде, в общем случаи, записывается уравнением в частных производных:

31

Пусть r – расстояние от центра волны до рассматриваемой точки среды. Тогда:

уравнение сферической волны.

§14. Принцип суперпозиции. Групповая скорость

Cреда называется линейной, если ее свойства не изменяются под действием возмущений, создаваемых волной.

Для линейных сред применим принцип суперпозиции (наложения) волн:

При распространении в линейной среде нескольких волн каждая из них распространяется так, как будто других волн не было, а результирующее смещение частицы среды в любой момент времени равно геометрической сумме смещений, которые получают частицы, участвуя в каждом из слагающих волновых процессов.

Любую волну (согласно принципу суперпозиции и разложению Фурье) можно представить в виде суммы гармонических волн, или группы волн.

Волновым пакетом называется суперпозиция волн, мало отличающихся друг от друга по частоте, занимающая в каждый момент времени ограниченную область пространства. Пусть простейший волновой пакет состоит из 2-x распространяющихся вдоль положительного направления оси х гармонических волн с одинаковыми амплитудами, близкими частотами и волновыми числами, причем dω<< ω и dk<< k.

Рассмотрим случай, когда в среде распространяется несколько волн одновременно. Тогда колебание частицы среды оказывается геометрической суммой колебаний, совершаемых каждой из всех волн в отдельности.

Волны называются когерентными, если разность фаз остается постоянной или изменяются по вполне определенному закону.

В результате наложения когерентных волн в разных точках пространства возникают максимумы и минимумы интенсивности, т.е. происходит перераспределение интенсивности.

32