M = −mglα , |
(4.8) |
|||||
т.к. угол α мал, то α sin α. |
|
|
|
|
||
Или |
|
|
|
|
||
– mgl α = J α , |
|
|||||
тогда |
|
|
|
|
||
α + |
mgl |
α = 0 |
(4.9) |
|||
|
||||||
|
J |
|
|
|
|
|
1 = |
|
J |
|
|||
ω0 |
|
mgl |
|
|||
или |
|
|
|
|
||
ω0 = |
|
mgl , |
(4.10) |
|||
|
|
|
J |
|
||
тогда |
|
|
|
|
||
Tфм = 2π |
|
J |
(4.11) |
|||
|
|
|
mgl |
|
||
L = |
|
J |
|
(4.12) |
||
ml |
||||||
|
|
|
||||
приведенная длина маятника, т.е. L – длина такого математического маятника, период колебаний которого равен периоду колебаний физического маятника.
Точка О′, отстоящая от точки О на продолжении прямой ОС на расстоянии приведенной длины L, называется центром качаний физического маятника.
По теореме Штейнера I = Ic + ml2 , тогда
L = |
Jc + ml |
= l + |
Jc |
> l , |
(4.13) |
|
ml |
ml |
|||||
|
|
|
|
т.е. ОО′ всегда больше ОС.
Точка качаний и точка подвеса обладают свойством взаимозаменяемости.
§5. Фазовый портрет маятника. Адиабатический инвариант
Рассмотрим опять колебания пружинного маятника. Энергия системы определяется, как мы уже видели, следующим выражением:
W =W +W = |
kx |
2 |
+ |
mx |
2 |
= const . |
(5.1) |
|
|
|
|
||||
p к |
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
Введем вместо скорости импульс: р= mx´. Тогда равенство (5.1) можно переписать в таком виде:
|
|
p2 |
|
kx |
2 |
|
|
(5.2) |
||
|
|
|
|
+ |
|
|
=W . |
|||
|
|
2m |
2 |
|||||||
|
|
|
|
|
|
|
||||
Разделим это равенство на W: |
|
|
|
|
|
|
|
|||
|
|
p2 |
|
+ |
kx2 |
=1 |
, |
(5.3) |
||
|
2mW |
2W |
||||||||
|
|
|
|
|
||||||
или
10
|
p |
|
2 |
|
x |
2 |
|
|
|
|
|
= 1. |
(5.4) |
||||
|
|
|
|
+ |
|
|
||
|
|
|
|
|
2W |
|
|
|
|
2mW |
|
|
|
||||
|
|
|
|
|
|
k |
|
|
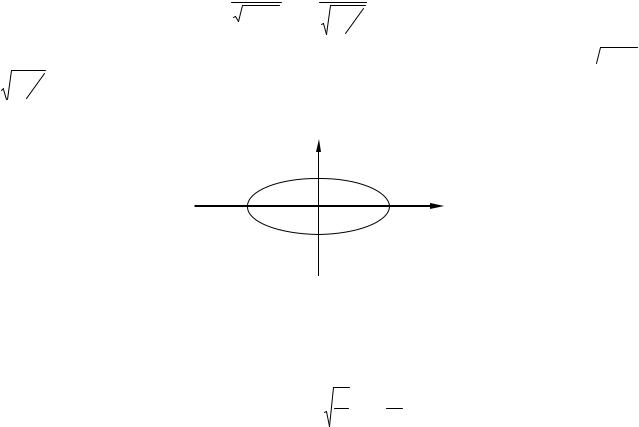
В«пространстве» с координатными осями x и p это уравнение эллипса с полуосями 
2mW
и2W k . Пространство с осями «координата - импульс» называется фазовым пространством системы.
y
0 |
x |
Рис 5.1. Траектория гармонического осциллятора в фазовом пространстве.
Таким образом, траектория гармонического осциллятора в фазовом пространстве представляет собой эллипс. А площадь эллипса, задаваемого уравнением: x²/a2+y²/b2=1. равна S = π a b, тогда площадь под фазовой траекторией определяется выражением:
S =πab = 2πW |
m |
= 2π W |
, |
(5.5) |
|||
|
|
|
k |
ω |
|
|
|
или |
|
|
|
|
|
|
|
|
S |
= |
W |
. |
|
|
(5.6) |
|
2π |
|
|
|
|||
|
|
ω |
|
|
|
||
Величина площади S, заключенной внутри фазовой траектории частицы, деленная на 2π, имеет в физике специальное название- адиабатический инвариант. Для гармонического осциллятора адиабатический инвариант определяется выражением:
I = |
S |
= |
W |
. |
(5.8) |
2π |
|
||||
|
|
ω |
|
||
Величина I была названа адиабатическим инвариантом потому, что мы рассматривали движение при неизменных параметрах системы, то есть приколебаниях пружинного маятника (грузика на пружинке) неизменным параметрами были масса грузика и коэффиицент жесткости пружинки, т.е. величина k, а значит и частота ω.
Равенство (5.8) справедливо не только для колебаний грузика на пружинке, но и для любой другой системы, совершающей гармонические колебания, параметры которой испытывают медленные вариации со временем. Например, это может быть математический маятник, длина которого медленно меняется со временем.
Вопросы для повторения
1.Что называется:
2.гармоническим осциллятором?
3.Пружинным, физическим, математическим, маятником?
4.Приведенной длиной физического маятника, центром качений?
5.фазовым пространством системы?
11