|
|
2πк |
μμ0 IR 2πR |
|||
Bz = ∫ dBz = μμ0 I cosϕ/ 4πr |
2 |
∫ dl = |
||||
|
4π(R |
2 |
+ z |
3/ 2 |
||
|
|
0 |
|
2 ) |
||
1)Если z = 0 (т.е. в точке О), то:
= |
μμ0 IR2 |
|
|
. |
|
2 (R2 + z2 )3/ 4 |
||
B0 = μμ2R0 I – магнитная индукция поля, создаваемого кольцом с током.
2) |
При z >> |
R Bz = |
μμ0 R2 I |
; |
|||
2 z3 |
|||||||
При μ = 1 |
B |
= |
μ0 I |
. |
|
|
|
|
|
|
|||||
|
|
0 |
|
2R |
|
|
|
|
|
|
|
|
|
||
§29. Теорема Гаусса для поля вектора B
МП обладает двумя важнейшими свойствами, они связаны с потоком и циркуляцией и выражают основные законы МП.
Основными законами МП являются: теорема Гаусса и теорема о циркуляции.
1. Поток вектора B . Теорема Гаусса для поля B .
Потоком вектора МП через площадку dS называется скалярная величина dΦ, равная
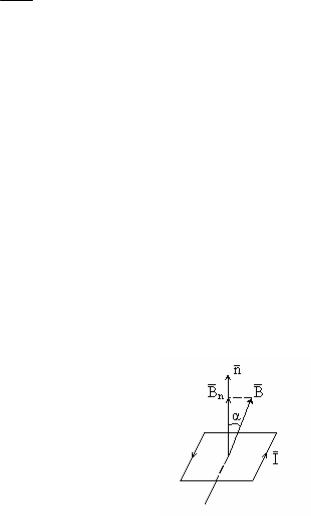
Рис. 29.1 |
|
dΦВ = В dS , |
(29.1) |
или |
|
dΦВ = В dS cos α, |
(29.2) |
Bn = B cos α .
dSG = dSnG – вектор, модуль которого равен dS , а направление совпадает с ( nG) нормалью к площадке.
Поток вектора B МП может быть как положительным, так и отрицательным.
Положительное направление нормали связано с направлением тока правилом правого винта.
Магнитный поток, создаваемый контуром, через поверхность, ограниченную им самим, всегда положителен.
25
ΦB = ∫ BnGdS = ∫ BdS |
(29.3) |
|
S |
S |
|
G G
Если B dS , то ΦB = BS . [Фв] = 1Вб = 1Тл · 1м2
1 вебер – это магнитный поток, проходящий через поверхность, ограниченную им самим, всегда положителен.
Теорема Гаусса для поля B : поток вектора B сквозь любую замкнутую поверхность равен
нулю. |
|
∫ BdS = 0 |
(29.4) |
S |
|
Теорема Гаусса является обобщением опыта. Она как постулат выражает эксперименталь-
ный факт, что линии B не имеют ни начала, ни конца, т.е. МП не имеет источников.
Число линийB , выходящих из любого объема, ограниченного замкнутой поверхностью
S, всегда равно числу линий, входящих в этот объем.
Поток вектораB сквозь замкнутую поверхность S, ограниченную некоторым замкнутым контуром, не зависит от формы поверхности S.
Формула (29.4) выражает тот факт, что в природе нет магнитных зарядов, т.е. МП не имеет источников.
§30. Теорема о циркуляции вектора B для поля постоянных токов в вакууме
(или закон полного тока)
|
Циркуляцией вектора В по заданному контуру называется интеграл: |
|
|
|
∫ Bdl = ∫ Bl dl , |
(30.1) |
|
|
L |
L |
|
где |
G |
|
|
dl – элементарный вектор длины контура, направленный вдоль контура. |
|
||
|
|
Bl =B cos α , |
(30.2) |
где |
Вl – составляющая вектора B в направлении касательной к контуру; |
|
|
α = (B,dl ) – угол между векторами B и dl . |
|
||
|
Теорема о циркуляции B , или закон полного тока (для МП постоянных токов в вакууме): |
||
|
Циркуляцией вектора B по произвольному замкнутому контуру L в вакууме равна произве- |
||
дению μ0 на алгебраическую сумму токов, охватываемых контуром L. |
|
||
|
|
∫ Bdl = μ0 I , |
(30.3) |
|
|
L |
|
где
26
N |
|
I = ∑ Ii , |
(30.4) |
i=1
где сила тока, величина алгебраическая, N – число проводников с токами, охватываемых контуром L.
Каждый ток учитывается столько раз, сколько он охватывается контуром. Ток считается положительным, если его направление связано с направлением обхода правилом правого винта. Ток противоположного направления считается отрицательным.
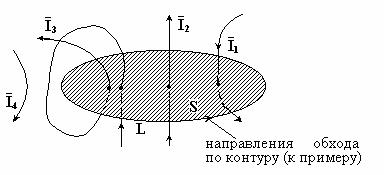
Рис. 30.1
Например: (смотри рис. 30.1)
N |
|
∑Ii =−I1+ I2 + I3 + I3 − I4 0 = I2 +2 I3 − I1 |
(30.5) |
i=1
Выражение (30.5) справедливо только для поля в вакууме. Формула (30.3) – постулат, подтвержденный экспериментально.
Если ток I распределен по объему, то
I = ∫ jdS, |
(30.6) |
где S – произвольная поверхность, натянутая на контур. И тогда (30.3) можно записать так: |
|
∫BdI= μ0 SjdS= μ0 j0dS |
(30.7) |
L |
|
Факт, что циркуляция вектора B , вообще говоря, не равна нулю, означает, что поле B не потенциально. Поле B называют вихревым или соленоидальным.
Закон (30.7) называют еще законом полного тока.
Теорема о циркуляции вектора B играет примерно такую же роль, что и теорема Гаусса для векторов E и D .
Но циркуляция B определяется только теми токами, которые охватывают данный кон-
тур. При наличии специальной симметрии теорема о циркуляции оказывается весьма эффек-
тивной, позволяя очень просто находить B .
27