
Задачи ЛП и методы их решения
.pdf
159
Можно показать, что решение такой целочисленной задачи существует[22]. Так как кратности элементов остатка вектора требований b[M ] – небольшие и мы знаем число съемов в оптимальном решении, то комбинаторный метод не займет много времени.
Задача о минимальном количестве перенастроек ПРС
Как уже упоминалось, для получения решения задачи линейного раскроя применяется модифицированный симплекс метод, и оптимальным решением является нецелочисленная линейная комбинация, состоящая из m линейно независимых способов раскроя. Как правило, в этой линейной комбинации векторов все коэффициенты отличны от нуля и большинство из них не целочисленные, т.е. в решении, полученном на втором шаге, будет использовано большое количество съемов (максимальное количество съемов на втором шаге m −1). Как показало тестирование комбинированного метода, все способы раскроя, полученные на втором шаге, различны и не совпадают со способами раскроя полученными в МСМ. Это приводит к тому, что в конечном оптимальном целочисленном решении используется число различных способов раскроя, как правило, превосходящее число раскроев в базисном решении нецелочисленной задачи.
На практике, каждый новый способ раскроя означает предварительную настройку ПРС, что требует дополнительного времени и усилий персонала. Поэтому число различных раскроев участвующих в решении, по возможности нужно свести к минимуму.
Поэтому возникает следующая задача: среди всех оптимальных решений целочисленной задачи раскроя выбрать то, которое содержит наименьшее число различных способов раскроя, т.е. минимизировать число перенастроек ПРС.
Итак, пусть f * оптимальное значение целевой функции ЗЛР. Рассмотрим набор векторов x[N] такой, что
f (x[N]) = f *
A[M, N] x[N] = b[M ] x[N] ≥ 0[N]
x[N] – целочисленный.
Каждая положительная компонента x[i] вектора интенсивностей x[N] означает использование в решении i -го способа раскроя. Следовательно, задача минимизации числа различных способов раскроя участвующих в решении равносильна минимизации положительных компонент вектора x[N], т.е. нам необходимо найти самое вырожденное решение исходной задачи. Обычно складывается кардинально противоположная ситуация – вырожденных решений стараются избегать.
Как говорилось выше, решение, получаемое на втором шаге комбинированного метода, состоит из различных способов раскроя, поэтому оптимизацию по числу различных способов раскроя имеет смысл вести только на первом шаге решения задачи, который представляет собой МСМ.
Различным оптимальным решениям МСМ соответствуют различные базисные подматрицы, в которых все столбцы имеют нулевую оценку. Если мы переберем все возможные такие подматрицы, то, очевидно, мы переберем все решения и выберем наилучшее.
Добавим, к уже имеющимся ограничениям еще одно 1[N] x[N] ≥ K
Это условие означает, что значение целевой функции не опустится ниже оптимального целочисленного значения. Так как целевая функция непрерывна и ее минимальное значение без дополнительного условия меньше либо равно K , то оптимальным значением целевой функции в новой задаче будет K , т.е. обязательно целое значение.

160
Следовательно, среди решений этой задачи могут быть и полностью целочисленные, и, если они существуют, то при полном переборе решений мы обязательно их найдем и выберем наилучшее. Базисность целочисленного решения рассматривается в[22].
Добавление одного дополнительного условия, увеличивает размерность решаемой задачи на единицу. Т.е. размерность задачи уже не m , как было раньше, а m +1. Также, при решении этой задачи с помощью МСМ добавится еще одна переменная x[n +1] с нулевым коэффициентом в целевой функции и один «пустой» способ раскроя rn+1 = A[M,n +1] = (0,0,...,0,−1).
Таким образом, приходим к следующей расширенной задаче линейного
программирования |
|
|
|
||
f (x[N]) = 1[N] x[N] → min |
|
||||
|
|
0 |
|
|
|
|
A |
|
|
|
|
|
|
|
|
||
|
|
|
|
x[N,{n +1}] |
= b[M ] |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
−1 |
|
|
||
X[N] ≥ 0[N]
Среди решений этой задачи, необходимо найти то, которое дает самое вырожденное решение исходной целочисленной задачи.
Рациональная загрузка ПРС
Постановка задачи
Форматный раскрой бумажного полотна, осуществляется на продольно-резательных станках (ПРС), которые могут иметь различные технические характеристики (основными из которых являются производительность ( m ) и время перенастройки(t )). Пусть буммашину обслуживают два ПРС со следующими характеристиками:
Наименование |
Производительность |
Время |
Время на ремонт |
|
ПРС |
перенастройки |
|||
|
|
|||
ПРС-1 |
m1 |
t1 |
T1 |
|
|
|
|
|
|
ПРС-2 |
m2 |
t2 |
T2 |
|
|
|
|
|
Необходимо распределить между этими двумя ПРС для разрезания S съемов, среди которых имеется R различных съемов (равно общему числу перенастроек ПРС). Выбранное распределение съемов между ПРС и условия, которые должны выполняться приведены в таблице
Наим. ПРС |
Кол-во съемов |
Кол-во |
|
Общее время |
|||||||
перенастроек |
|
|
|
работы |
|
||||||
|
|
|
|
|
|
||||||
ПРС-1 |
x |
u |
|
t(1) |
= |
|
x |
|
+ ut |
+T |
|
|
|
|
|||||||||
|
p |
|
|
m1 |
1 |
1 |
|||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
ПРС-2 |
y |
v |
|
t(p2) |
= |
|
y |
|
+ vt2 +T2 |
||
|
m2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||||
Условия |
x + y = S |
u + v = R < 2M |
|
t(p1) |
−t(p2) |
|
→ min (*) |
||||
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|

161
Покажем, что минимум в (*) равен нулю и достигается при t(p1) = t(p2) = T0 . Для простоты, будем считать, что T1 = T2 = 0 . При уменьшении t(p1) за счет уменьшения x , величина y на столько же увеличится, и может (не обязательно) увеличиться v. Следовательно, увеличится и t(p2) , и станет больше T0 . При уменьшении t(p1) за счет изменения u , t(p2)
увеличится за счет увеличения хотя бы на один съем y ( v может и не увеличиться, если такой съем режется и на 2-м ПРС). Таким образом, при выполнении условия t(p1) = t(p2) = T0
минимум в (*) равен нулю.
Подсчитаем распределение отрезаемых съемов между ПРС в частном случае, когда все съемы различны и имеются в одном экземпляре. Тогда:
1). x + y = S ; 2). u + v = R ; 3). S = R ; 4). u = x, v = y
5). |
x |
+ x t = |
S − x |
+ (S − x) t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1 |
m2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
m1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
m2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
x |
* |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S, |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
+ t2 |
+ |
1 |
|
|
|
+ |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
t1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
m1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
(*) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t1 + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
y |
* |
= S − x = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S. |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ t2 |
+ |
|
|
|
1 |
|
+ |
|
|
1 |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
m1 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m2 |
|
|
|||||||||||||||||
Время работы обоих ПРС |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
+ |
|
|
|
|
|
t |
2 |
+ |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m2 |
|
|
||||||||||||||
|
|
|
|
|
|
t |
(1) |
|
= t |
(2) |
|
= |
|
|
|
|
|
|
|
|
|
|
m1 |
|
|
|
|
|
|
|
|
. |
||||||||||||||||||
|
|
|
|
|
|
p |
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
+t |
2 |
+ |
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
m1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m2 |
|
||||||||||||||
Отношение отрезаемых съемов и числа перенастроек |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
+ |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
x* |
|
|
u* |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
= |
= |
|
|
|
|
|
|
|
|
m |
2 |
|
|
|
≈ |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
. |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
y* |
|
v* |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m2 |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t1 + m |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Алгоритм решения задачи
Итак, пусть имеются два станка, на которых обрабатываются n различных типов деталей (раскладок) в количестве S = α[N] 1[N] ( N = n) штук съемов. Время обработки деталей на станках пропорционально их (деталей) количеству ( x t1 и y t2 соответственно). Время перенастройки станков на обработку деталей другого типа линейно зависит от количества деталей разных типов, обрабатываемых на станке (u τ1 и v τ2 соответственно).
Напомним, что требуется найти загрузку станков, дающую минимум модуля разности общего времени работы ПРС-1 и ПРС-2, т.е.

163
и начнем работу алгоритма с варианта «ноль-всё» (все детали обрабатываются на одном из станков). Теперь перебрасываем детали с небольшими кратностями (сначала с единичными) из нижней части списка деталей. Это обеспечивает большие значения скачка целевой функции f . Когда в (**) левая и правая части станут примерно одинаковыми, начинаем перебрасывать детали с большими кратностями (из верхней части списка деталей). Теперь (**) не изменяется, а обе части в (*) подравниваются.
В соответствие с описанным алгоритмом рассчитан нижеследующий пример:
ПРИМЕР 1.
Рассмотрим оптимальные раскладки (номер раскладки и количество вырезаемых съемов по ней см. столбцы 12 и 13) по заявке 034 от 27.09.04 БМ21, подлежащие распределению между ПРС-1 и ПРС-7.
Всего съемов: S=126 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Различных раскладок: n=31 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
ПРС-1: t1 = 2t, |
τ1 =10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ПРС-7: t2 = t, τ1 = 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1 |
|
2 |
3 |
4 |
|
5 |
6 |
|
|
|
7 |
|
8 |
9 |
10 |
|
|
12 |
|
13 |
|
|||||
|
n |
i |
x |
u |
|
Δt |
|
Tпрс1 |
|
|
y |
|
v |
Δt |
|
Tпрс1 |
Δtпрс |
|
|
|
|
|
|
|||
1 |
|
31 |
1 |
1 |
|
2t+10 |
|
2t+10*1 |
|
|
125 |
|
30 |
-(t+4) |
|
125t+30*4 |
123t+110 |
1 |
|
32 |
|
|||||
|
2 |
|
30 |
2 |
2 |
|
2t+10 |
|
4t+10*2 |
|
|
|
124 |
|
29 |
-(t+4) |
|
124t+29*4 |
|
120t+96 |
|
2 |
|
|
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
3 |
|
29 |
3 |
3 |
|
2t+10 |
|
6t+10*3 |
|
|
123 |
|
28 |
-(t+4) |
|
123t+28*4 |
117t+82 |
3 |
|
10 |
|
|||||
. |
|
… |
. |
. |
… |
|
… |
|
|
… |
|
… |
… |
|
… |
… |
|
|
|
|
|
|
||||
8 |
|
24 |
8 |
8 |
|
2t+10 |
|
16t+80 |
|
|
118 |
|
23 |
-(t+4) |
|
118t+92 |
102t+12 |
5 |
|
7 |
|
|||||
9 |
|
1 |
9 |
9 |
|
2t+10 |
|
18t+90 |
|
|
117 |
|
23 |
-(t+4) |
|
117t+92 |
99t+2 |
6 |
|
6 |
|
|||||
10 |
|
1 |
10 |
9 |
|
2t |
|
20t+90 |
|
|
116 |
|
23 |
-t |
|
116t+92 |
96t+2 |
7 |
|
5 |
|
|||||
|
|
. |
… |
. |
. |
… |
|
… |
|
|
|
… |
… |
… |
|
… |
|
… |
|
|
|
|
|
|
||
39 |
|
1 |
39 |
9 |
|
2t |
|
78t+90 |
|
|
87 |
|
23 |
-t |
|
87t+92 |
9t+2 |
8 |
|
5 |
|
|||||
40 |
|
1 |
40 |
9 |
|
2t |
|
80t+90 |
|
|
86 |
|
22 |
-(t+4) |
|
86t+88 |
6t-2 |
9 |
|
4 |
|
|||||
41 |
|
2 |
41 |
10 |
|
2t+10 |
|
82t+100 |
|
|
85 |
|
22 |
-t |
|
85t+88 |
3t-12 |
10 |
|
4 |
|
|||||
42 |
|
2 |
42 |
10 |
|
2t |
|
84t+100 |
|
|
84 |
|
22 |
-t |
|
84t+88 |
-12 |
11 |
|
3 |
|
|||||
43 |
|
2 |
43 |
10 |
|
2t |
|
86t+100 |
|
|
83 |
|
22 |
-t |
|
83t+88 |
-3t-12 |
12 |
|
3 |
|
|||||
44 |
|
31 |
42 |
9 |
|
-2t-10 |
|
84t+90 |
|
|
84 |
|
23 |
t+4 |
|
84t+92 |
2 |
13 |
|
2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
42 съема 9 перенастроек |
|
|
|
|
84 съема 23 перенастройки |
15 |
|
2 |
|
||||||||||||||
|
|
|
30 |
1 |
|
|
|
|
|
|
|
|
2 |
|
12 |
|
|
|
|
|
16 |
|
2 |
|
||
|
|
|
29 |
1 |
|
|
|
|
|
|
|
|
3 |
|
10 |
|
|
|
|
|
17 |
|
1 |
|
||
|
|
|
… |
… |
|
|
|
|
|
|
|
|
4 |
|
9 |
|
|
|
|
|
|
… |
|
… |
||
|
|
|
24 |
1 |
|
|
|
|
|
|
|
|
5 |
|
7 |
|
|
|
|
|
31 |
|
1 |
|
||
|
|
|
1 |
32 |
|
|
|
|
|
|
|
|
6 |
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
2 |
3 |
|
|
|
|
|
|
|
|
7 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tпрс1=84t+90 |
|
|
|
|
|
Δtпрс=2 |
|
|
|
tпрс7=84t+92 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|

165
|
20 |
|
1 |
|
1 |
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
3 |
|
|
4 |
|
|
6 |
|
|||
|
|
|
|
|
|
|
|
|
|||||
1 |
5 |
|
1 |
|
0 |
|
0 |
|
1 |
||||
|
|
|
|
|
|||||||||
|
2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
5 |
|
0 |
1 |
|
|
0 |
|
0 |
||||
|
|
|
|
|
|
||||||||
|
3 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
9 |
5 |
|
0 |
0 |
|
1 |
|
|
0 |
||||
|
|
|
|
|
|||||||||
|
|
4 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
5 |
|
0 |
0 |
|
1 |
|
|
1 |
|
|||
|
|
|
|
|
|
|
|||||||
|
|
6 |
|
|
6 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
Текущее базисное решение оптимально.
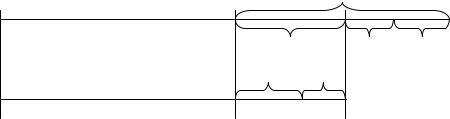
Сформируем матрицу числа перестановок ножей при переходе от одной раскладки к другой. Для этого графически изобразим матрицу базисных раскроев. Очевидно, что переход от одной перенастройки к другой и обратно является процессом симметричным. Тогда матрица числа перестановок ножей будет следующей симметричной матрицей:
Х |
2 |
2 |
4 |
|
|
|
|
|
|
|
|
Х |
2 |
2 |
4 |
|
|
|
|
|
2 |
Х |
3 |
3 |
|
|
|
|
|
2 |
3 |
Х |
4 |
|
|
|
|
|
4 |
3 |
4 |
Х |
|
|
2 |
Х |
3 |
3 |
|
|
|
|
|
|
|
|
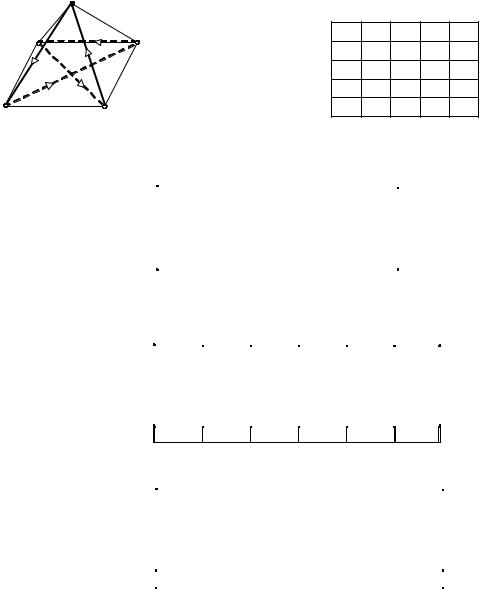
Если рассмотреть полный граф |
M, N , где |
M – множество |
|||
|
|
|
базисных раскроев, |
N – |
множество |
переходов |
между |
|
|
|
|
раскроями (u – перенастройка с раскроя |
i(u) |
на раскрой |
j(u) ). |
||
|
|
|
Тогда данная матрица будет матрицей длин дуг |
|||||
|
|
|
рассматриваемого полного графа. |
|
|
|
||
2 |
3 |
Х |
4 |
2 |
2 |
|
|
|
|
|
|
1 |
|
|
|
||
|
|
|
|
|
|
|
||
|
|
|
|
2 |
|
|
|
|
|
|
|
4 |
|
3 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
4 |
4 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, задача о минимальной суммарной перестановке ножей при перенастройке ПРС сводится к отысканию кратчайшего пути в данном графе, содержащем все его вершины по одному разу, т.е. гамильтонова пути.
167
|
0 |
1 |
2 |
3 |
|
1 |
1 |
Х |
0 |
0 |
|
2 |
1 |
0 |
Х |
1 |
|
3 |
1 |
0 |
1 |
Х |
|
4 |
0 |
1 |
0 |
1 |
|
|
|
|
|
|
|
Подсчитаем оценку для текущего решения |
(ω(Y) =16 ) |
и запретим переход, |
|||||||||
преждевременно замыкающий цикл |
C40 |
= ∞(×) . |
|
|
|
|
|
|
|||
Начинаем новую итерацию и приводим текущую матрицу |
|
|
|
|
|||||||
|
|
0 |
1 |
|
2 |
|
3 |
|
|
|
|
1 |
|
0 |
|
Х |
|
0 |
|
0 |
|
0 |
|
2 |
|
0 |
|
0 |
|
Х |
|
1 |
|
0 |
|
3 |
|
0 |
|
0 |
|
1 |
|
Х |
|
0 |
|
4 |
|
Х |
|
1 |
|
0 |
|
1 |
|
0 |
|
|
|
1 |
|
0 |
|
0 |
|
0 |
|
|
|
h(2) = 1 maxθ(ij) = θ(13) = 1 ω(Y ) = 17 +1 = 18 .
Вычеркиваем первую строку и третий столбец. Получаем приведенную матрицу
|
0 |
1 |
2 |
|
2 |
0 |
0 |
Х |
0 |
3 |
0 |
0 |
1 |
0 |
4 |
Х |
1 |
0 |
0 |
1 0 0
ω(Y) =16 . Запрещаем переход C31 = ∞(×). |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
Новая итерация. h(3) = 0 |
maxθ(ij) = θ(42) |
= 2 |
|
|
|
|
|
|
|
|
|
ω(Y |
) = 18 + 2 = 20. |
||||||||
Вычеркиваем строку 4 и столбец 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
|
|
||||
2 |
|
0 |
|
0 |
|
|
||||
3 |
|
0 |
|
|
|
Х |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Остается матрица 2× 2 , в которой возможны только переходы (3,0) и (2,1). Проверка на оптимальность показывает, что ω(Y) ≤ ω(Y ) для любого Y . Значит получен кратчайший гамильтонов контур длиной 18 0 → 4 → 2 →1→ 3 → 0 .
Удаляя из него вершину 0 вместе с инцидентными ей дугами (0,4) и (3,0), получаем искомый кратчайший гамильтонов путь 4 → 2 →1→ 3 длиной 8.
Таким образом, для вырезания всех необходимых форматов требуется четыре раза перенастроить ПРС. При этом нужно восемь раз переставить ножи на ПРС.
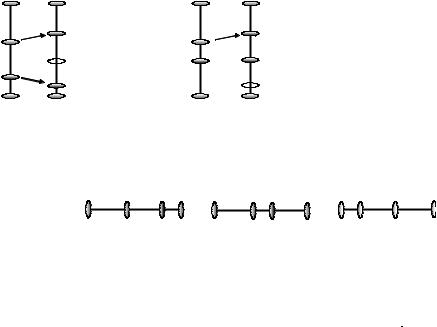
Следует отметить, что лексикографическое упорядочение форматов в раскладке само по себе не обеспечивает минимальности перестановок ножей при переходе от раскладки к раскладке. Это подтверждается следующим примером:
m = 3, L =10, l = (4,3,2) .
|
168 |
|
Рассмотрим раскладки R1 = (2,0,1) |
и |
R2 = (0,3,0) . При лексикографическом |
упорядочении длин для перехода от R1 к |
R2 |
требуется три перестановки ножей, а если |
заготовку длины 2 расположить между заготовками длины 4, то перестановок будет 2.
|
3 |
|
3 |
|
Это |
означает, |
что |
и |
|
4 |
4 |
|
гамильтонов |
|
контур |
||||
|
|
|
|
||||||
|
|
|
|
|
|
||||
|
3 три перестановки |
2 |
3 |
две перестановки |
минимальной |
длины |
для |
||
4 |
|
|
|
||||||
|
|
|
|
|
лексикографически |
||||
|
3 |
|
3 |
|
|
||||
|
4 |
|
упорядоченных |
|
раскладок |
||||
2 |
|
|
|
|
|||||
1 |
|
1 |
|
|
|||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
будет |
давать |
только |
||
некоторое субоптимальное решение. Будем в дальнейшем различать понятия "раскладка" |
|||||||||
(способ раскроя) и "расстановка ножей в раскладке". Одной раскладке может |
|||||||||
соответствовать несколько |
расстановок |
ножей, её реализующих. Так раскладке |
R1 из |
||||||
нашего примера соответствуют три способа расстановки ножей. |
|
|
|
|
|||||
4 |
4 |
2 |
4 |
2 |
4 |
2 |
4 |
4 |
А, если учесть симметрию, то две (последняя расстановка ножей симметрична первой).
ПРИМЕР 1: m = 3 |
|
L = 26, |
|
|
l = (9,6,4), |
b = (90,90,90) |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
8 |
|
|
|
9 |
|
|
10 |
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
1 |
|
1 |
|
1 |
|
0 |
|
|
0 |
|
0 |
|
0 |
|
0 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
1 |
|
|
0 |
|
2 |
|
1 |
|
0 |
|
4 |
|
|
3 |
|
2 |
|
1 |
|
0 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
0 |
|
|
2 |
|
1 |
|
2 |
|
4 |
|
0 |
|
|
2 |
|
3 |
|
5 |
|
6 |
|
|
||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
0 |
|
|
1 |
|
|
3 |
|
|
1 |
|
|
2 |
|
|
0 |
|
|
2 |
|
|
|
0 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Приведены только технологичные раскладки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
{ |
} |
2 |
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
– оптимальная базисная матрица. |
|||||||||||||||||||||||||||||||
N ' = |
|
2,7,9 , A[M , N '] = |
0 |
3 |
1 |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
2 |
2 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Рассмотрим в каждом способе раскроя все расстановки ножей (с учетом симметрии)
2 |
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
9 |
9 |
4 |
4 |
21 |
0 |
|
6 |
6 |
6 |
4 |
4 |
71 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
9 |
4 |
9 |
4 |
22 |
3 |
|
6 |
6 |
4 |
6 |
4 |
72 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
9 |
4 |
4 |
9 |
23 |
2 |
|
6 |
6 |
4 |
4 |
6 |
73 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
9 |
9 |
4 |
24 |
|
|
6 |
4 |
6 |
6 |
4 |
74 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
4 |
6 |
4 |
6 |
75 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
6 |
6 |
6 |
4 |
76 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
6 |
4 |
4 |
4 |
4 |
4 |
91 |
0 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
4 |
6 |
4 |
4 |
4 |
4 |
92 |
1 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
4 |
4 |
6 |
4 |
4 |
4 |
93 |
5 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

 2,1
2,1 3,1
3,1 4,1
4,1 6
6