Файловый архив студентов. Файловый архив студентов.
1261 вуз, 4614 предмет.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Сыктывкарский Государственный Университет им. Питирима Сорокина
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

Задачи ЛП и методы их решения

.pdf
Скачиваний:
155
Добавлен:
29.03.2016
Размер:
7.64 Mб
Скачать
☆

139

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

0

 

 

0

 

0

 

 

 

 

 

 

 

1

 

 

2

3

 

4

5

 

6

 

7

8

 

9

 

 

 

z[N ',6]= B[N ',M ] A[M,6]

=

 

 

 

 

 

 

=

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0

 

 

1

 

 

4

 

4

 

 

 

 

 

 

 

 

1

 

 

1

1

 

1

1

 

1

 

1

 

1

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5

1

 

 

100

 

 

2

 

 

2

1

 

1

1

 

0

 

0

 

0

 

0

 

 

 

Оценку ε[6] и

 

z[N ',6]

 

записываем

 

 

в

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

выделенный

 

(ведущий) столбец

основной

9

1

 

 

100

 

 

1

 

 

0

2

 

1

0

4

 

3

 

2

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

симплекс-таблицы

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

200

 

 

2

 

 

1

2

 

1

0

 

3

 

2

 

1

 

0

 

 

 

 

 

 

 

 

200

 

1

 

1

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5

 

 

 

100

 

1

 

0

 

 

 

 

0

 

 

 

 

 

 

Выбор

θ

определяет

 

номер

 

 

базисного

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

9

 

 

 

100

 

0

 

1

 

 

 

 

4

 

 

 

 

 

 

вектора

(строка

 

отмечается

 

 

стрелкой),

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

который будет выведен из базиса и заменен

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

на столбец, оценка которого нарушает

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

условие оптимальности

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

100

 

 

 

 

x[9]

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x[i]

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x[i]

 

 

 

 

 

 

 

 

100

 

 

 

x[9]

 

 

θ = min

 

 

 

 

 

z[i,6]>0 =

 

 

 

 

 

=

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

θ = min

 

 

 

 

 

 

z[i,6]>0 =

 

 

 

 

=

 

 

 

 

 

 

 

z

[

i,6

]

 

 

 

 

 

 

 

4

 

 

 

 

z

9,6

]

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

[

 

 

 

 

 

 

 

 

[

i,6

]

 

 

 

 

 

 

4

 

 

[

9,6

]

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

z

 

 

 

 

 

 

 

 

 

 

 

 

 

z

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(строка, соответствующая переменной x[9]

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(переменная x[9]

станет небазисной).

 

 

 

 

 

 

 

 

- ведущая)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Переход к новому решению:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Переход к новому решению:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

а) Заменяем в столбцах N ' и C[N ']

9 на 6

 

 

 

 

 

 

 

 

 

 

 

 

 

 

а) Заменяем в столбце N ' номер 9 на номер

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

и C[9]=1 на C[6]=1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

6

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

б) Делаем один шаг метода

 

полного

б) Выделенную часть основной симплекс-

исключения Гаусса-Жордана в выделенной

таблицы преобразуем по

методу

полного

части симплекс-таблицы с

 

 

 

ведущим

исключения Гаусса-Жордана с ведущим

элементом,

 

 

стоящим

 

на

 

 

пересечении

элементом

 

4

 

 

 

(ведущий

 

 

 

столбец

 

не

отмеченного столбца и отмеченной строки

заполняем).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Получаем новое базисное решение

 

 

 

 

Получаем новое базисное решение

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

2

3

4

5

6

7

8

9

 

 

 

 

 

 

 

 

 

 

 

 

1

1

1

1

1

1

1

1

1

 

 

125

 

1

 

1

 

 

 

 

 

 

 

 

 

 

 

 

5

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4

 

 

1

100

2

2

1

1

1

0

0

0

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5

 

100

 

1

 

0

 

 

6

1

25

1

0

2

1

0

1

3

2

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

6

 

25

 

0

 

1

 

 

 

 

 

4

 

4

4

 

 

4

4

4

 

 

 

 

 

 

 

 

 

5

 

2

1

 

 

-1

-2

-3

 

 

 

 

 

 

4

 

 

 

 

125

1

0

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4

 

4

4

 

 

4

4

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

2

3

4

5

6

7

8

9

 

 

 

 

 

 

 

 

 

 

 

 

1

1

1

1

1

1

1

1

1

 

 

 

 

 

 

 

 

 

 

 

1

2

2

1

1

1

0

0

0

0

 

 

 

 

 

 

 

 

 

 

 

1

1

0

2

1

0

4

3

2

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5

 

1

1

 

 

-1

-1

-3

 

 

 

 

 

 

 

 

 

 

 

 

 

1

0

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4

 

 

4

2

4

 

 

 

 

 

 

 

 

 

 

 

 

 

2

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

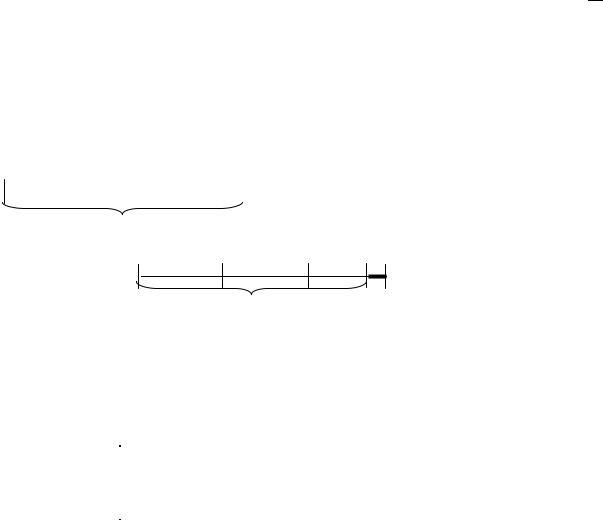
Значение целевой функции уменьшилось наf =ε[6] θ =3 25 =75

Начинаем новую итерацию и проверяем решение на оптимальность

140

maxε[ j]=ε[1]=5/4

 

 

 

 

 

 

1

 

2

3

 

4

 

5 6

7

 

8

 

 

9

 

 

 

 

 

 

 

 

 

1

0

 

 

2

2

 

 

 

 

 

 

 

1

1

1

1

1

1

1

 

1

 

1

 

 

z[N ',1]= B[N ', M ] A[M ,1]

=

 

 

 

 

=

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0

1/ 4

 

 

 

1

1/ 4

 

 

5

 

1

 

 

 

 

 

 

2

1

 

1

1

0

0

 

0

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

100

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

125

1

 

 

1/4

 

 

 

5/4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

2

 

 

1

 

 

 

3

 

2

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

6

 

1

25

 

 

0

 

 

 

0

1

 

 

 

 

 

 

 

 

5

100

1

 

 

0

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4

 

 

4

 

 

4

 

4

 

4

 

 

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

125

5

 

 

1

2

 

 

1

 

0

0

-1

-2

 

-3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

6

25

0

 

 

1/4

 

 

 

1/4

 

 

 

 

 

 

 

4

 

 

4

 

 

4

 

4

 

4

 

 

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Выбор направления и улучшение решения

 

x[i]

 

100

 

25

 

 

 

 

 

 

 

 

θ = min

 

 

 

z[i,1]>0

= min

 

,

 

 

 

=50

=

 

i,1

2

1/4

z

 

 

 

 

 

 

 

[

]

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x[5]

z[5,1]

(Переменная x[5] становится небазисной, а вместо нее базисной становится переменная x[1])

 

 

 

 

 

 

1

2

 

3

 

 

4

 

 

5

 

 

6

7

 

 

8

 

 

9

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

1

 

1

 

1

 

1

 

1

1

 

1

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

1

50

 

1

1

 

1

 

 

1

 

 

1

 

 

0

0

 

0

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

2

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

25

 

 

 

-1

3

 

 

1

 

 

-1

 

 

3

 

 

2

 

 

1

 

 

6

1

 

 

0

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

4

 

 

 

 

 

8

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

8

 

 

8

 

 

 

4

 

 

4

 

 

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

125

 

 

 

-1

-1

-3

 

-5

 

 

-1

-2

 

-3

 

 

 

 

 

 

 

0

 

4

 

 

8

 

 

8

 

 

8

 

0

 

4

 

 

4

 

 

4

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

125

 

 

 

3

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

8

 

 

 

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

50

 

 

 

1

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

6

 

 

 

 

25

 

 

 

 

-1

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

8

 

 

 

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

2

 

 

3

 

 

4

5

 

6

7

 

8

 

9

 

 

 

 

 

1

 

1

 

 

1

 

 

 

1

 

1

 

1

 

1

 

1

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

2

 

 

1

 

 

 

1

 

1

 

0

 

0

 

0

 

0

 

 

8

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

0

 

 

2

 

 

 

1

 

0

 

4

 

3

 

2

 

1

 

 

8

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

-2

 

 

-1

 

 

-3

 

-5

 

 

 

-2

 

-4

 

-6

 

 

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

8

 

 

8

 

 

 

8

 

8

 

 

8

 

8

 

8

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

На новой итерации проверяем решение на оптимальность. Критерий оптимальности выполняется, т. к. все оценки неположительные.

Текущее решение оптимально

N ' = 1,6 .

x 1 =50,

 

x

6

]

=

25

,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

{

}

[ ]

 

 

[

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

{

 

 

 

}

 

 

 

 

[

 

 

]

 

 

 

[

 

 

]

 

 

N \ N ' =

 

 

 

,

x

N \

=0

N \ N '

 

 

2,3,4,5,6,7,8,9

 

 

 

N '

 

 

 

 

 

 

 

2

 

 

25

0

100

 

 

 

 

 

25

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

+

 

 

 

 

 

 

 

 

,

fmin

=1 50+1 =62,5

A[M, N '] x[N ']=50

1

 

 

 

2

 

 

4

=

 

 

 

 

 

 

 

 

 

 

 

 

 

100

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Требуемая память и число итераций

(m =2,n =9)

3 2+2 9+2 9+1=35 чисел.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

35+4 =39 чисел
б) r =(1,2.75)
в) r =(4,−2)

 

141

(4 2+1)(9+1)=90 арифметических

90−[50−26]=66 арифметических

операций

операций

(2+1)(9+1)=30 операций присваивания

30−[18−8]=20 операций присваивания

Задача линейного программирования (*) называется задачей линейного раскроя. Дадим ее постановку на рассмотренном примере.

Итак, имеется одномерное сырье (прутья, бревна, брусья, проволока и т. д.) длиной L =17 единиц, которое необходимо разрезать на заготовки двух типов с длинами 6 единиц и 4 единицы. (l =(6,4) - вектор длин заготовок). Заготовок длины 6 требуется нарезать 100

штук, и столько же требуется заготовок длины 4. Вектор b =(100,100) - вектор требований на заготовки. Назовем способом раскроя неотрицательный целочисленный вектор r =(r1,r2 ), удовлетворяющий условию

 

 

 

 

 

 

l r =6 r1 +2 r2 ≤ L =17. (*)

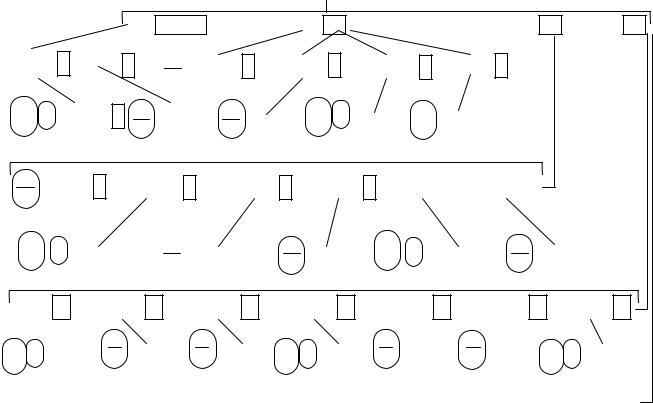
Так вектор r =(2,1)

является способом раскроя

6

 

6

 

4

 

1

 

Вырезается 2 заготовки длины 6 ед. и одна –

 

 

 

 

 

 

 

 

 

 

 

 

длины – 4 ед. Отход – 1 ед.

 

 

 

 

 

 

 

 

 

17

 

 

 

 

Напротив, нижеперечисленные вектора таковыми не являются.

 

а) r =(3,0)

6

6

6

1

(нарушено условие (*))

17 (не является целочисленным)

(нарушена неотрицательность)

Перечислим, пользуясь (*) все возможные способы раскроя, располагая их столбцами матрицы раскроев в порядке лексикографического убывания (убывания старших компонент).

 

1

2

3

4

5

6

7

8

9

 

 

2

2

1

 

1

1

 

0

0

0

0

 

A =

 

 

 

 

 

 

 

 

 

 

 

 

1

0

2

 

1

0

 

4

3

2

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(1)

(5)

(3)

(7)

(11)

(1)

(5)

(9)

(13)

 

(в скобках под каждым столбцом указан отход сырья в данном способе раскроя)

Введем в качестве неизвестных

интенсивности использования способов раскроя ( xi -

сколько раз применяется раскрой с номером

i ), и потребуем минимизации числа штук

сырья используемого на вырезание всех требуемых заготовок (очевидно, что на однократное применение любого способа раскроя расходуется одна штука сырья). Тогда функция цели

f = x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8 + x9 → min

будет выражать суммарную интенсивность (суммарное количество штук израсходованного сырья).

А система ограничений

2

x

+

2

x

+ 1

x

+ 1

x

 

+ 1

x

+

0

x

+ 0

x

+ 0

x

+ 0

x

= 100

 

1

 

1

 

0

 

2

 

2

 

3

 

 

 

4

 

0

 

5

 

4

 

6

 

3

 

7

 

2

 

8

 

1

 

9

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

100

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

обеспечивает выполнение требований на заготовки каждого типа.

142

Добавляя ограничения неотрицательности

 

 

 

 

 

 

 

xi ≥0, (i 1: 9),

 

 

 

 

приходим к задаче линейного программирования

 

 

 

 

 

f = x1 + x2

+ x3 + x4 + x5

+ x6

+ x7

+ x8

+ x9 → min

2x

+2x

+ x

 

+ x

+ x

+ x

 

 

 

 

 

=100

 

1

2

 

3

 

4

 

5

 

 

6

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x1

 

+2x3

+ x4

 

 

+4x6 +3x7 + 2x8

+ x9 =100

 

 

 

 

 

 

 

xi

≥0

 

(i 1:9)

 

 

 

 

Оптимальное решение этой задачи, полученное выше

 

 

 

 

 

 

 

2

 

25

 

0

100

 

 

 

125

 

 

 

 

50

 

 

+

 

 

 

=

 

 

, f

 

=

 

 

,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

min

 

2

 

 

 

 

1

 

 

 

4

 

100

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

можно интерпретировать следующим образом: Для вырезания двух комплектов вектора требований (по сто штук заготовок длины 6 и 4 ед. в каждом) надо 100 раз применить раскрой (2, 1) и 25 раз – раскрой (0, 4). При этом будет израсходовано минимальное количество сырья (125 шт. по 17 ед.).

Легко показать, что минимальное число штук израсходованного сырья соответствует наименьшим возможным отходам сырья .

Задачи раскроя материалов возникают при разрезании одномерного сырья на заготовки (линейный раскрой), плоского сырья на прямоугольные и фигурные заготовки (гильотинный и фигурный плоский раскрой, продольная распиловка древесины и т. п.). Нетрудно заметить, что задачи заполнения фиксированной области (линейной, плоской или объемной) элементами различных конфигураций с заданным их общим числом, при минимизации общего числа использованных областей также является задачей раскройного типа. Например, загрузка в вагоны партии продукции (ящики, рулоны) с заданным объемом партии по каждому виду продукции при минимизации общего числа использованных вагонов.

143

7.13. Задачи раскроя

7.13.1. Постановка задачи

Имеется сырье длины L , которое необходимо раскраивать на заготовки M различных типов ( M =m ). Длины заготовок задаются вектором l[M ], а количество заготовок

каждого типа, которое необходимо нарезать – вектором требований b[M ].

Пусть A[M, N ] - целочисленная неотрицательная матрица всех возможных способов раскроя одной единицы сырья, N = n - число таких способов. Способ раскроя – это столбец матрицы A[M, j], (j 1: N), удовлетворяющий условию:

l[M ] A[M, j]≤ L

Пусть x[N ] - вектор интенсивностей использования раскроев. Тогда задача минимизации

суммарных отходов сырья при условии нарезания всех требуемых заготовок запишется в виде следующей ЗЛП:

f =1[N ] x[N ]→ min A[M, N ] x[N ]=b[M ] x[N ]≥0[N]

Одной из особенностей этой задачи является значительная «ширина» матрицы раскроев

[

]

даже при небольшом числе типов заготовок

m .

 

A M, N

 

 

 

 

 

 

 

 

=3, l =(9,5,3)

 

Так, например, для

L =35 , m =

 

M

матрица всех возможных способов

раскроя содержит 102 столбца (

 

N

 

= n =102)

 

 

 

 

 

 

 

 

 

 

1

2

3

4

5

6

7

8

9 101112 1314 1516 17 1819 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50

 

 

33333222222222 22 2 22 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1

A[M , N ]= 11000322211111 00 00 0 0 5 4 4 4 3 3 3 3 2 2 2 2 2 2 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1021002104 321 054 321 0 0 2 1 0 3 2 1 0 5 4 3 2 1 0 7 6 5 4 3 2 1 0 8 7 6 5 4 3 2 1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80

81 82 83 84 85 86 87 88 89 90 91 92

93 94 95 96 97 98 99 100 101102

1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

0 7 6 6 5 5 5 5 4 4 4 4 4 4 3 3 3 3 3 3 3 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0

0 0 1 0 3 2 1 0 5 4 3 2 1 0 6 5 4 3 2 1 0 8 7 6 5 4 3 2 1 0109 8 7 6 5 4 3 2 1 011109 8 7 6 5 4 3 2 1

Число n быстро растет с ростом числа типов заготовок m , минимальной и максимальной кратностей заготовок в раскрое min(max) L /l[i] ([i] - целая часть числа). Так при m =30

и mini L/l[i] =3, maxi L /l[i] =20 число способов раскроя достигает величины порядка

107 . Естественно, хранить и обрабатывать такую матрицу весьма проблематично. Правда, если избавиться от хранения матрицы раскроев и решить проблему получения (генерации) способа раскроя, вводимого в базис, то становится возможной реализация симплексметода именно модифицированным алгоритмом (обрабатываемая информация имеет порядок m2 , а не m n , как в прямом симплекс-алгоритме).

В задаче линейного раскроя проблема генерации столбца матрицы способов раскроя может быть сведена к решению вспомогательной экстремальной задачи по той простой причине, что способы раскроя – это все целочисленные, неотрицательные векторы r[M ],

удовлетворяющие условию

l[M ] r[M ]≤L (*)

В базис могут вводиться способы раскроя A[M, j] с положительной оценкой

144

ε[ j]= v[M ] A[M, j]−1>0

Поэтому, если отыскать максимум скалярного произведения g =v[M ] r[M ]

при ограничении (*), то при g ≤1 убеждаемся в оптимальности текущего базисного решения, а при g >1 вектор r[M ] будет представлять один из столбцов матрицы

способов раскроя A[M, j0 ], который необходимо ввести в базис. Таким образом, приходим к следующей задаче оптимизации

g =v[M ] r[M ]→ max l[M ] r[M ]≤L

r[M ]≥0[M ], r[M ]−целочисленный

Эта задача линейного целочисленного программирования с одним ограничением задачи о рюкзаке (ранце). Будем называть ее здесь r -задачей (раскрой, рюкзак).

Следуя [9], рассмотрим два подхода к решению этой дискретной экстремальной задачи

7.13.2. Генерирование способа раскроя. Метод ветвей и границ.

По словам И.В.Р.1 все методы решения дискретных задач, оп сути дела, представляют собой улучшенный перебор допустимых решений. Большая группа методов улучшенного перебора объединяется под названием «метод ветвей и границ». Общая идея этого метода для задачи

f (x)→ max, x A

такова:

Пусть имеется некоторое разбиение множества A

A: A = A0 A1 ... Ak

и известно, что в множестве A0 оптимальных решений быть не может. Тогда max{f (x) x A}= max{max{f (x) x Ai }i 1: k}

Выделение множества A0 сокращает задачу, при передаче большей части множества A в A0 , а разбиение оставшейся части A на подмножества Ai может упростить нахождение максимума f (x) (если выбирать такие разбиения при которых эта задача упрощается).

Имеется два важных способа увеличения множества A0 :

1) Если для двух элементов разбиение Ai и Aj

max{f (x) x Aj }<max{f (x) x Ai }, то в Aj нет оптимальных решений и A0 := A0 Aj

2) Если для некоторого допустимого решения x0 и для некоторого элемента разбиения Aj

max{f (x) x Aj }< f (x0 ), то в Aj нет оптимальных решений и A0 := A0 Aj .

Далее, имея некоторое разбиение A можно проводить его дальнейшее измельчение, в котором тот или иной элемент разбиения заменяется его разбиением (несколькими элементами). При этом последовательно уточняются оценки максимума и находятся новые допустимые решения, и некоторые элементы разбиения пополняют собой множество A0 . Рассмотрим реализацию этих принципов в задаче о наилучшем раскрое (r -задаче).

1 Романовский Иосиф Владимирович

145

Приведем пример из [9, с. 230] с сохранением структуры записи о состоянии процесса и обозначений.

l0 =100 - длина сырья M ={1:5}

l[1: 5]=40,9,21,37,20 - длины заготовок v[1: 5]=45,10,23,40,20 - «цены» заготовок

v /l[1: 5]=1.25,1.11,1.095,1.081,1.000 - удельная доходность

r[1: 5] - способ раскроя

γ =v[M ] r[M ] - накопленная выручка

λ - остаток сырья

est - оценка максимума

k - номер последней включенной в решение заготовки rec - рекордное значение целевой функции

 

 

 

r[M ]

 

 

γ

λ

est

k

rec

Оценка остатка на

 

 

 

 

 

 

 

1

2

3

4

5

 

 

 

 

 

первом шаге

1

0

0

0

0

0

0

100

112.5

 

 

100×45/40 =112.5

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Первых заготовок может уместиться не более двух. Отрезаем две первых заготовки. Получаем выручку 90 и остаток 20.

 

 

2

 

2

 

0

 

 

0

 

 

0

 

 

0

 

 

 

90

 

 

 

20

 

 

 

112.222

 

1

 

 

90

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Оценка

 

остатка 20×10/9 =22.222 . Оценка

 

 

способа

раскроя

должна

учитывать

накопленную выручку

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

90+22.222 =112.222

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Вторых деталей в остаток можно уместить две

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

2

 

 

2

 

0

 

 

 

0

 

 

0

 

 

 

110

 

2

 

0

 

 

 

2

 

110

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

по загот. 2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(0)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

111.111

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(2)

112.222

 

 

(1)

 

111.667

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

R1

110

(2,2)

(2,1)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

×

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

110

(2,0,0,0,1)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

×

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

105

(1,6)

 

95

(1,5)

 

(1,4)

111.286

 

 

(1,3)

111.143

 

 

(1,2)

 

111

 

(1,1)

110.857

 

 

 

 

×

 

108

 

(1,41)

 

 

 

 

98

(1,3,1)

 

R2

111

(1,2,2)

 

 

 

 

 

 

 

 

×

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

×

 

 

 

 

 

 

 

×

 

 

 

 

 

 

 

 

 

×

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

110

 

(0,11)

 

 

100

(0,10)

 

 

90

 

(0,9)

 

 

 

(0,8)

 

109.571

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

×

 

 

 

 

 

 

×

 

 

 

 

 

 

 

×

 

 

 

 

 

 

 

×

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Накопленное решение (2,2), выручка 110, остаток 2. Из остатка ничего вырезать нельзя. Делаем шаг назад, отказавшись от одного экземпляра второй заготовки. Накопленное решение (2,1), выручка 100, остаток 12. Из этого остатка вырезать ничего нельзя. Шаг назад.

146

Накопленное решение (2,0), выручка 90, остаток 20. Из остатка вырезается заготовка 5, что дает оценку и значение целевой функции 110. Так как, решение с таким значением уже имеется, следует сделать первый шаг назад.

Накопленное решение (1), выручка 45, остаток 60. Оценка варианта 45+60+1.11=111.667 .

Накопленное решение (1,6), выручка 105, остаток 6. (105<110) Шаг назад: (1,5), 95, 15.

Шаг назад: (1,4), 85, 24. Оценка варианта 85+24×23/21=111.286 Шаг вперед: (1,4,1), 108, 3 (108<110)

Шаг назад: (1,4,0), оценка 109 (по заготовке 5) (109<110) Шаг назад: (1,3), 75, 33, оценка 111.143 (по заготовке 3) Шаг вперед: (1,3,1), 98, 12 (98<110)

Шаг назад: (1,3,0), 75, 33 оценка 108 (на заготовке 5) (108<110) Шаг назад: (1,2), 65, 42, оценка 111 (по заготовке 3)

Шаг вперед: (1,2,2), 111, 0 – это новый рекорд!

Шаг назад: (1,1), 55, 51, оценка 110, 857 (по заготовке 3) (110, 857<111) Шаг назад: (0), 0, 100, оценка 111.111 (по заготовке 2)

Шаг вперед: (0,11), 110, 1 (110<111) Шаг назад: (0,10), 100, 10 (100<111) Шаг назад: (0,9), 90, 19 (99<111)

Шаг назад: (0,8), 80, 28, оценка 109, 571 (по заготовке 3) (109, 571<111) Шаг назад: (0,7), 70, 37, оценка 70+37×23/21=110.524 (110.524<111) Шаг назад: (0,6), 60, 46, оценка 60+46×23/21

. . .

Шаг назад: (0,0) оценка 100×23/21=109.5 (по заготовке 3)<111

Ветвь запрещается. Перебор заканчивается. Единственный рекорд R2 =111 соответствует способу раскроя (1, 2, 2) с нулевым отходом.

В следующем примере ( L =35, l =9,5,3, v =9/35, 5/35, 3/35 ), дерево которого показано на рисунке ниже, рекордных записей семь.

(0)

 

 

 

 

 

 

(3)

35/35

 

 

 

(2)

 

1

 

 

 

 

 

(1)

1

(0)

1

(3,1)

1

(3,0)

1

33

 

(2,3)

1

(2,2)

 

1

 

(2,1)

1

 

(2,0)

1

 

 

 

 

 

 

 

 

 

 

35

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

R

1 (3,1,1)

1 33

3,0,2

 

34

2,2,2

R

1(2,1,4)

33 (2,0,5)

 

 

 

 

1

 

 

 

 

 

35

 

 

 

35

 

 

 

2

 

 

 

35

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

×

 

 

 

×

 

 

 

 

 

 

 

×

 

 

 

 

34

(1,5)

1

 

(1,4)

1

 

(1,3)

1

 

(1,2)

1

(1,1)

 

1

(1,0)

1

 

 

35

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

×

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

R

1

(1,4,2)

 

33

 

(1,3,3)

 

34

1,2,5

 

R

1 (1,1,7)

33

1,0,8

 

 

3

 

 

 

 

 

35

 

 

 

 

35

 

 

 

4

 

 

 

35

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

×

 

 

 

 

×

 

 

 

 

 

 

 

 

×

 

(0,7)

1

 

 

(0,6)

1

 

(0,5)

1

 

(0,4)

1

 

(0,3)

1

 

(0,2)

1

(0,1)

1

 

 

 

 

 

33

 

 

 

34

 

 

 

 

 

 

 

33

 

 

34

 

 

 

 

R

1

(0,7,0)

 

35

(0,6,1)

 

35

(0,5,3)

R

1

(0,4,5)

 

35

(0,3,6)

35

(0,2,8)

R

1 (0,1,10)

5

 

 

 

 

 

 

 

 

 

6

 

 

 

 

 

 

 

7

 

 

×

×

×

×

×

×

×

147

Ниже приводится текст процедуры с комментариями

bestsol[N]=0[N]; x[N]=0[N]; k=0; lam=l0; gam=0; rec=0;

{начальные установки}

mkest: if k=m then goto mkback else k:=k+1; if l[k]> lam then goto mkest;

{ищем номер детали, которую можно вырезать из остатка lam. Если длины всех деталей больше остатка (k=m), делаем шаг назад (mkback)}

est:=gam+lam*c[k]/l[k];

{вычисляем оценку продолжения = доход + оценка остатка} if est<=rec then goto mkback;

{Если продолжение неперспективно, то делаем шаг назад (mkback)}

x[k]:=entire(lam/l[k]); lam:=lam-x[k]*l[k]; gam:=gam+x[k]*c[k];

{шаг вперед: Вырезаем из остатка максимальное число деталей с номером k. Уменьшаем остаток на вырезанную длину. Увеличиваем доход на добавившуюся стоимость.} if rec<gam then begin rec:=gam;

for I:=1 step 1 until m do bestsol[i]:=x[i] end;

{Если доход рекордный, делаем его текущим рекордом,

а соответствующий способ раскроя записываем в bestsol} goto mkest;

{Если доход меньше рекорда, пытаемся отыскать новый способ раскроя, шагая вперед}

mkback: k:=k-1;

{шаг назад: Выбираем номер предыдущей заготовки} if x[k]>0 then

begin x[k]:=x[k]-1; lam:=lam+l[k]; gam:=gam-c[k]; goto mkest end;

{Если она вырезалась, то уменьшаем её количество на единицу, остаток увеличиваем на ее длину, а доход уменьшаем не её цену. Далее пытаемся найти продолжение, шагая вперед}

else if k>1 then goto mkback;

{Если она не вырезалась (x[k]=0), то идем к предыдущей заготовке. Если ни одна заготовка не вырезана – на способе раскроя (0,0,…,0) процедура заканчивает работу

с результатом: bestsol[N]– наилучший способ раскроя; rec – рекордно максимальное значение дохода c[N]*bestsol[N]}

148

7.13.3 Генерирование способа раскроя. Способ, основанный на решении функционального уравнения Беллмана (уравнения динамического программирования)

Будем считать длину сырья L и длины заготовок l[M ] целыми числами (это позволит в

дальнейшем ограничиться конечным множеством длин текущего сырья). Кроме того, добавим в M заготовку длины 1 с нулевым доходом. Рассмотрим граф M, N ,

N =

{

u

}

сопоставим множество

 

u 0: L,u - целое . Каждой вершине этого графа i M

деталей Ni , которые можно отрезать от текущего сырья длины i .

Ni ={j 0: n l[ j]≤i},

j сопоставим дугу, ведущую из i в вершину i−l[ j], приносящую доход v[j] (заметим,

что из каждой вершины i 1: L , можно перейти в i−1 с нулевым отходом). Исходная задача о наилучшем раскрое эквивалентна задаче о нахождении пути наибольшей длины из L в в построенном графе. Действительно, каждый такой путь можно интерпретировать как последовательность заготовок, отрезаемых от всей длины сырья. С другой стороны, каждому раскрою – набору отрезаемых заготовок – можно сопоставить (не единственным образом) последовательность, в которой эти заготовки отрезаются и,

следовательно,

путь

 

от

вершины

L

 

 

до вершины в графе

 

 

M, N .

 

Для

L =10, l =6,5,3, v = 2, 3, 2 граф

M, N

 

представлен на рис. ниже.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

10

0

 

 

9

0

 

8

 

 

 

0

 

7

 

0

 

6

 

 

 

 

0

 

5

0

 

4

0

3

0

2

 

0

 

 

1

 

 

 

 

 

 

0

 

 

 

2

 

 

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Выделены два пути максимальной длины 6. В примере L =13, l =4,3,2, v =

4

,

 

3

,

 

2

;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

13

 

 

13

 

13

1 2 3 4 5 6 7 8 9 10 1112

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3 2 2 1 1 1 1 0 0

0

0

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0 1 0 3 2 1 0 4 3

2

1

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0 1 2 0 1 3 4 0 2

3

5

6

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(1) (0) (1) (0) (1) (0) (1) (1) (0) (1) (0) (1)

число раскроев с максимальным доходом 1 равно 5. (выделены в таблице способов раскроя). Каждому из них единственным образом сопоставлен путь в приведенном на рис. графа. Так способу раскроя номер 2 (2, 1, 1) в графе сопоставлено 12 путей, три из которых выделены. А способу раскроя с номером 1 (3, 0, 0) соответствуют 2 пути в графе.

1312840

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности