
Задачи ЛП и методы их решения
.pdf
|
|
|
|
|
120 |
|
|
Примеры |
|
|
|
|
|
|
|
1 а) |
|
|
|
|
|
|
|
|
( I ) |
f |
= x1 + 2x2 |
→ max |
( II ) |
g = 6y1 |
+10y2 → min |
|
|
|
3x1 + x2 = 6 |
|
3y1 + 6y2 =1 |
||
|
|
6x1 + 2x2 =10 |
|
y1 + 2y2 = 2 |
|||
|
Множество допустимых |
|
Множество допустимых |
||||
|
решений |
D = , т.к. при |
|
решений |
E = . Система |
||
|
умножении 1-го уравнения на 2- |
|
уравнений несовместна |
||||
|
получим |
6x1 + 2x2 |
=10. Система |
|
|
|
|
|
уравнений несовместна. |
|
|
|
|||
1 б) |
|
|
|
|
|
|
|
|
( I ) |
f |
= x1 + 2x2 |
→ max |
( II ) |
g = 6y1 |
+10y2 → min |
|
|
|
3x1 + x2 = 6 |
|
3y1 + 6y2 ≥1 |
||
|
|
6x1 + 2x2 =10 |
|
y1 + 2y2 ≥ 2 |
|||
|
|
x1 ≥ 0 , x2 ≥ 0 |
|
|
|
||
. |
D = |
E |
= {(y1 , y2 ) : y1 + 2y2 ≥ 2} - полуплоскость |
||||
|
|
|
|||||
|
|
|
|
x1 |
|
|
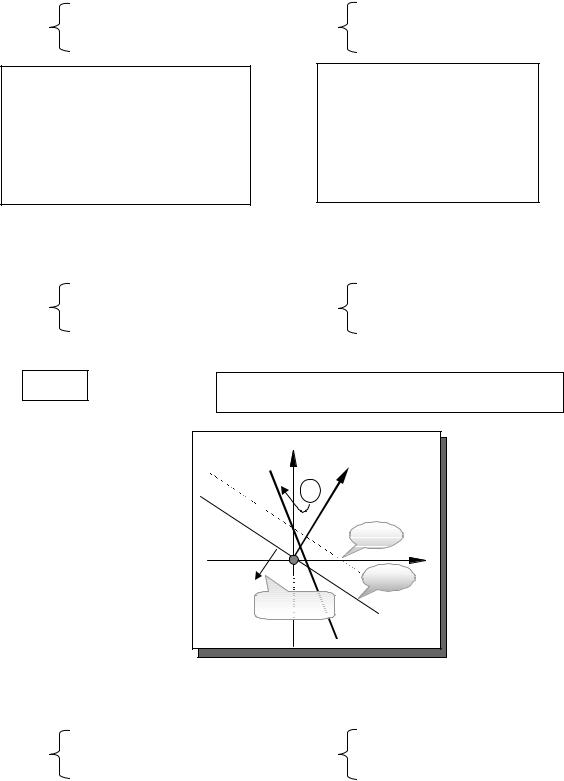
Целевая функция g |
|
|
|
|
|
|
не ограничена на |
|
|
|
|
|
|
y2 |
N (6,10) |
|
|
|
|
|
|
E |
|
множестве решений |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g=20 |
y1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
g=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g → −∞ |
|
|
2 |
|
|
|
|
|
|
|
|
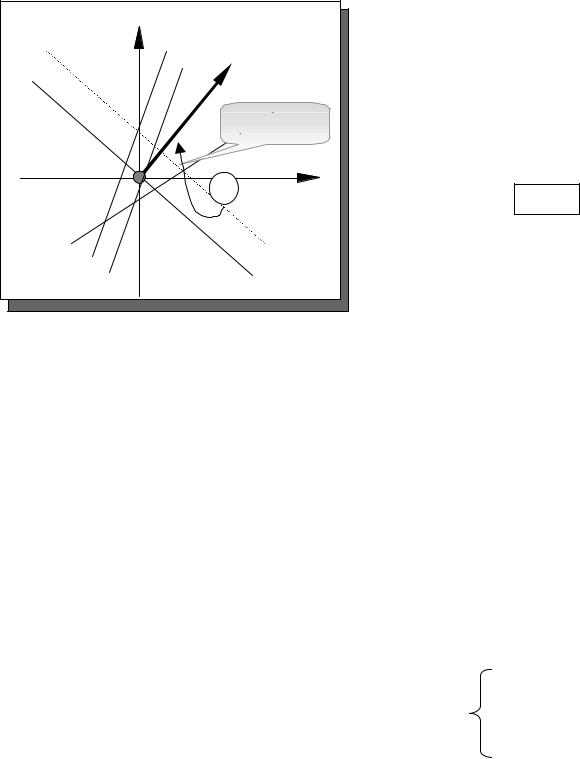
( I ) |
f |
= x1 + x2 → max |
( II ) |
g = 2y1 |
+ 2y2 → min |
|
|
|
|
− 2x1 + x2 ≤ 2 |
|
− 2y1 + y2 =1 |
||
|
|
|
x1 − 2x2 ≤ 2 |
|
y1 − 2y2 =1 |
||
|
|
|
|
|
|
y1 ≥ 0 , y2 ≥ 0 |
|
122
условий дополняющей нежесткости и позволяют по оптимальному решению одной из пары двойственных задач найти оптимальное решение другой.
Теорема 5 ( 2-я теорема двойственности) |
|
|
X 0 [N],Y0[M ] - оптимальные решения |
а) (A[i, N] X 0 [N] − b[i]) y0 [i] = 0, |
i M |
задач (I) и (II) соответственно |
б) (Y0[M ] A[M, j] − c[ j]) x0 [ j] = 0, |
j N |
условия дополняющей нежесткости
Доказательство
а)
f (X0 ) = C[N] X0[N] ≤ (т.к. C[N] ≤ Y0[M ] A[M , N])≤ Y0[M ] A[M , N] X0[N] ≤ (т.к. A[M , N] X0[N] ≤ b[M ])≤ Y0[M ] b[M ] = g(Y0 )
б)
Но по условию теоремы f (X 0 ) = g(Y0 ), т.к. X 0 ,Y0 - оптимальные решения. Тогда в цепочке
преобразований везде должен стоять знак равенства. В соответствии с выделенным, получаем
а) Y0 [M ] A[M , N] X 0 [N] = Y0 [M ] b[M ] Y0 [M ] (A[M, N] X 0[N] − b[M ])= 0 б) C[N] X 0 [N] = Y0[M ] A[M, N] X 0[N] (Y0 [M ] A[M, N] − b[M ]) X 0 [N] = 0 Скалярная запись условий а) и б) следует из того, что оценки (выражения в скобках) равны нулю для базисных переменных, а если оценки отличны от нуля, то соответствующие им
переменные являются небазисными (т.е. равны нулю).
В этом случае X 0 [N],Y0 [M ] - допустимые решения ЗЛП (I) и ЗЛП (II) соответственно. Запишем а) и б) в векторном виде
Y0 [M ] (A[M, N] X 0 [N]−b[M ])= 0 Y0 [M ] A[M, N] X 0 [N] = Y0 [M ] b[M ] = g(Y0 ) (Y0[M ] A[M, N] − b[M ]) X 0 [N] = 0 Y0 [M ] A[M , N] X 0 [N] = C[N] X 0 [N] = f (X 0 ) Так как равны левые части двух последних равенств, то равны и правые. Т.е.
f (X 0 ) = g(Y0 )
По 1-й теореме двойственности получаем, что X 0 [N],Y0 [M ], - оптимальные решения прямой
и двойственной ЗЛП соответственно ■ Информативным прочтением условий дополняющей нежесткости является следующее:
1) если переменная в исходной задаче y0 [i],(x0 [ j]) отлична от нуля, то соответствующее ей ограничение в двойственной выполняется как равенство
A[i, N] X 0 [N] = b[i] (Y0 [M ] A[M , j] = c[ j])
2) если ограничение в исходной задаче выполняется как строгое неравенство A[i, N] X 0 [N] < b[i] (Y0 [M ] A[M, j] > c[ j])
то соответствующая ей переменная в двойственной задаче y0 [i],(x0 [ j]) равна нулю.
hЗаметим, что при равенстве нулю одного из сомножителей в условиях дополняющей нежесткости о величине второго сомножителя ничего сказать нельзяh
Примеры
Сначала поясним до конца пример 1 (см. также замечание после примеров к постановке двойственных задач)

123
( I ) |
f = 7x1 |
+ 3x2 − x3 |
+ 2x4 → max |
( II ) |
g = 9y1 + 7y2 → min |
|
|||||
|
2x1 + x2 + 4x3 − x4 ≤ 9 |
|
2y1 + y2 = 7 |
|
|||||||
|
x + x |
2 |
− x |
3 |
+ x |
4 |
= 7 |
|
y1 + y2 ≥ 3 |
|
|
|
1 |
|
|
|
|
|
|
|
|||
|
x2 ≥ 0, x4 ≥ 0 |
|
|
4y1 − y2 = −1 |
|
||||||
|
|
|
|
|
|
|
|
|
|
− y1 + y2 ≥ 2 |
|
|
|
|
|
|
|
|
|
|
|
y1 ≥ 0 |
|
Находим решение ЗЛП (II): |
|
|
|
|
|
||||||
2y1 + y2 |
= 7 |
|
y1 |
=1; |
y1 + y2 =1+ 5 = 6 ≥ 3 |
Оптимальное решение ЗЛП (II) |
|
||||
4y1 − y2 |
= −1 |
|
y2 = 5 ; − y1 + y2 = −1+ 5 = 4 ≥ 2 |
y1 |
=1, y2 = 5, gmin = 9 1+ 7 5 = 44 |
||||||
|
|
|
y1 =1≥ 0 |
|
|
|
|
||||
Из условий дополняющей нежесткости имеем |
|
|
|
||||||||
а) y1 (2x1 + x2 + 4x3 − x4 − 9) = 0 т. к. y1 > 0 , то |
|
2x1 + x2 + 4x3 − x4 = 9 |
|
||||||||
y2 (x1 + x2 − x3 + x4 − 7) = 0 т. к. y2 > 0 , то |
|
x1 + x2 − x3 + x4 = 7 |
( * ) |
||||||||
б) (y1 + y2 − 3) x2 = 0 т. к. |
|
y1 + y2 =1+ 5 > 3 , то x2 = 0 |
|
|
|||||||
(−y1 + y2 − 2) x4 = 0 т. к. − y1 + y2 = −1+ 5 > 2 , то x4 = 0 |
|
|
|||||||||
Подставляя x2 = 0 и x4 |
= 0 в систему уравнений (*) имеем |
|
|
||||||||
2x1 + 4x3 = 9 |
|
|
|
x3 |
= −5 6, x1 = 37 6, |
fmax = 7 37 6 + 5 6 = 44 |
|
||||
x1 − x3 = 7 |
|
|
|
|
|
Оптимальное решение ЗЛП (I) |
|
||||
6
( I ) f = 4x1 + 6x2 + 5x3 + 5x4 + 2x5 → min |
( II ) g =12y1 + 8y2 → max |
||||||||||||
x1 + 3x2 + x3 + 5x4 − x5 =12 |
y1 + 2y2 |
≤ 4 |
|||||||||||
2x + x |
2 |
+ x |
3 |
+ x |
4 |
+ x |
5 |
= 8 |
3y1 |
+ y2 |
≤ 6 |
||
1 |
|
|
|
|
|
|
|
|
|
||||
x |
i |
≥ 0, i 1:5 |
|
|
|
y1 + y2 |
≤ 5 |
||||||
|
|
|
|
|
|
|
|
|
|
5y1 |
+ y2 |
≤ 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
− y1 |
+ y2 ≤ 2 |
|
Решим задачу (II) графическим способом |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Y * : |
y |
1 |
+ 2y |
2 |
≤ 4 |
y |
2 |
= 5 3 |
||
x1 |
|
|
опт |
|
|
|
|
|
|
||||
|
|
|
5y |
|
+ y |
|
≤ 5 |
|
y |
= 2 3 |
|||
y2 |
|
(V) |
|
1 |
2 |
|
|||||||
|
5 |
|
|
|
|
|
|
|
|
|
1 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(I) |
|
|
|
|
|
|
= 12 2 3 |
+ 8 5 3 = 64 3 |
|||||
|
|
N (12,8) |
|
gmax |
|||||||||
|
|
|
|
||||||||||
|
1 |
y1 |
|
|
|
|
|
|
|
|
|
|
|
0 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Для нахождения оптимального решения задачи (I) |
||||||||||||
|
|
(III) |
|||||||||||
|
(II) |
(IV) |
применим условия дополняющей нежесткости в форме б). |
||||||||||
|
|
|
|||||||||||
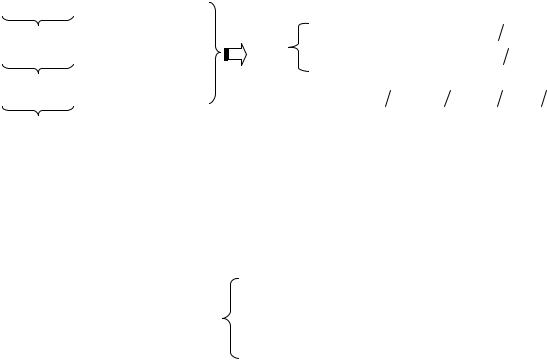
124
Так как 2, 3, 5-е неравенства выполняются как строгие, то имеем
(3y1 + y2 − 6) x2 = 0 x2 = 0 |
|
|
|
|
|
|
|
|
>0 |
X * |
: |
x + 5x |
4 |
= 12 |
x |
4 |
= 16 9 |
|
опт |
|
1 |
|
|
|
||
(y1 + y2 − 5) x3 = 0 x3 = 0 |
|
2x1 + x4 = 8 |
x1 = 28 9 |
|||||
>0 |
|
|
|
|
|
|
|
|
(− y1 + y2 − 2) x5 = 0 |
x5 = 0 |
|
fmin = 4 28 9 + 5 16 9 = 192 9 =64 3 |
|||||
>0 |
|
|
|
|
|
|
|
|
7.11. Матричная транспортная задача (ТЗ)
Закрытая ТЗ формулируется как ЗЛП следующего вида:
m |
n |
f = ∑ ∑c[i, j] x[i, j] →min |
|
i=1 |
j=1 |
n
∑x[i, j] = a[i], i 1: m
j=1
m
∑x[i, j] = b[ j], j 1: n
i=1
x[i, j] ≥ 0 , i 1: m, j 1: n
где
a[i] - запас i-го поставщика
b[ j]- потребность j-го потребителя
c[i, j] - цена перевозки единицы продукции по коммуникациям (i, j) (от i-го поставщика к j-му потребителю)
x[i, j] - объем перевозки продукции (неизвестный) по коммуникации (i, j).
Для вывода критерия оптимальности ТЗ построим двойственную задачу. Структура матрицы системы ограничений ТЗ такова (см.п.4.2.), что столбец, соответствующий переменной
x[i, j] содержит ровно два ненулевых элемента: единицу в строке с номером i и единицу в строке m + i . Вектор двойственных переменных
Y = (u[1], ,u[m] , v[1], ,v[n] )
имеет m + n компонент ( по числу ограничений ТЗ ), которые называются потенциалами: переменные u[1],u[2], ,u[m] - потенциалы поставщиков; переменные v[1],v[2], ,v[n] - потенциалы потребителей.
Используя схему для построения двойственной задачи к ЗЛП в стандартной форме, имеем.
m |
n |
g = ∑a[i] u[i]+∑b[ j] v[ j] → max |
|
i=1 |
j=1 |
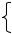 u[i] + v[ j] ≤ c[i, j] , i 1: m , j 1: n
u[i] + v[ j] ≤ c[i, j] , i 1: m , j 1: n
В полученной двойственной задаче m n ограничений, соответствующих каждой переменной x[i, j] ТЗ. Вспоминая, что невязка между левой и правой частью в ограничении двойственной задачи есть оценка для соответствующей переменной исходной задачи (см. подраздел 5.10) запишем условия оптимальности текущего плана перевозок в ТЗ:
ε [i, j] = u[i] + v[ j]− c[i, j] ≤ 0, i 1: m, j 1: n
125
или
u[i]+ v[ j] ≤ c[i, j], i 1: m, j 1: n
Неизвестные потенциалы u[i] и v[ j] (их общее количество равно m + n ) могут быть найдены (и именно так отыскиваются) из условия равенства нулю оценок для базисных переменных (заполненных клеток таблицы) ТЗ (таких равенств (m + n −1), что следует из замечания ниже).
u[i]+ v[ j] ≤ c[i, j] , для заполненных клеток (i , j) таблицы ТЗ.
Решение полученной системы (содержащей неизвестных на единицу больше, чем число уравнений) ищется, когда одно из неизвестных (вообще говоря, любое) полагается равным некоторому числу (тоже, вообще говоря, любому). После этого оставшаяся система имеет единственное решение.
hРанг матрицы системы ограничений ТЗ равен m + n −1. Это следует из того, что при сложении всех строк матрицы, соответствующих первой группе ограничений (см. п.4.2.) получается строка из единиц. Такая же строка получится при сложении всех строк второй группы. Отсюда следует, что нет подматрицы матрицы А порядка m + n с определителем отличным от нуля ( в миноре будет 2 одинаковые строки, что соответствует определителю равному нулю). Тогда
rank A ≤ m + n −1
А подматрицу порядка m + n −1 с определителем отличным от нуля, можно получить взяв из каждой (кроме последней) группы столбцов (см. матрицу в п.4.2.) по одному, а последнюю группу целиком и вычеркнув строку с номером m. Получится квадратная верхняя треугольная матрица порядка m + n −1 с единицами на главной диагонали. Определитель такой матрицы равен 1. Значит
rank A = m + n −1
А если это так, то число базисных компонент в любом базисном решении должно быть равно m + n −1h
Рассмотрим теперь вопрос о разрешимости закрытой ТЗ. Докажем следующее
Утверждение
Закрытая ТЗ всегда разрешима.
Доказательство
Необходимо установить следующее:
а) закрытая ТЗ имеет хотя бы одно допустимое решение б) целевая функция ТЗ ограничена снизу
|
|
a[i] b[ j] |
|
m |
|
|
n |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
а) Проверим, что x[i, j] = |
|
|
|
|
|
|
|
|
|
|
|
|
является допустимым решением |
|||||
|
M |
M |
= ∑a[i] = ∑b[ j] |
|||||||||||||||
|
|
|
i=1 |
|
|
j=1 |
|
|
|
|
|
|
||||||
закрытой ТЗ. Неотрицательность очевидна, т.к. a[i] > 0, b[ j] > 0, M > 0 . |
||||||||||||||||||
Подставим предъявленное решение в произвольное ограничение 1-й группы |
||||||||||||||||||
|
|
n |
n |
|
|
|
|
|
|
|
n |
|
|
|
|
|
||
∑x[i, j] = ∑ |
a[i] b[ j] |
= |
|
a[i] |
∑b[ j] = |
a[i] |
|
M = a[i] |
||||||||||
|
|
|
|
|||||||||||||||
|
j=1 |
j=1 |
M |
|
|
M |
j=1 |
|
|
M |
||||||||
и в ограничения 2-й группы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
m |
m |
|
|
|
|
|
|
|
m |
|
|
|
|
|
|||
∑x[i, j] = ∑ |
a[i] b[ j] |
|
= |
b[ j] |
|
∑a[i] = |
b[ j] |
M = b[ j] |
||||||||||
|
|
|
||||||||||||||||
|
i=1 |
i=1 |
M |
|
|
M |
i=1 |
|
|
M |
||||||||
126
Всем ограничения ТЗ предъявленное решение удовлетворяет, и, следовательно, является допустимым решением ТЗ.
б) Выберем C0 = min{c[i, j], i 1: m, j 1: n}- наименьшую цену перевозки. Заменим в целевой функции ТЗ все коэффициенты на C0 . Тогда получим
m |
n |
m |
|
n |
|
m |
|
|
|
|
|
|
= C0 ∑a[i] = C0 M =ˆ M0 = const |
f = ∑ ∑c[i, j] x[i, j] ≥ C0 ∑ |
∑x[i, j] |
|||||
i=1 |
j=1 |
i=1 |
|
j=1 |
|
i=1 |
Т.е. целевая функция ТЗ ограничена снизу константой M0 . ■
(далее)

|
|
|
|
|
|
|
|
128 |
|
|
|
|
Если хранить и |
перерабатывать |
матрицу z[N ', N ] |
коэффициентов разложения |
|||||||||
столбцов матрицы |
[ |
|
] |
|
|
[ |
|
] |
, то приходим к алгоритму |
|||
A M, N |
|
по текущему базису A M,N ' |
|
|||||||||
прямого симплекс-метода |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
C[N ] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
N ' |
|
C[N '] |
|
x[N '] |
|
z[N ', N ] |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) |
|
ε[N ] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
перерабатываемая информация в симплекс-таблице выделена.
Рассмотрим теперь алгоритм, основанный на использовании вектора двойственных переменных v[M ] при вычислении оценок
ε[ j]= v[M ] A[M, j]−C[ j]
Нетрудно заметить, что оценка в этом случае представляет невязку (разность между левой и правой частью) соответствующего ограничения в двойственной задаче. Этот алгоритм называется модифицированным симплекс-методом и перерабатываемая в нем информация располагается в следующей симплекс–таблице
|
f (x) |
v[M ] |
ε[ j0 ] |
|
|
|
|
N ' |
x[N '] |
B[N ',M ] |
z[N ', j0 ] |
|
|
|
|
дополнительно хранится информация, необходимая при вычислении оценок
|
|
|
C[N ] |
|
|
|
|
|
|
v |
M |
] |
A M, N |
] |
[ |
|
[ |
||
|
|
|
|
|
|
|
|
ε[N ] |
|
|
|
|
|
|
Опишем модифицированный алгоритм по шагам.
Нулевой шаг. Построение начального допустимого базисного решения сводится к нахождению обратной матриц к выбранной базисной матрице A[M,N '], что
эквивалентно решению системы линейных алгебраических уравнений с порядком равным числу ограничений. При этом не гарантируется допустимость получаемого базисного решения. Поэтому, если в матрице системы ограничений ЗЛП, есть единичная (либо диагональная), обратная к которой также единичная (либо диагональная с обратными величинами на диагонали), она и выбирается в качестве начальной базисной.

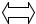 D и E одновременно не пусты.
D и E одновременно не пусты. Пусть
Пусть 
 ЗЛП (I) разрешима (
ЗЛП (I) разрешима (  ЗЛП (II) разрешима (т.к. по теореме 2
ЗЛП (II) разрешима (т.к. по теореме 2