Задачи ЛП и методы их решения
.pdf
99
X = |
1 |
X |
|
+ |
1 |
X |
|
, где X |
|
, X |
|
D ( * ) |
|
1 |
|
2 |
1 |
2 |
|||||||
2 |
|
2 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||
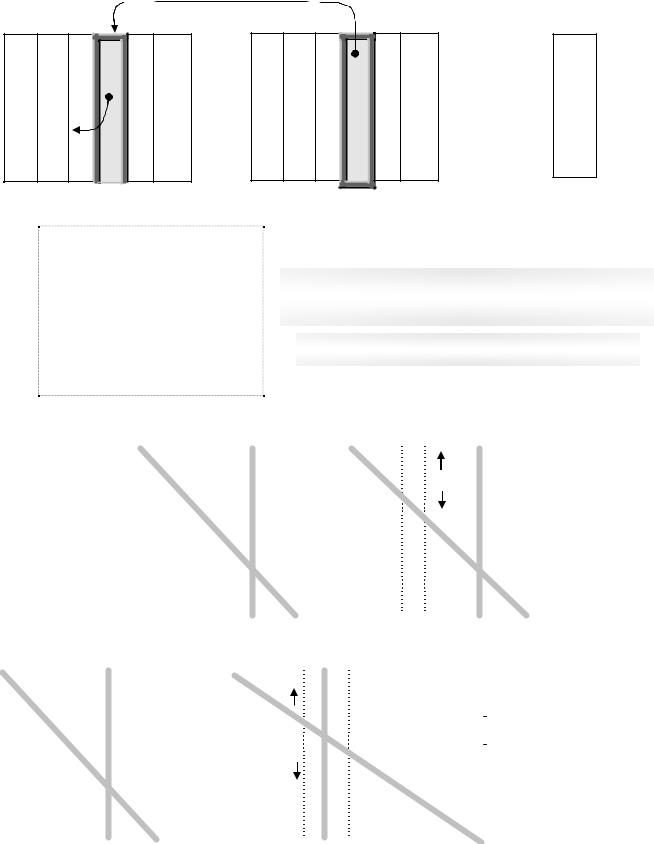
hЛюбую точку выпуклого множества (кроме вершин) можно представить как середину отрезка с концами, лежащими в данном множестве, т.е. в виде (*) (см. рисунок)h
Угловая |
|
|
точка |
|
|
Вершина |
…ЭТО … |
Базисное решение |
|
|
|
X0 |
x0 [N] |
|
|
|
|
Внутренняя |
|
A[M, N] x0 [N]= b[M ] |
точка |
|
|
D |
|
x0 [N]≥ Ο[N] |
Граничная точка |
|
|
7.4. Характеристика угловых точек
Каждое допустимое решение ЗЛП является некоторой точкой множества D (см. (+)). Оказывается вершинам данного выпуклого множества соответствуют базисные решения ЗЛП (см. Рис.)
Утверждение
X 0 [N]- базисное решение ЗЛП
|
|
X 0 [N]-угловая точка множества допустимых решений D |
||||
Доказательство |
|
|
|
|
||
Пусть N ' - базисное множество, соответствующее решению X |
0 |
и |
||||
|
|
|
|
|
|
|
X |
0 |
[N]- невырожденное базисное решение ( X |
0 |
[N ' ] ≥ 0[N ' ]) |
|
|
|
|
|
|
|
||
Не уменьшая общности можно считать, что N ' = {1,2, ,m} (в противном случае можно перенумеровать неизвестные).
(от противного) Пусть X 0 [N] - невырожденное базисное решение и предположим,
что X 0 [N] представимо в виде (*), т.е. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
X1[N], X 2[N] D |
|
|||||||
|
|
|
X[N] = |
|
|
X1[N] + |
|
|
X 2 [N] , где |
|
||||||||||||||
|
|
|
|
2 |
|
|||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Очевидно, что X |
1 |
[N \ N ' ] = X |
2 |
[N |
\ N ' |
] = 0[N \ N ' ] , т.к. в противном случае, |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
i N \ N ' : x |
[i] > 0 . Последнее невозможно в силу того, что X |
0 |
[N \ N ' ] = 0[N \ N ' |
] как |
||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
небазисная часть базисного решения |
|
X 0 [N]. Таким образом, представление для X 0 |
можно |
|||||||||||||||||||||
записать для N ' N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
X[N ' ] = |
1 |
X |
[N |
' ] + |
1 |
X |
|
[N ' ], X |
|
[N'] ≠ X |
|
[N']; |
|
||||||||
|
|
|
|
|
2 |
1 |
2 |
|
||||||||||||||||
|
|
|
|
|
|
|
2 |
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||

100
В силу допустимости решений X1[N] и |
X 2 [N] можно записать. |
|||||||
A[M, N] X |
[N] = A[M, N |
' ] X |
[N ' ] = b[M ] |
|||||
1 |
|
|
|
|
|
1 |
|
|
A[M, N] X |
2 |
[N] = A[M, N |
' ] X |
2 |
[N ' ] = b[M ] |
|||
|
|
|
|
|
|
|
||
Вычитая из первого равенства второе, и используя обозначение |
||||||||
λ[N ' ] = X |
2 |
[N ' ] − X |
1 |
[N ' ] ≠ 0[N ' ] |
||||
|
|
|
|
|
|
|
||
получаем |
|
|
|
|
|
|
|
|
A[M, N ' ] λ[N ' ] = 0[M ] , |
λ[N ' ] ≠ 0[N ' ] !!! |
|||||||
линейную зависимость столбцов матрицы A[M , N ' ] , что противоречит базисности матрицы |
||||||||
A[M , N ' ] . Следовательно, неверным является исходное предположение о представимости |
||||||||
X 0 [N] в виде (*) и, таким образом, X 0 [N] |
является вершиной множества D. |
|||||||
 Пусть теперь X 0 [N] - вершина множества D и предположим, что столбцы матрицы A[M , N ' ] - линейно зависимы, т.е. λ[N ' ] ≠ 0[N ' ]:
Пусть теперь X 0 [N] - вершина множества D и предположим, что столбцы матрицы A[M , N ' ] - линейно зависимы, т.е. λ[N ' ] ≠ 0[N ' ]:
A[M, N ' ] λ[N ' ] = 0[M ] (**) Рассмотрим вектор λ[N] = (λ[N ' ], 0[N \ N ' ]) . Очевидно, что
A[M, N] λ[N] = A[M, N ' ] λ[N ' ] + A[M, N \ N ' ] 0[N \ N ' ] = 0[M ] Возьмем число ε > 0 настолько малым, что неотрицательность векторов
X1[N] = X 0 [N] + ε λ[N] и |
X 2 [N] = X 0 [N] − ε λ[N] будет иметь место (положительные |
||||||||
компоненты вектора могут уменьшится только до нуля). |
|||||||||
Теперь нетрудно убедиться в допустимости решений ЗЛП X1[N] и X 2 [N] , т.к. в силу (**) |
|||||||||
A[M, N] X |
1 |
[N] = A[M, N |
' ] X |
0 |
[N ' ] + ε A[M , N] λ[N] = b[M ] + ε 0[M ] = b[M ] |
||||
|
|
|
|
|
|
|
|
||
A[M, N] X |
2 |
[N] = A[M |
, N |
' ] X |
0 |
[N ' ] − ε A[M, N] λ[N] = b[M ] − ε 0[M ] = b[M ] |
|||
|
|
|
|
|
|
|
|||
Из определения векторов X1[N] и X 2 [N] следует, что |
|||||||||
|
|
1 |
|
|
|
|
1 |
X 2 [N], и X1[N], X 2[N] D !!! |
|
|
|
X[N] = |
|
X1 |
[N] + |
|
|
||
|
|
|
|
2 |
|||||
|
|
2 |
|
|
|
|
|
||
Последнее представление противоречит условию теоремы о том, что X 0 [N] - вершина множества D. Следовательно, неверным является исходное предположение о линейной зависимости столбцов матрицы A[M , N ' ] и, на самом деле, X 0 [N] является базисным решением ЗЛП. ■
7.5. Достижимость оптимального решения ЗЛП в угловой точке множества допустимых решений
Допустимое решение ЗЛП X *[N] является оптимальным решением ЗЛП (I), если допустимого решения ЗЛП X[N]
f (X * ) ≥ f (X )
Здесь мы докажем, что среди оптимальных решений ЗЛП всегда есть вершина множества D. Это утверждение позволяет искать оптимальное решение ЗЛП только среди базисных решений. Для доказательства этого утверждения, нам понадобится следующая лемма, которую мы сформулируем для случая выпуклого многогранника (ограниченного выпуклого многогранного множества).
Любая точка выпуклого многогранника может быть представлена в виде выпуклой линейной комбинации его вершин.

101
hЛинейная комбинация векторов {X1[N], , X s [N]}
s
∑λ[i] X i [N]
i=1
s
называется выпуклой, если 1) λ[i] ≥ 0 , (i 1: s) 2) ∑λ[i] =1h
i=1
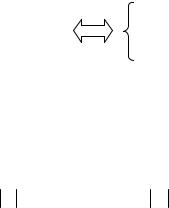
Проиллюстрируем доказательство леммы для плоского многоугольника. Пусть D - выпуклый многоугольник на плоскости с вершинами {X1 , X 2 , , X p } и пусть X D - произвольная
точка этого множества. Произведем триангуляцию D (его разбиение на непересекающиеся треугольники), соединив, например X1, со всеми остальными вершинами (см. Рис.).
X1


 X1
X1
Триангуляция
X 
X3
X
 X4
X4
Тогда точка Х попадет в один из элементов триангуляции (пусть это будет треугольник
|
|
|
|
|
~ |
|
X1 X3 X4, как на рисунке). Тогда точка Х лежит на отрезке [X |
1 , X ] и, следовательно, является |
|||||
выпуклой линейной комбинацией точек X1 |
|
~ |
|
|||
и |
X . |
|
||||
|
|
~ |
|
(0 ≤α ≤1) (*) |
|
|
~ |
|
X = αX1 + (1− α)X |
, |
|
||
, в свою очередь, лежит на отрезке [X3 , X 4 ] и может быть представлена в виде |
||||||
Но точка X |
||||||
|
|
~ |
|
, (0 ≤ β ≤1) |
|
|
|
~ |
X = βX 3 + (1− β)X 4 |
|
|||
Подставляя |
из последнего равенства в (*) находим |
|
||||
X |
|
|||||
X = αX1 |
+ (1− α)[β X3 + (1− β )X 4 ] = αX1 + (1− α)βX 3 |
+ (1− α)(1− β )X 4 = |
||||
= λ1 X1 + λ2 X 3 + λ3 X 4
Правая часть полученного соотношения есть линейная комбинация вершин. Убедимся в ее выпуклости.
1) λ1 = α ≥ 0, λ2 = (1−α)β ≥ 0, λ3 = (1− α)(1− β ) ≥ 0 2) λ1 + λ2 + λ3 = α + (1− α)β + (1− α)(1− β ) = α + (1− α)(β + 1− β ) = α + 1− α =1
Лемма доказана. Теперь переходим к доказательству утверждения (для случая выпуклого
многогранника).
102
Пусть X *[N]- оптимальное решение ЗЛП и {X1[N], , X p [N]} - вершины множества D.
Согласно лемме
X *[N] = λ[1] X1[N] + + λ[p] X p [N] Подставим X *[N] в целевую функцию ЗЛП
f (X * ) = λ[1] f (X1 ) + + λ[p] f (X p )
Выберем среди вершин ту, на которой достигается наибольшее (среди всех вершин) значение целевой функции. Пусть это будет вершина X k [N] : f (X k ) ≥ f (Xi ), i 1: p .
Тогда, заменяя в правой части последнего равенства |
f (X i ) на f (X k ) i 1: p , имеем |
||||||
|
|
|
|
|
|
|
p |
f (X * ) ≤ λ[1] f (X k ) + + λ[p] f (X k ) = f (Xk ) ∑λ[i] = f (X k ) |
|||||||
|
|
|
|
|
|
|
i=1 |
С другой стороны, f (X * ) ≥ f (X |
k |
) в силу оптимальности X *[N]. Таким образом |
|||||
|
|
|
|
|
|
|
|
окончательно получим f (X * ) = f (X |
k |
), т.е. вершина X |
k |
[N] тоже является оптимальным |
|||
|
|
|
|
|
|
||
решением ЗЛП. ■
7.6. Условия разрешимости ЗЛП. Конечность способа перебора вершин
Задача линейного программирования может быть неразрешима по одной из 2-х причин (см. раздел 1):
1)несовместность системы ограничений (множество D допустимых решений ЗЛП - пусто)
2)неограниченность целевой функции на множестве допустимых решений.
Если ни одна из этих причин не имеет места, то ЗЛП разрешима. Таким образом справедливо
утверждение
ЗЛП |
1) хотя бы одно допустимое решение |
разрешима |
2) целевая функция ЗЛП ограничена на множестве допустимых |
|
решений |
Обоснуем, в случае разрешимости ЗЛП, конечность способа перебора вершин множества D (или, что то же самое, конечность симплекс-метода, который является по сути направленным перебором последних).
1)Так как оптимальное решение ЗЛП достигается в одной из вершин множества D, то можно ограничиться рассмотрением только базисных решений ЗЛП.
2) Число базисных решений ЗЛП (I) конечно и ограничено сверху числом сочетаний из n = N элементов по m = M (см. П. 3.1.).
Следовательно, определив базисные решения, вычислив значения целевой функции на каждом из них и выбрав максимум, мы найдем оптимальное решение ЗЛП за конечное
число шагов.
7.7. Критерий оптимальности
Рассмотрим базисное решение ЗЛП с базисом N ' N
X0 [N] = (X 0 [N ' ], 0[N \ N ' ] )
ипроизвольное допустимое решение X[N], в котором выделим части относящиеся к
множествам индексов N ' и N \ N '
X[N] = (X[N ' ], X[ N \ N ' ] )
103
Так как X[N] - допустимое решение ЗЛП, то
A[M, N] X[N] = A[M, N ' ] X[N ' ] + A[M, N \ N ' ] X[N \ N ' ] = b[M ] Умножим последнее равенство слева на матрицу обратную к базисной
B[N ' , M ] A[M , N ' ] X[N ' ] + B[N ' , M ] A[M , N \ N ' ] X[N \ N ' ] = B[N ' , M ] b[M ] или
X[N ' ] = B[N ' , M ] b[M ] − Z[N ' , N \ N ' ] X[N \ N ' ]
Используя полученное выражение, вычислим значение целевой функции на решении X[N] f (X ) = C[N] X[N] = C[N ' ] X[N ' ] + C[N \ N ' ] X[N \ N ' ] =
= C[N ' ] B[N ' , M ] b[M ] − (C[N ' ] Z[N ' , N \ N ' ] − C[N \ N ' ]) X[N \ N ' ]
Введем обозначение |
|
|
|
ε[N] = C[N ' ] Z[N ' , N] − C[N] |
- вектор оценок текущего базисного решения X |
0 |
[N] |
|
|
|
hЛегко видеть, что (см. Определение Z[N ' , N] в п. 5.1.)
ε[N] = (ε[N ' ],ε[N \ N ' ]) = (C[N ' ] Z[N ' , N ' ] − C[N ' ],C[N ' ] Z[N ' , N \ N ' ] − C[N \ N ' ]) = = (0[N ' ],ε[N \ N ' ])
Т.о. оценки базисных переменных всегда равны нулю!h
С учетом введенных обозначений имеем
f (X ) = C[N ' ] B[N ' , M ] b[M ]−ε[N \ N ' ] X[N \ N ' ]
Подставляя в последнее равенство X 0 [N] вместо X[N] находим
f (X |
0 |
) = C[N ' ] B[N ' , M ] b[M ] |
(т.к. X[N \ N ' ] = 0[N \ N ' ] ) |
|
|
|
(это равенство можно получить также, определив X 0 [N ' ] из системы ограничений
A[M, N ' ] X |
0 |
[N ' ] = b[M ] , путем умножения ее на B[N ' , M ] . |
|
|
X0 [N ' ] = B[N ' , M ] b[M ]
ивычислив значение целевой функции).
Окончательно получим соотношение
f (X ) = f (X 0 ) − ε[N \ N ' ] X[N \ N ' ] Из данной формулы следует, что неравенство
f (X 0 ) ≥ f (X )
будет выполнено для любого допустимого X[N], если ε[N \ N ' ] X [N \ N ' ]≥ 0[N \ N ' ] . А т.к. X[N \ N ' ] ≥ 0[N \ N ' ], то достаточно выполнения неравенства
ε[N \ N ' ] ≥ 0[N \ N ' ]
Таким образом нами получено следующее условие оптимальности текущего базисного решения:
Если все компоненты вектора оценок ε[N] неотрицательны, т. е. ε[ j] ≥ 0 j N ,
то текущее базисное решение является оптимальным решением ЗЛП.
Пример. Рассмотрим ЗЛП
f = 2x1 + x2 + 5x3 − x4 → max
x1 + 2x2 |
+ x4 = 5 |
x2 + x3 |
+ 2x4 = 8 |
xi ≥ 0, |
i 1: 4 |
104
Пусть N ' ={1 , 3}, A[M, N ' ] = 1 |
0 , B[N ' , M ] = 1 |
0 |
, X [N] = (5,0,8,0) , |
||
0 |
1 |
|
0 |
1 |
0 |
|
|
|
|
|
|
1 |
2 |
0 |
1 |
|
|
Z[N ' , N] = B[N ' , M ] A[M, N ' ] = |
|
|
|
|
|
0 |
1 |
1 |
2 |
|
|
C[N] = (2,1,5,−1), C[N ' ] = (2 , 5) |
|
|
|
|
|
Вычисляем компоненты вектора оценок |
ε[ j] = C[N ' ] Z[N ' , j]− с[ j] |
||||
|
1 |
2 |
3 |
4 |
|
|
' |
2 |
1 |
5 |
-1 |
|
|
|
|
|
|
С[N ] |
|
|
С[N ] |
|
|
|
|
С[N '] |
|
|
|
|
|
|
||
2 |
1 |
2 |
0 |
1 |
|
|
|
|
|
|
Z [N ', N] |
|
|
5 |
|
|
|
|
2 |
|
0 |
1 |
1 |
2 |
|
|
|
|
|
|
|
|
|
5 |
|
0 |
8 |
0 |
13 |
ε[N '] |
|
Схема вычисления ε[2]:
c[2'] |
Вычитаем |
|
|
|
отсюда |
1 |
|
2 |
2·2+5·1=9-1=8 |
|
|
1 |
|
Z [N ', 2] |
|
Умножаем |
|
скалярно |
|
Получаем, что ε[N] = (0,8,0,13) ≥ (0,0,0,0) . Критерий оптимальности выполняется, а следовательно, текущее базисное решение является оптимальным и максимальное значение целевой функции равно
fMAX = 2 5 + 5 8 = 50
7.8.Улучшение текущего базисного решения ЗЛП. Критерий неограниченности
целевой функции на множестве решений
Пусть для текущего базисного решения X 0 [N] с базисом N ' нарушается условие оптимальности, т.е.
|
|
|
|
|
|
ε[ j |
0 |
] < |
0, j |
0 |
N \ N ' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Разобьем множество индексов N \ N ' |
на две непересекающиеся части N \ N ' = { j |
} N |
0 |
, |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
где N |
0 |
= (N \ N ' ) \ { j |
0 |
} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Предъявим теперь в качестве направления улучшения решения вектор |
|
|
|
|
|
||||||||||||||
|
|
Z[N] =ˆ |
(Z[N ' ], z[ j |
0 |
],Z[N |
0 |
]) = (B[N ' ,M ] A[M, j |
0 |
], −1, 0[N |
0 |
]) ( * ) |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
и выясним, при каких условиях вектор |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
Xθ [N] = X 0 [N]−θ Z[N], θ > 0-числовой параметр |
|
|
|
|
|
||||||||||||
будет допустимым решением ЗЛП |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Подставим Xθ [N]в систему ограничений ЗЛП |
|
|
|
|
|
|
|
||||||||||||
A[M , N ] X θ [ N ] = A[M , N ] |
X 0 [ N ] − θ A[M , N ] Z [ N ] = b[M ] (далее) |
|
|||||||||||||||||
2
5
105
т.к. A[M , N ] X 0 [ N ] = b[M ] , то для того, чтобы Xθ [N] удовлетворял системе ограничений, необходимо чтобы вектор Z[N] был решением однородной системы A[M , N ] Z [ N ] = 0[M ]
В соответствии с определением вектора Z[N] имеем
A[M , N ] B[ N ' , M ] A[M , j0 ] + A[M , j0 ] (−1) + A[M , j0 ] 0[ N 0 ] = = A[M, j0 ]− A[M, j0 ] = 0[M ]
Так как Xθ [N] удовлетворяет системе ограничений ЗЛП, то для допустимости необходима только его неотрицательность.
Xθ [N] = X0[N] −θ Z[N] ≥ 0[N]
Предположим сначала, что все компоненты вектора Z[N] неположительны, что с учетом (*) означает
|
|
|
|
|
|
Z[N ' ] = B[N ' , M ] A[M , j |
0 |
] ≤ 0[N ' ] |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В этом случае −θ Z[N] ≥ 0[N] |
θ > 0 и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
X0 [N] −θ Z[N] ≥ 0[N] θ > 0 |
|
|
|
|
|
|
|
|
|
|||||||||
Т.е. Xθ [N] - допустимое решение ЗЛП при любом положительном значении параметра θ . |
|
|||||||||||||||||||||||
Значение целевой функции на решении Xθ [N] равно |
|
|
|
|
|
|
|
|
|
|||||||||||||||
f (X |
θ |
) = C[N] X |
0 |
[N] −θ C[N] Z[N |
] = f (X |
0 |
) −θ (C[N ' ] Z[N |
' ] − с[ j |
0 |
]) = f (X |
0 |
) −θ ε[ j |
0 |
] |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Легко видеть, что при θ → +∞ , |
f (Xθ ) → +∞ , т.е. в случае неположительности вектора |
|
|
|||||||||||||||||||||
Z[N ' ] целевая функция неограничена на множестве решений ЗЛП. |
|
|
|
|
|
|||||||||||||||||||
Сформулируем условие неограниченности целевой функции на множестве допустимых |
|
|
||||||||||||||||||||||
решений |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Если при ε[ j |
0 |
] < 0 , все компоненты столбца |
|
j |
0 |
матрицы Z[N ' |
, N]: |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
Z[N ' , j |
0 |
] = B[N |
' ,M ] A[M, j |
0 |
] |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
меньше либо равны нулю, то целевая функция неограничена на множестве допустимых
решений ЗЛП.
Пример. Несколько видоизменим исходные данные в ЗЛП предыдущего примера
|
|
|
f |
= 2x1 + x2 |
+ 5x3 |
− x4 |
→ max |
|
|
|
|
|
|
||||
|
|
|
|
x1 − 2x2 |
|
|
|
+ x4 = 5 |
|
|
|
|
|
|
|
||
|
|
|
|
− x2 |
+ x3 |
|
+ 2x4 = 8 |
|
|
|
|
|
|
|
|||
|
|
|
|
xi |
≥ 0 , |
i 1: 4 |
|
|
|
|
|
|
|
|
|||
|
|
|
Z [N] = |
(-2, -1, -1, 0 ) |
|
|
|
|
|
5 |
− 2 |
5+ 2θ |
0 |
||||
1 |
2 |
3 |
4 |
x [N]= x |
|
|
|
|
|
|
|
|
|
θ |
|
|
|
2 |
1 |
5 |
-1 |
|
[N]−θ z[N]= 0 |
−θ |
−1 |
= |
|
≥ 0 |
|||||||
θ |
|
0 |
|
|
|
|
|
|
|
|
8+θ |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
8 |
|
−1 |
|
|
0 |
|
|
-2 |
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
0 |
|
0 |
|
-1 |
|
Z [N ', j 0] ≤ 0[N '] |
|
|
|
|
|
|
(5 + 2 θ )− 2 (θ )+1 0 = 5 |
|||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
-10 |
|
|
|
|
|
|
|
|
|
−θ + (8 +θ )+ 2 0 = 8 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
θ → ∞ |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
При |
|
|
|
|
|
|
|||
|
|
ε[j 0] |
|
|
|
|
|
|
|
|
2 (5 + 2 θ )+θ + 5 (8 +θ )→ ∞ |
||||||
|
|
|
|
|
|
|
f (x ) = |
||||||||||
|
|
|
|
|
|
|
|
|
θ |
|
|
|
|
|
|
|
|
Целевая функция неограничена на множестве решений ЗЛП
106
Значит для возможности улучшения текущего базисного решения необходимо наличие
хотя бы одной положительной компоненты вектора Z[N ' ] = B[N ' , M ] A[M , j |
0 |
] (или, что |
||||||
|
|
|
|
|
|
|
|
|
то же самое, столбца Z[N |
' , j |
0 |
] матрицы Z[N ' , N] ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обозначим множество индексов положительных компонент указанного вектора через N+ . |
||||||||
N |
+ |
= { j N ' : z[i] = B[i, M ] A[M , j |
0 |
] > 0} |
|
|
||
|
|
|
|
|
|
|
||
Среди компонент вектора Xθ [N] отрицательными могут стать только компоненты с индексами из N+
Xθ [N+ ] = X 0 [N+ ] −θ Z[N+ ]
(базисная компонента x0 [i] текущего решения уменьшается на величину −θ z[i]). Тогда, для сохранения допустимости решения Xθ [N], необходимо выбирать параметр θ из условия
θ ≤ |
x0 [i] |
, |
|
для всех |
i N |
|
|
|
|
||||||
|
|
+ |
|
|
|
||||||||||
|
z[i] |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
по правилу |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
x |
0 |
[i] |
|
|
x |
0 |
[i |
0 |
] |
|
||||
θ = min |
|
|
|
|
:i N+ |
= |
|
|
|
|
( + ) |
||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
z[i] |
z[i0 ] |
|
||||||||||||
При этом будет обеспечена и неизменность числа базисных компонент решения Xθ [N] |
|||||||||||||||
(в новом решении компонента xθ [i0 ] обратится в нуль, т..е. выйдет из числа базисных, а |
|||||||||||||||
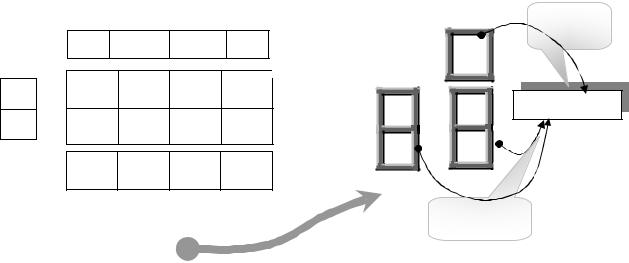
компонента xθ [ j0 ] =θ > 0 станет базисной). Такой переход к решению Xθ соответствует
замене в базисе A[M , N ' |
] столбца A[M ,i |
0 |
] |
на столбец A[M , j |
0 |
] (т.е. замене базисного |
|||||
|
|
|
|
|
|
|
|
|
|
||
множества индексов N ' |
на N |
' |
= N |
' \ {i |
} { j |
}). |
|
|
|||
|
|
1 |
|
0 |
|
|
|
0 |
|
|
|
i 0
A[M,N']
j 0
A[M,N\N']
Так выглядит схема замены столбцов в базисной матрице 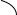
Пример. Рассмотрим ту же ЗЛП, изменив в ней коэффициенты при неизвестной x4 f = 2x1 + x2 + 5x3 − x4 → max
x1 + 2x2 |
+ x4 = 5 |
x2 + x3 |
− 2x4 = 8 |
xi ≥ 0 , |
i 1: 4 |
107
|
|
|
1 |
2 |
3 |
4 |
|
|
|
|
|
|
|
|
|
С[N '] X[N '] N ' |
2 |
1 |
5 |
-1 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
x[1] |
|
= |
5 |
= 5 |
|
|||
|
|
|
|
|
|
|
N+={1} |
θ = min |
|
|
1 |
|
|||
1 |
2 |
5 |
1 |
2 |
0 |
1 |
|
|
z[1,4] |
|
|
|
|||
3 |
5 |
8 |
0 1 1 -2 |
|
|
5 |
1 |
|
0 |
||||||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
8 |
0 |
-7 |
x |
[N] = x |
[N] −θ z[N] = 0 |
− 5 |
0 |
|
= 0 |
|
|
|
|
|
θ |
0 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
8 |
− 2 |
|
18 |
|||
Переменная х1 |
|
|
|
|
|
|
0 |
|
−1 |
|
5 |
|
|||
выйдет из числа |
|
|
ε[4]<0 Переменная х4 |
|
|
|
|
|
|
|
|
||||
|
базисных |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
войдет в базис |
|
|
|
|
|
|
|
|
|
hЗначение целевой функции на новом базисном решении f (Xθ ) = f (X 0 ) −θ ε[ j0 ]
увеличивается на f = −θ ε[ j0 ]. Указанное произведение называется величиной скачка целевой функции ( f ) при переходе к новому решению. Так в вышеприведенном примере
f (Xθ ) = f (X 0 ) −θ ε[4] = 50 − 5 (−7) = 85 f = −θ ε[4] = 35
Величина f может быть использована как определяющая для вектора наилучшего направления при переходе к новому решению (см. замечание к алгоритму симплекс-метода в п.3.3)h
Таким образом, окончательно можно резюмировать, что если ε[ j0 ] < 0 и критерий неограниченности не выполняется ( N+ ≠ 0/ , т.е. среди компонент вектора Z[N ' ] есть хотя бы одна положительная), то выбрав значение θ > 0 по правилу (+), получим новое
решение ЗЛП Xθ [N], причем |
|
|
|
|
|
xθ [ j0 ] =θ |
|
|
|||
x |
[ j] = x |
0 |
[ j] −θ z[ j] , j N |
' \{i |
} |
θ |
|
|
0 |
|
|
xθ [ j] = 0 |
|
для всех остальных |
j N |
||
которое “лучше” решения X0[N] |
|
в смысле значения целевой функции |
|||
|
f (Xθ ) = f (X0 ) −θ ε[ j] > f (X0 ) |
|
|||
7.9. Базисная матрица нового решения ЗЛП. Левый мультипликатор. Формулы исключения Гаусса-Жордана
Так как матрица, заменившая в новом решении базисную матрицу A[M , N ' ] отличается от нее только одним столбцом, то для базисности новой матрицы A[M , N1' ] достаточно доказать следующую лемму: