Задачи ЛП и методы их решения
.pdf
|
|
|
|
|
|
|
|
129 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
a −1 |
|
|
|
|
|
||
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
a |
2 |
|
0 |
|
|
|
|
|
a |
−1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||
A[M, N ']= |
|
|
|
|
|
|
|
|
B[N ',M ]= |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
m |
|
|
|
|
|
|
a |
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
||
Далее для заполнения начальной симплекс-таблицы вычисляют:
|
|
|
|
|
|
|
c[i1 ] |
|
|
|
c[im |
] |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v[M ]=C[N '] B[N ',M ]= |
,..., |
|
|
|
||||||||||||||
|
am |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
a1 |
|
|
|
|
|
|
|
||||
0 [ |
] |
[ |
] |
[ |
M |
] |
= |
b[1] |
,..., |
b[m] |
||||||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
||||||||||||||
x |
N ' |
= B |
N ',M |
b |
|
|
|
|
|
|
|
|
|
|||||
f (x0 )=C[N '] x[N '] |
|
|
|
a1 |
|
|
|
|
am |
|
|
|
||||||
= ∑c[ik ] b[k] |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k=1 |
|
|
|
|
a |
k |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
В любом случае, для построения начального базисного решения, можно воспользоваться искусственным базисом, решая вспомогательную задачу
g =0[N ] x[N ]+1[N1 ] x[N1 ]→ min
|
[ |
] |
[ |
] |
[ |
M, N |
1 ] |
[ |
N |
1 ] |
[ |
M |
] |
|
|||||||||||||
A |
M, N |
x |
N |
+E |
|
x |
|
=b |
|
||||
|
|
x[N ]≥0[N ], x[N1 ]≥0[N1 ] |
|
|
|||||||||
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь x[N1 ] - искусственные переменные ( N1 = M =m). Если выбрать их в качестве базисных ( N ' = N1 ), то начальная базисная матрица и обратная к ней будут единичными
x0 [N ']=b[M ], v[M ]=1[M ], g(x0 )=1[M ] b[M ]
Когда все искусственные переменные станут небазисными, текущий базис будет соответствовать допустимому базисному решению исходной задачи и для построения начальной симплекс-таблицы следует заменить вектор коэффициентов целевой функции на C[N ] и пересчитать v[M ] и f (x0 ) .
Если хотя бы одна искусственная переменная останется базисной с положительным значением в оптимальном решении вспомогательной задачи это будет соответствовать неразрешимости исходной ЗЛП из-за несовместности системы ограничений.
Таким образом, начальная симплекс-таблица и вспомогательная таблица для подсчета оценок будут иметь вид:
|
f (x0 ) |
v[M ] |
|
C[N ] |
N ' |
x0 [N '] |
B[N ',M ] |
v[M ] |
A[M, N ] |
|
|
|
|
ε[N ] |
Первый шаг. Вычисление оценок и проверка текущего решения на оптимальность
Вычисляем во вспомогательной таблице оценки небазисных векторов
ε[j]= v[M ] A[M, j]−C[ j]
ипроверяем условие оптимальности
ε[j]≤0
|
|
|
130 |
|
Если все оценки неположительны, то текущее базисное решение является |
||||
оптимальным и алгоритм завершает работу. |
|
|||
Если же оценка |
ε[j0 ]>0 , то она записывается первым элементом дополнительного |
|||
столбца симплекс-таблицы, а вектор |
|
|||
|
|
|
z[N ', j0 ]= B[N ',M ] A[M, j0 ] |
|
в оставшуюся часть дополнительного столбца. |
|
|||
|
f (x0 ) |
v[M ] |
ε[j0 ] |
C[j0 ] |
N ' |
x[N '] |
B[N ',M ] |
z[N ', j0 ] |
A[M, j0 ] |
|
|
|||
|
|
|
|
ε[j0 ] |
|
|
|
B[N ',M ] A[M, j0 ] |
|
Таким образом, при нарушении условия оптимальности, текущее базисное решение может |
||||
быть улучшено путем введения в базис столбца A[M, |
j0 ]. |
|||
Второй шаг. Определение вектора, выводимого из базиса и проверка критерия |
||||
неограниченности целевой функции на множестве допустимых решений |
||||
Определяем величину θ из условия
|
|
|
|
|
|
|
|
|
|
x[i] |
|
|
|
|
x |
[i0 ] |
|
|
|
|
|
|
|
|||
θ =min |
|
|
|
z[i, j0 ]>0 |
= |
|
|
|
|
] |
z[i0 , j0 |
] |
|||||
z[i, j0 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Индекс i0 N ' определяет вектор A[M,i0 ], который будет выведен из базиса и заменен
вектором A[M, j0 ].
Если θ невозможно определить из приведенного условия (все компоненты вектора z[N ', j0 ] неположительны), то целевая функция ЗЛП неограниченна на множестве
допустимых решений.
Третий шаг. Переход к новому базисному решению N '' = N '\ {i0} {j0} (индекс i0 заменяется на j0 )
Основная часть симплекс-таблицы преобразуется по формулам метода полного исключения Гаусса-Жордана с ведущим элементом z[i0, j0 ].
|
ε[j0 ] |
|
|
i0 |
z[i0 |
, j0 |
] |
|
|||
j0 |
|
|
|

|
|
|
|
|
|
|
|
|
|
|
|
131 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
T |
|
T |
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
ij |
|
|
ij0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ti j |
|
Ti j |
|
|
i0 |
||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
0 |
0 0 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
T* |
= |
Ti0 , j |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
i , j |
|
Ti |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, j |
|
|
|
|
|
|
|
|
|
|
|
||||
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T* |
=T − |
Ti0 , j Tij0 |
|
|
|
|
|
|
|
||||||||
i, j |
|
ij |
|
|
|
Ti |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|||||
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
||||
x[j0 ]=θ
При этом x[i0 ]=0
f (x)= f (x0 )− f = f (x0 )−ε[ j0 ] θ
После преобразования основной части симплекс таблицы в ней будет содержаться информация о новом (улучшенном) базисном решении
|
f (x) |
v[M ] |
|
|
|
N '' |
x[N ''] |
B[N '',M ] |
|
|
|
На этом одна полная итерация модифицированного симплекс-метода заканчивается, и совершается переход к шагу 1.
Пример Рассмотрим ЗЛП на минимум f = x1 +2x2 −x3 → min
|
|
|
|
x +x |
|
+x =6 |
|
|
||||
|
|
|
|
1 2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x1 +x2 |
|
+3x3 =10 |
|
||||||
{ } |
|
|
x1 ≥0, x2 ≥0, x3 ≥0 |
) |
||||||||
|
|
|
{ |
} |
[ |
N |
] |
= |
( |
|||
M = 1,2 , N = 1,2,3 |
|
, C |
|
1,2, |
−1 |
|||||||
A[M, N ]= |
1 1 1 |
b[M ]= |
6 |
|
|
|||||||
|
2 |
1 |
, |
|
|
|
|
|||||
|
|
3 |
|
|
|
|
10 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
Т. к. единичный и диагональный начальные базисы отсутствуют, воспользуемся искусственным базисом и рассмотрим вспомогательную задачу
g = |
|
+x4 + x5 → min |
|||
|
x |
+ x |
+ x + x |
|
=6 |
|
1 |
2 |
3 |
4 |
|
|
|
||||
|
|
|
|
|
|
2x1 |
+ x2 |
+3x3 |
|
+ x5 =10 |
|
xi ≥0, i 1: 5
Начальный базис, отвечающий искусственным переменным будет единичным
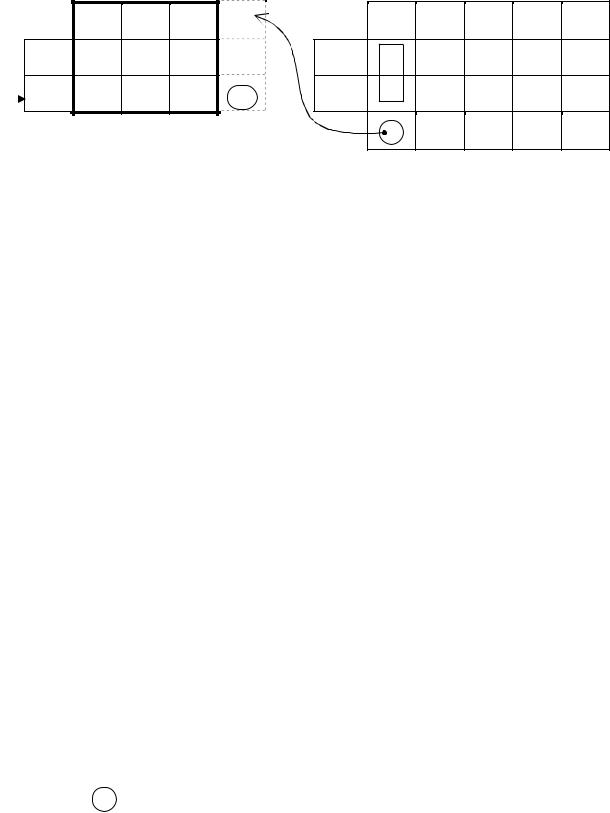
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
132 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N ' = |
{ } |
|
[ |
] |
= |
1 |
0 |
|
[ |
N ', |
M |
] |
|
1 |
0 |
|
|
[ |
N |
] |
( |
) |
|
|
|
|
|
|
|||||||
|
0 |
1 |
|
|
|
0 |
1 |
|
|
|
|
|
|
|
|
||||||||||||||||||||
4,5 |
|
, A M |
, N ' |
|
|
, B |
|
= |
|
|
|
, C |
' |
= 1,1 |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[ |
M |
] |
[ |
|
] |
[ |
N ',M |
] |
= |
( ) |
[ |
] |
|
|
[ |
N ',M |
] |
[ |
M |
] |
|
6 |
( ) |
[ |
] |
[ |
] |
=16 |
|||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||
v |
|
=C |
N ' |
B |
|
1,1 |
|
. x |
N ' |
= B |
|
|
b |
|
= |
; f |
x |
=C |
N ' |
x |
N ' |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Начальная симплекс-таблица запишется в виде
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
N |
N ' |
16 |
1 |
1 |
3 |
v[M ] |
0 |
0 |
0 |
1 |
1 |
C[N ] |
|
|||||||||||
4 |
6 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
|
|
|
||||||||||
5 |
10 |
0 |
1 |
2 |
1 |
2 |
1 |
3 |
0 |
1 |
|
|
|
||||||||||
|
|
|
|
|
|
3 |
2 |
4 |
0 |
0 |
ε[N ] |
Вычисляем оценки, используя вспомогательную таблицу |
|
|
|
|
|
||||||
ε[1]=v[M ] A[M,1]−C[1]=(1,1) 1 −0 =3
2
ε[2]=v[M ] A[M,2]−C[2]=(1,1) 1 −0 =2
1
ε[3]=v[M ] A[M,3]−C[3]=(1,1) 1 −0 =4
3
|
[ |
|
] |
|
[ |
|
|
|
] |
|
|
|
[ |
|
|
|
|
] |
|
[ |
|
|
] |
|
( |
) |
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||||||
|
4 |
=v |
M |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
−1=0 |
|
|
|
|
|
|
||||||||||||||||||||||||
|
ε |
|
|
|
|
A M,4 |
|
|
−C |
|
|
|
= |
1,1 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|||
|
[ |
|
] |
|
[ |
|
|
|
] |
|
|
[ |
|
|
|
] |
|
|
[ |
|
|
] |
|
|
( |
) |
|
0 |
|
|
|
|
|
|
|
|
|
||||||||||
|
5 |
=v |
M |
|
|
|
|
|
|
|
5 |
= |
|
|
|
−1=0 |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
ε |
|
|
|
|
A M,5 |
|
|
−C |
|
|
1,1 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
[ |
] [ |
|
] |
|
|
|
|
[ |
|
] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
2 |
и ε |
3 |
положительны) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Решение не оптимально (ε 1 ,ε |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
Выберем для ввода в базис вектор A[M,1] |
|
( j0 =1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Вычислим вектор |
z[N ',1]= B[N ',M ] A[M,1] |
= |
2 |
(совпадает |
с |
A[M,1], |
т. к. |
B[N ',M ] |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[ ] |
в дополнительный столбец симплекс- |
|||||||||||||||||||||
единичная) и запишем его вместе с оценкой ε |
|
1 |
|||||||||||||||||||||||||||||||||||||||||||||
таблицы. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
10 |
|
10 |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
[ |
|
|
|
|
z[i, j0 ]> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(i0 |
=5), |
|
|||||||||||||||||
Найдем величину |
θ = min |
|
|
|
|
|
|
|
|
|
|
0 |
= min |
|
|
|
|
, |
|
|
|
= |
|
=5 |
которая |
||||||||||||||||||||||
|
|
|
i, j |
|
|
|
1 |
2 |
2 |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
z |
|
] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
[ |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[ |
|
|
] |
). |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
определяет вектор, выводимый из базиса (в данном случае это A M,5 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
Заменяем в столбце N ' индекс 5 на индекс 1 и преобразуем основную часть симплекстаблицы (выделена) по формулам полного исключения Гаусса-Жордана с ведущим элементом 2

|
|
|
|
|
133 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
N '' |
1 |
1 |
-1/2 |
1/2 |
|
|
v[M ] |
0 |
0 |
0 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
1 |
1 |
-1/2 |
1/2 |
|
1 |
1 |
1 |
1 |
1 |
0 |
|
1 |
5 |
0 |
1/2 |
1/2 |
|
|
-1/2 |
2 |
1 |
3 |
0 |
1 |
|
|
|
|
|
|
|
|
0 |
1/2 |
-1/2 |
0 |
-3/2 |
Получаем новое базисное решение, для которого подсчитываем оценки. Условие
оптимальности не выполняется для вектора |
[ |
|
|
] |
. Вводим его в базис вместо вектора |
|||||||||||||||||
A M,2 |
|
|||||||||||||||||||||
[ |
] |
, т. к. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
A M,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
1 |
−1/2 |
|
1 |
|
1/2 |
|
|
θ |
|
|||
z[N ',2]= B[N ',M ] A[M,2]= |
|
|
|
|
|
|
= |
|
|
, и |
достигается на индексе 4 |
|||||||||||
|
0 |
1/2 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1/2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
1 |
|
5 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
θ = min |
|
, |
|
= |
|
|
=2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
1/2 |
1/2 |
1/2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Преобразуем симплекс-таблицу и переходим к новому базисному решению, в котором все искусственные переменные из базиса выведены. Значит, это решение является допустимым базисным решением исходной задачи. Переходим к исходной задаче, заменяя вектор C[N ], пересчитывая в симплекс-таблице вектор v[M ] и значение целевой функции
f (x), и новые оценки во вспомогательной таблице без искусственных переменных.
|
|
|
|
|
|
|
|
N ''' |
|
0 |
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
4 |
|
|
|
|
-1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[ |
N |
] |
( |
) [ |
] |
= |
( |
) [ |
M |
] |
= |
( |
) |
|
2 |
|
−1 |
|
3 |
f |
( |
x |
) |
=8 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
C |
|
= 1,2, |
−1 , C |
N ' |
|
|
2,1 , v |
|
|
2,1 |
|
|
|
|
= |
, |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
1 |
|
−1 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
3 |
|
|
|
|
|
|
|
8 |
|
3 |
|
|
|
-1 |
|
1 |
|
|
|
|
|
|
|
v[M ] |
|
1 |
|
|
|
2 |
|
-1 |
C[N ] |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
2 |
2 |
|
2 |
|
|
|
-1 |
|
-1 |
|
|
|
|
|
|
|
3 |
|
1 |
|
|
|
1 |
|
1 |
|
||||||
|
|
|
|
1 |
4 |
|
-1 |
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
-1 |
|
2 |
|
|
|
1 |
|
3 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
1 |
ε[N ] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
134 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вектор A[M,3] |
«просится» в базис ( j0 =3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
x[1] |
|
|
4 |
|
|
|
|
|
|
|||
|
|
z |
[ |
N ',3 |
] |
= |
−1 |
1 |
= −1 |
θ = |
|
= |
|
= 2 |
( |
i |
=1 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
z 1,3 |
2 |
|
|
0 |
) |
|
|||||||
|
|
|
|
|
|
|
|
−1 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[ |
] |
|
|
|
|
|
|
|
|
||||||
[ |
|
|
] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
вместо вектора A M,1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
6 |
|
7/2 |
|
|
-3/2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
-1 |
||||
|
2 |
|
4 |
|
3/2 |
|
|
0 |
|
|
|
|
|
|
|
|
|
7/2 |
|
1 |
|
|
1 |
1 |
|||||||
|
3 |
|
2 |
|
-1/2 |
|
|
1/2 |
|
|
|
|
|
|
|
|
|
|
-3/2 |
|
2 |
|
|
1 |
3 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-1/2 |
|
0 |
0 |
||
Критерий оптимальности (все оценки неположительны) Получено оптимальное базисное решение
x* =(0,4,2), f (x*)= fmin = 2 4−1 2 =6
Рассмотрим теперь параллельное описание обоих алгоритмов симплекс-метода – прямого и модифицированного, сравним их по объему требуемой памяти и числу операций.
Прямой алгоритм с-м |
Модифицированный алгоритм с-м |
|||||
|
|
C[N ] |
|
f (x) |
v[M ] |
ε[j0 ] |
|
|
|
|
|||
N ' C[N '] |
x[N '] |
z[N ', N ] |
m |
|
|
|
|
|
|
m |
x[N '] |
B[N ',M ] |
z[N ', j0 ] |
|
|
|
N ' |
|
||
|
f (x) |
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
n |
|
|
|
|
1.Хранится и перерабатывается |
|
z[N ', j0 ]= B[N ',M ] A[M, j0 ] |
||||
следующая информация: |
|
|
|
|
|
|
N '- множество индексов текущего базиса |
|
|
|
|
|
|
|
C[N '] - коэффициенты целевой функции, |
m |
v |
[ |
M |
] |
A M, N |
] |
|
|
|
[ |
||||
соответствующие базисным переменным |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε[j0 ] |
x[N ']= B[N ',M ] b[M ] - базисная часть |
|
|
|
|
|
|
|
|
|
|
|
|
|
(j0 ) |
|
текущего решения |
|
|
|
|
|
|
n


|
|
|
|
|
|
136 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
Требуемая память |
|
|
|||||||||||
|
|
= n - число переменных, |
|
M |
|
= |
|
N ' |
|
= m - число ограничений) |
|||||||||
|
( |
N |
|
|
|
|
|||||||||||||
( |
)( ) |
= |
|
|
|
|
|
|
Вспомогательная таблица: |
||||||||||
|
|
|
|
|
|
||||||||||||||
2m+n + |
m +1 n +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
=2m+n +mn +m+n+1= |
|
|
|
|
|
|
m+(m+2)n |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
=3m+2n +mn +1 чисел |
|
|
|
|
|
|
Основная таблица: |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
m+(m+1)(m+2) |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
Всего: m+mn +2n +m+m2 +3m+2 = |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
=3m+2n +mn +1+ |
( |
m+1 2 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
Число операций
(Выбор θ и просмотр оценок не учитывается. На преобразование одного элемента по методу исключения требуется 4 арифметические операции)
4m(n+1)+(n+1)= (4m+1)(n+1)- |
|
|
|
4m(m+1) |
- |
преобразование симплекс- |
||||||||||||||||||||
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
таблицы |
|
|
|
|
|
|
|
|
|
|
|
||||
арифметических операций |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
(m+1)(n+1) - операций присваивания |
|
|
(2m−1)n+n - вычисление оценок ε[N ] |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
) |
|
|
|
|
|
|
|
|
|
[ |
0 ] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2m−1 m |
- вычисление вектора z |
N ', j |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Всего |
|
4m(m+1)+(2m−1)(m+n)+n |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
арифметических операций |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
(m+1)(m+1)+m+n |
|
- |
|
операций |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
присваивания |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
После несложных преобразований, находим |
|
|
|
|
|
|||||||||||||||||
(4m+1)(n+1) |
|
|
|
|
|
|
|
|
(4m+1)(n+1)−[(n +1)(2m +1)−m(6m +1)] |
|||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
(m+1)(n+1) |
|
|
|
|
|
|
|
|
( |
m+1 n+1 − mn−m |
m+2 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
)( |
) |
|
|
( |
|
|
) |
|
|||||
|
|
|
|
|
|
|||||||||||||||||||||
|
|
Выражения в квадратных скобках положительны при |
|
|
||||||||||||||||||||||
|
|
|
|
m |
( |
6m +1 |
|
|
|
|
2m |
|
|
|
|
|
1 |
|
|
|
|
|
||||
|
|
n > |
|
|
) |
−1 |
=3m−1− |
=3m−2+ |
|
|
|
|
|
|||||||||||||
|
|
|
|
) |
|
|
|
|
|
|
|
|
||||||||||||||
( |
|
|
|
|
|
|
|
|
2m+1 |
|
|
|
|
2m+1 |
|
|
||||||||||
|
|
|
|
|
2m+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
и
137
n >m+2
При m ≥2 имеем n ≥3m−2
Если учитывать только операции деления, то получим
(с учетом определения θ)
(m+n+1) - делений |
(m+m+1) - делений |
||
|
|
|
|
Все эти данные приведены для одной итерации алгоритмов. Опыт решения ЗЛП показал относительную независимость числа итераций от числа переменных (n) и существенную зависимость его от числа ограничений (m). В среднем, оно (число итераций) колеблется от m до 3m.
Таким образом, к «почти квадратным» ЗЛП (примерно одинаковое число ограничений и переменных) лучше применять прямой С-М, а к ЗЛП «вытянутым в ширину» (неизвестных значительно больше, чем ограничений) – модифицированный С-М.
Решим посредством прямого и модифицированного алгоритмов С-М следующую задачу:
|
|
|
f = x1 + x2 + x3 + x4 + x5 |
+ x6 + x7 + x8 |
+ x9 → min |
|
|
|
|||||||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x +2x |
+ x + x |
|
+ x |
|
|
=100 |
|
|
|||||
|
|
|
|
|
|
1 |
2 |
3 |
|
4 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
+2x3 + x4 |
|
+4x6 +3x7 +2x8 + x9 =100 |
(*) |
|
|
|||||
|
|
|
|
|
x1 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xi ≥0, (i 1: 9). |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если |
это возможно, |
удобнее |
|
всего |
выбирать на |
начальном |
шаге N ' так, |
что |
|||||||||
A[M, N ']= E[M, N '] |
- единичная матрица. Тогда B[N ',M ]= E[N ',M ] - тоже единичная |
||||||||||||||||
матрица |
и |
[ |
N ', N |
] |
совпадает с |
|
|
[ |
] |
|
|
[ |
M |
] |
|||
z |
|
A M, N |
, а вектор двойственных переменных v |
|
|||||||||||||
совпадает с C[N '] |
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||
N ' ={5,9}, |
A[M, N ']= E[M, N '], |
B[N ',M ]= E[N ', M ] |
|
|
|
|
|||||||||||
x[N ']=(100,100), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
Прямой с-м |
|
|
|
|
|
Модифицированный с-м |
|
|
|||||
Нулевой шаг (Заполнение начальной симплекс-таблицы)
[ |
|
|
|
] |
|
[ |
|
|
] |
|
[ |
] |
[ |
] |
|
[ |
|
] |
[ |
] |
[ |
|
] |
[ |
] |
( ) |
z |
N ', N |
|
= B |
N ',M |
A M,N |
= A |
M ', N |
= |
v |
M |
|
=C |
N ' |
B |
N ',M |
|
=C |
N ' |
= 1,1 |
|||||||
= |
2 |
2 |
|
1 |
1 |
1 0 0 0 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
1 |
0 |
|
2 |
1 |
0 |
4 |
3 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|