
Задачи ЛП и методы их решения
.pdf
149
 13
13

 9
9

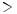
 5
5

 1
1

 0
0
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
13 |
12 |
11 |
10 |
|
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
Если обозначить через u[i] - путь максимальной доходности из вершины i в вершину 0 и положить u[0]=0 , то можно записать соотношение
u[i]= max{v[k]+u i−l[k] k Ni } (*)
( Ni - множество дуг, выходящих из вершины i )
Это соотношение называется функциональным уравнением Р.Беллмана или функциональным уравнением динамического программирования.
Чуть позже мы вернемся к уравнению (*) и дадим его интерпретацию в терминах потенциалов для сетевой транспортной задачи, а сейчас займемся его решением.
В данной задаче имеется простой способ решения уравнения Беллмана: достаточно вычислять v[i] последовательно от v[1] до v[L], запоминая управление (номер заготовки)
на котором достигался максимум. Будем формировать список, каждый элемент которого состоит из размера сырья, получаемого из этого сырья дохода, и заготовки, которую следует отрезать от сырья этого размера. Список должен быть упорядочен по возрастанию размеров сырья и строго упорядочен по доходам. Будем говорить, что запись с размером сырья λ1 и доходом γ1 доминирует ( α ) запись λ2 , γ2 , если λ1 ≤λ2 и γ1 ≥γ2 . Собственно списков будет два – рабочий (текущий) список и архивный список. На каждом шаге к самой первой из имеющихся в рабочем списке записей будет прибавляться каждая из заготовок: размер сырья будет при этом равен сумме размера в исходной записи и длины прибавляемой детали, доход будет равен сумме имеющегося дохода и цены прибавляемой заготовки, в качестве отрезаемой заготовки будет указана эта прибавляемая заготовка. Полученный набор новых записей вливается в рабочий список с соблюдением условий упорядочения: по длине и по доходу. Записи, которые доминируются другими, исключаются из списка. Записи, в которых размер сырья превосходит L , в список также не включается. Использованная таким образом первая запись рабочего списка, передается в архивный список, а процесс повторяется до исчерпания рабочего списка.
Проследим работу алгоритма на нескольких первых шагах того же примера, что и в методе ветвей и границ.
На шаге 2 запись (20, 20, 20) исключается из рабочего списка, так как доминируется кандидатом (18, 20, 9). На шаге 3 из рабочего списка удаляется запись (29, 30, 20), доминируемая кандидатом (27, 30, 9), а кандидат (38, 40, 20) не включается в рабочий список, так как доминируется записью рабочего списка (37, 40, 37). На четвертом шаге, по этой же причине, кандидат (58, 63, 37) не включается в рабочий список (доминируется записью рабочего списка (58, 65, 40)). Продолжаем перерабатывать рабочий список.
шаг |
Архивный список |
Рабочий список |
Кандидаты в рабочий |
|
список |
||||
|
|
|

150
|
|
|
9, 10, 9 |
|
|
|
|
20, 20, 20 |
|
1 |
− |
(0, 0, 0) |
21, 23, 21 |
|
|
|
|
37, 40, 37 |
|
|
|
|
40, 45, 40 |
|
|
(0, 0, 0) |
(9, 10, 9) |
18, 20, 9 |
|
|
|
× (20, 20, 20) |
29, 30, 20 |
|
|
|
|
|
|
|
|
(21, 23, 21) |
|
|
2 |
|
30, 33, 21 |
||
|
(37, 40, 37) |
|
|
|
|
|
46, 50, 37 |
||
|
|
|
||
|
|
(40, 45, 40) |
|
|
|
|
|
|
|
|
|
|
49, 55, 40 |
|
|
(0, 0, 0) |
(18, 20, 9) |
27,30,9 |
|
|
(9, 10, 9) |
(21, 23, 21) |
|
|
|
|
× |
||
|
|
|
38,40,20 |
|
|
|
× (29, 30, 20) |
|
|
|
|
{ |
|
|
3 |
|
(30, 33, 21) |
39,43,21 |
|
|
|
|
||
|
(37, 40, 37) |
55,60,37 |
|
|
|
|
|
||
|
|
(40, 45, 40) |
|
|
|
|
|
|
|
|
|
(46, 50, 37) |
58,65,40 |
|
|
|
|
|
|
|
|
(49, 55, 40) |
|
|
|
(0, 0, 0) |
(21, 23, 21) |
(30, 33, 9) |
|
|
(9, 10, 9) |
(27, 30, 9) |
|
|
|
|
|
(41,43,20) |
|
|
(18, 20, 9) |
× (30, 33, 21) |
|
|
|
|
|
||
|
|
(37, 40, 37) |
42,46,21 |
|
|
|
( |
) |
|
4 |
|
(39, 43, 21) |
(58,63,37) |
× |
|
(40, 45, 40) |
|||
|
|
(61,68,40) |
|
|
|
|
(46, 50, 37) |
|
|
|
|
|
|
|
|
|
(49, 55, 40) |
|
|
|
|
(55, 60, 37) |
|
|
|
|
(58, 65, 40) |
|
|
После исчерпания рабочего списка остается следующий архивный список:
Размер |
доход |
Заготов. |
Размер |
доход |
Заготов. |
Размер |
доход |
Заготов. |
сырья |
|
|
сырья |
|
|
сырья |
|
|
9 |
10 |
9 |
57 |
63 |
21 |
80 |
90 |
40 |
18 |
20 |
9 |
58 |
65 |
40 |
82 |
91 |
40 |
21 |
23 |
21 |
60 |
66 |
21 |
84 |
93 |
21 |
27 |
30 |
9 |
61 |
68 |
40 |
85 |
95 |
40 |
30 |
33 |
21 |
63 |
70 |
9 |
87 |
96 |
21 |
36 |
40 |
9 |
66 |
73 |
21 |
88 |
98 |
40 |
39 |
43 |
21 |
67 |
75 |
40 |
89 |
100 |
40 |
40 |
45 |
40 |
69 |
76 |
21 |
91 |
101 |
40 |
42 |
46 |
21 |
70 |
78 |
40 |
93 |
103 |
21 |
45 |
50 |
9 |
72 |
80 |
9 |
94 |
105 |
40 |
48 |
53 |
21 |
75 |
83 |
21 |
96 |
106 |
21 |
49 |
55 |
40 |
76 |
85 |
40 |
97 |
108 |
40 |
51 |
56 |
21 |
78 |
86 |
21 |
98 |
110 |
40 |
54 |
60 |
9 |
79 |
88 |
40 |
100 |
111 |
40 |
Искомый раскрой получается обратным просмотром архивных записей:
|
|
151 |
|
|
|
|
|
Запись архивного списка |
|
Способ раскроя |
|
|
|
|
9, 20, 21, 37, 40 |
(100, 111, 40) |
|
(0, 0, 0, 0, +1) |
|
(60, 66, |
21) |
|
(0, 0, +1, 0, 1) |
(39, 43, |
21) |
|
(0, 0, 1+1, 0, 1) |
(18, 20, 9) |
|
(+1, 0, 2, 0, 1) |
|
(9, 10, |
9) |
|
(1+1, 0, 2, 0, 1) |
Искомый способ раскроя (2, 0, 2, 0, 1) с доходом 111.
В процедуре, приведенной ниже, используется более удобный в вычислительном отношении вариант уравнения Беллмана
|
|
|
|
|
|
max{u[i,k −1],v[k]+u i−l[k],k }, i ≥l[k] |
|||||
u[i,k]= |
[ |
] |
[ |
k |
] |
|
|||||
u |
i,k −1 , i <l |
|
|||
|
|
|
|
|
|
Его решение реализуется способом, использующим вместо матрицы u вектор, в котором последовательно получаются все строки этой матрицы:
Процедура r -задачи методом динамического программирования
{v[0:l0]– вектор в котором получаются последовательно все строки матрицы.
Dec[0:l0]– целочисленный массив решений
(номер отрезаемой детали), принимаемых в состояниях процесса }
for I:=0 step 1 until l0 do begin v[i]:=0; dec[i]:=0 end;
{начальные установки}
for k:=1 step 1 until n do {цикл по номерам деталей} begin ck:=c[k]; lk:=l[k]; x[k]:=0;
{текущие доход и длина}
for I:=lk step 1 until l0 do
{цикл по длине сырья от текущей до l0} if v[I-lk]+ck>v[I] then
begin v[i]:=v[I-lk]+ck; dec[i]:=k end
{Если встретился рекорд, то принимается решение отрезать деталь с номером k}
end k; d:=l0;
{Начало восстановления раскроя. Индекс устанавливается равным l0}
for I:=dec[d] while I>0
{при I=0 достигнем нулевой части вектора dec} begin x[i]:=x[i]+1; d:=d-l[i] end
{Элемент массива x (раскрой) с индексом, равным номеру очередной отрезаемой детали увеличивается на единицу. После окончания цикла в нем получается искомый Наилучший способ раскроя}.
И хотя изложенный алгоритм генерации способа раскроя является одним из наиболее эффективных, его затруднительно применить при наличии дополнительных ограничений на используемые способы раскроя (ограничение на число заготовок в раскрое,

152
выделенные типы заготовок: «только в середине», «только с края» и т. д.). В этом случае, по-видимому, предпочтительнее алгоритм метода ветвей и границ.
Итак, возвращаясь к постановке задачи линейного раскроя, констатируем, что решение проблемы генерации способов раскроя (столбцов матрицы системы ограничений) позволяет избавиться от хранения матрицы всех возможных способов раскроя.
Базисную матрицу, отвечающую начальному базисному решению, можно выбрать диагональной
A[M, N ']=diag( L/l[i] , i M )
Тогда
B[N ',M ]= diag(L/l[i] −1 , |
i M ) |
|
|
|
|
|||||||||||
x[N ']= B[N ', M ] b[M ] |
|
|
|
|
|
|
|
|
||||||||
f |
( |
[ |
N ' |
]) |
[ |
] |
[ |
] |
=1 |
[ |
] |
[ |
] |
[ |
M |
] |
|
x |
|
=1 |
N ' |
x |
N ' |
|
N ' |
B |
N ',M |
b |
|
||||
v[M ]=1[N '] B[N ', M ]=(L/l[i]−1 , i M ).
Общая схема модифицированного симплекс-метода выглядит следующим образом:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
v[M ] |
|
|
|
|
e −1 |
|
|
r − задача |
|||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e = v[M ] r[M ] → max |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
r[M ] l[M ] ≤ L |
||
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
A[M, N ' ] |
|
x[N ' ] |
|
B[N',M] |
|
|
|
|
z[N' ] |
|
|
|
r[M ] ≥ 0[M ] |
||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
r[M ] − целочисленный |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
z[N'] = B[N',M] r[M] |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Пусть теперь x* [N ] - оптимальное решение задачи линейного раскроя. f * =1[N ] x* [N ] -
минимальное значение целевой функции. В [22] показано, что существует целочисленное решение задачи раскроя со значением целевой функции
|
|
f |
* |
|
+1 (ε |
- достаточно мало). |
|
||||||
f = |
|
−ε |
||||
|
|
|
|
|
|
|
Подсчитаем остаток вектора требований
b[M ]=b[M ]− A[M, N ] x* [N ]
и разобьем его на
k = f −1[N ] x* [N ]
раскроев. Для этого можно использовать часть процедуры bestpartition[9] в режиме r-
задачи при m =k и z = L .Объединяя полученный набор из k |
раскроев r1[M ],...,rk [M ] с |
|||||
единичными интенсивностями с базисным набором |
|
|
|
|
||
|
* |
с интенсивностями |
|
|
* |
, |
A M, N |
|
x N |
|
|||
|
|
|
|
|
|
|
имеем оптимальное целочисленное решение исходной задачи линейного раскроя.

153
Рассмотрим пример с исходными данными, приведенными выше ( L =35,l =(9,5,3)) и
вектором требований b =(101,101,102).
Выпишем из вышеприведенной матрицы всех возможных способов раскроя, только технологичные раскрои (отход меньше чем длина самой короткой заготовки) и перенумеруем их (выделены безотходные раскрои)
|
1 |
2 |
|
|
3 |
4 |
|
|
5 |
6 |
|
7 |
8 |
9 |
|
10 |
|
11 |
12 |
13 |
14 |
15 |
16 |
|
|
17 |
|
|
18 |
19 |
|
20 |
|
|
Номер раскроя |
|
|||||||||||||||||||||||||||||||||||
3 |
3 |
|
|
2 |
2 |
|
|
2 |
2 |
|
1 |
1 |
1 |
|
1 |
|
1 |
1 |
0 |
0 |
0 |
0 |
|
|
0 |
|
|
0 |
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
1 |
0 |
|
|
3 |
2 |
|
|
1 |
0 |
|
5 |
4 |
3 |
|
2 |
|
1 |
0 |
7 |
6 |
5 |
4 |
|
|
3 |
|
|
2 |
|
1 |
|
|
0 |
|
Способ раскроя |
||||||||||||||||||||||||||||||||||||
|
1 |
2 |
|
|
0 |
2 |
|
|
4 |
5 |
|
0 |
2 |
3 |
|
5 |
|
7 |
8 |
0 |
1 |
3 |
5 |
|
|
6 |
|
|
8 |
|
10 |
|
11 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
0 |
2 |
|
|
2 |
1 |
|
|
0 |
2 |
|
1 |
0 |
2 |
|
|
1 |
|
0 |
2 |
|
0 |
2 |
1 |
0 |
|
|
2 |
|
|
1 |
|
0 |
|
|
2 |
|
|
|
|
Отход |
|||||||||||||||||||||||||||||||
Выберем в качестве начальной базисной матрицы диагональную |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(*) |
|
13 |
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
0 |
|
|
|
|
0 |
|
|
|
|
* 1/3 |
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A[M, N '] |
|
|
0 |
|
7 |
|
0 |
|
|
B[N ', M ]= |
13 |
|
|
0 |
|
|
1/7 |
|
0 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
11 |
|
|
|
|
80 |
|
|
0 |
|
|
|
0 |
1/11 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Построим начальную симплекс-таблицу МСМ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
13252 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
54 |
|
|
|
|
|
|
r -задача: ε |
|
=ε 1 = |
54 |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
231 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
7 |
|
|
|
|
|
11 |
|
|
231 |
|
|
|
|
|
|
|
|
|
|
|
max |
|
[ |
] |
|
231 |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
101 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
1 |
|
||||||||||||
(*) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
z[N ',1]= B[N ',M ] |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 = |
1/7 |
|
|||||||||||||||||||||||
|
|
|
|
101 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
13 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1/11 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
20 |
|
|
102 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Переходим к новому решению |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
11434 |
|
|
|
59 |
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
12 |
|
|
|
|
|
|
|
r -задача: ε |
|
=ε 19 |
= |
12 |
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
231 |
|
|
|
|
|
231 |
|
|
|
|
7 |
|
|
|
|
11 |
|
|
|
231 |
|
|
|
|
|
|
|
|
|
max |
|
|
[ |
] |
|
|
|
231 |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
101 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
0 |
|
||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z[N '',19]= B[N '',M ] |
|
1 |
= |
1/7 |
|
|||||||||||||||||||
|
|
|
|
|
202 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
13 |
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
10/11 |
|||||||||||||||||||||||||||
|
|
|
21 |
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
20 |
|
|
|
|
205 |
|
|
|
|
|
- |
1 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
1 |
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Получаем новое базисное решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение оптимально, т. к. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
344 |
|
|
|
|
9 |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
7 |
|
|
|
|
35 |
|
|
|
|
|
|
35 |
|
|
|
|
|
35 |
|
|
v |
[ |
M |
] |
= |
( |
9,5,3 |
и |
v |
[ |
M |
] |
A M, j |
=1 |
|
|
|
для |
любого |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
35 |
|
) |
|
|
|
|
|
|
[ |
|
] |
|
|
|
|
|
|
|
|
|
|
|||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
безотходного |
раскроя |
|
[ |
|
|
j |
] |
и |
меньше |
единицы для |
|||||||||||||||||||||||||||||||||||
|
|
|
3 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
605 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A M, |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
13 |
|
|
|
605 |
|
|
|
|
- |
3 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
- |
1 |
|
каждого раскроя с ненулевым отходом. А значит, |
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε[j]≤0 j N |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
70 |
|
|
|
|
70 |
|
|
|
|
7 |
|
|
|
|
|
|
70 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
19 |
|
|
|
205 |
|
|
|
|
- |
1 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
30 |
|
|
|
|
30 |
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
154
Выпишем оптимальное решение
2 |
3 |
|
9 |
|
0 |
|
5 |
0 |
|
|
101 |
||||||
|
|
+8 |
|
|
|
+6 |
|
|
|
= |
|
|
|||||
33 |
|
|
|
7 |
|
1 |
|||||||||||
|
|
1 |
|
|
|
|
|
|
|
101 |
|||||||
3 |
|
|
14 |
|
|
6 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
10 |
|
|
102 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Перейдем к нахождению оптимального целочисленного решения. Округлим значение целевой функции вверх до ближайшего целого
Найдем остаток вектора требований |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
101 |
3 |
|
0 |
|
|
0 |
|
|
|
|
101−99 |
|
|
2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
b |
= 101 −33 |
1 −8 |
7 −6 |
1 |
|
= 101−33−56−6 |
= |
6 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
102 |
1 |
|
0 |
|
10 |
|
|
102−33−60 |
|
|
9 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Подсчитаем число разбиений |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
k = |
f |
−(1 33+1 8+1 6)=50−47 =3 |
|
|
|
||||||||||||||||||
Разбиваем остаток вектора требований на 3 раскроя |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
0 |
0 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
6 |
= |
|
1 + |
|
4 + 1 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
4 |
|
|
|
5 |
0 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(0) (0) |
(30) |
|
|
|
|
|
|
||||||
Получаем оптимальное целочисленное решение |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
3 |
0 |
|
0 |
|
|
2 |
0 |
0 |
101 |
|
|
|||||||||||
33 |
1 +8 |
7 +6 |
|
1 |
+1 |
1 +1 |
4 |
+1 1 |
= 101 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
1 |
|
0 |
|
10 |
|
|
|
4 |
|
5 |
|
0 |
102 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
со значением целевой функции |
f |
=50. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||

155
7.14. Особенности форматного раскроя бумажного полотна
Предприятие, выпускающее бумагу и картон различных марок, получает заявки от покупателей на количество тонн бумаги (картона) определенной марки рулонами различных размеров (форматов1). Примерная заявка имеет вид:
Требуется бумага (марка) в следующих форматах:
№ п/п |
Формат (мм) |
Количество (т) |
|
|
|
1 |
1260 |
50 |
2 |
1000 |
100 |
3 |
840 |
150 |
|
|
|
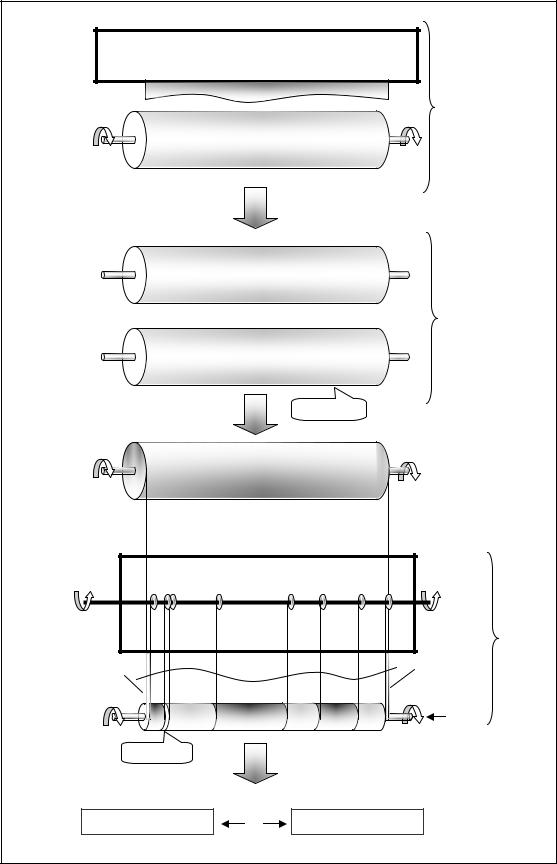
Бумага с бумагоделательной машины (БДМ) поступает в виде бумажного полотна в тамбурах2 длиной l0 (6300 мм), которые в дальнейшем разрезаются на продольно-
резательном станке (ПРС) в виде рулонов определенного диаметра и формата. Нарезание рулонов осуществляется по раскладкам (способам раскроя), в которых указывается по сути расположение ножей ПРС по ширине тамбура в соответствии с нарезаемыми форматами по данной раскладке. Однократное нарезание рулонов по раскладке называется съемом. По каждой раскладке указывается необходимое количество съемов (интенсивность или кратность использования способа раскроя). Суммарное количество рулонов каждого формата, нарезанное по всем раскладкам с учетом их кратностей, должно быть равно требуемому количеству рулонов, которое задается вектором требований. При этом суммарный попутный отход по всем раскладкам должен быть минимальным.
Главной особенностью данной задачи форматного раскроя является то, что в заявке необходимое количество бумаги по форматам задается в тоннах, а при нарезании форматов на ПРС подсчитывается необходимое число рулонов. Эта особенность не являлась бы важной в том случае, если бы существовала однозначная зависимость между рулоном определенного формата и его весом. Однако, по причинам технологического характера, вес рулона определенного формата колеблется в некоторых пределах, и при нарезании бумаги рулонами возможен “уход” тоннажа формата в меньшую или большую сторону.
Помимо этого, в задаче имеется ряд дополнительных ограничений:
1)ширина способа раскроя не должна превышать полезную ширину тамбура
2)с края тамбура нужно резать обязательную кромку, которая находится в диапазоне
[min Edge, max Edge]
3)минимальный вырезаемый рулон должен быть не меньше минимального расстояния между ножами либо минимального заданного формата, не входящего в заявку («попутчика») в зависимости от того какая, из двух величин будет больше
4)рулоны меньше определенного формата должны вырезаться парами и располагаться в способе раскроя рядом
1 Здесь под форматом понимается только ширина рулона.
2 Вал с намотанным на него бумажным полотном, вышедшим из БДМ. Ширина вала колеблется обычно от 2,5 до 9 метров.
|
|
|
156 |
|
|
Б |
Д |
М |
|
|
|
тамбур |
|
|
|
|
накат |
|
|
|
|
|
Зона брака |
|
|
П Р С |
|
||
Кромка |
|
|
|
Кромка |
|
|
|
|
|
|
|
рулон |
|
съём |
|
попутчик |
|
|
|
склад |
упаковка |
|
На производство |
|
5)некоторые форматы имеют дополнительные требования: а) нельзя ставить на край б) нужно обязательно с краю
6)нужно учитывать количество ножей на ПРС (количество заготовок в раскрое)

157
7)возможно несколько зон постоянного брака
8)если бракованная зона меньше минимального рулона, то ее нужно рассматривать как плавающую зону брака, содержащую в себе реальный бракованный промежуток
9)в подавляющем большинстве случаем вектор требований размыт частично или полностью в определенном диапазоне b1[M ] ≤ b[M ] ≤ b2[M ]
10)иногда есть рулоны, которые не требуются в заказах, но их можно выпускать неограниченно. При этом количество таких выпущенных рулонов нежно свести к минимуму.
11)Имеется допустимая погрешность намотки рулонов. ПРС в состоянии намотать рулон с точностью до миллиметра, при этом допустима погрешность до 5мм.
12)Имеется погрешность выполнения заказа.
13)Имеется приоритет выполнения заказов.
14)Общее требование: отход не должен превышать максимальной кромки.
15)В процессе нарезания возможны корректировки требований на форматы и число рулонов по следующим причинам:
-Технологический брак при изготовлении бумаги и ее разрезании.
-Ввод дополнительного формата в текущую заявку (административное решение). Очевидно, что наличие выявленного технологического брака в рулонах приводит к исключению уже нарезанных рулонов из заявки “форматы-рулоны” и требует пересмотра плана раскроя “раскладки-съемы”. Введение дополнительного формата в заявку также вынуждает находить раскладки и их интенсивности использования (количество съемов) заново. Уточнение веса нарезанных рулонов может также привести к необходимости корректировки заявки “форматы-рулоны”, а, значит, и к нахождению нового плана раскроя.
Некоторые из приведенных ограничений (1-2,6,14) относятся к формированию способа раскроя (раскладки) и должны учитываться при решении r – задачи. Другие ограничения либо вносят изменения в постановку задачи раскроя, либо требуют замены самой постановки. Как правило, во всех задачах раскроя бумажного полотна требуется находить целочисленное решение.
Перейдем к рассмотрению основных вариантов задач линейного форматного раскроя бумажного полотна. Начнем с целочисленной задачи линейного раскроя.
Задача целочисленного линейного раскроя
Постановка задачи.
Пусть имеется одномерное сырье (тамбур) длины L (ширина тамбура), из которого необходимо вырезать заготовки (рулоны) различных типов из множества M (| M |= m – число элементов в множестве M , в нашей задаче m – число различных форматов в заявке). Длины заготовок задаются вектором l[M ] (форматы рулонов в заявке). Вектор b[M ] задает необходимое для производства количество заготовок (вектор требований на вырезаемые рулоны). Требуется, удовлетворив вектор требований (ВТ) на заготовки, израсходовать минимальное количество штук сырья.
Пусть теперь N – множество номеров всех возможных способов раскроя тамбура (множество номеров всех возможных раскладок, включая и нетехнологичные, либо по количеству вырезаемых заготовок, либо с большим отходом). N = n – число всех
возможных способов раскроя. Составим из способов раскроя целочисленную неотрицательную матрицу A[M, N], где A[M, j] – способ раскроя с номером j. A[i, j] – количество заготовок i-го типа, вырезаемых j-м способом раскроя (число рулонов i-го формата в j – ой раскладке). Неотрицательный вектор способа раскроя A[M, j], очевидно, удовлетворяет ограничению
|
158 |
l[M ] A[M , j] ≤ L |
(*) |
так как суммарная длина вырезаемых в способе заготовок не должна превышать длины сырья.
Введем целочисленный неотрицательный вектор неизвестных x[N] – интенсивности (количество раз) использования способов раскроя. x[ j] – интенсивность j-го способа раскроя.
Ясно, что однократное использование способа раскроя приводит к израсходованию одной штуки сырья длиной L . Тогда функция f (x) = 1[N] x[N] выражает суммарное количество израсходованных штук сырья на вырезание всех требуемых заготовок. У данной функции мы должны найти минимум при условии вырезания всех заготовок
A[M, N] x[N] = b[M ]
Таким образом, приходим к следующей задаче f (x) = 1[N] x[N] → min
A[M, N] x[N] = b[M ] x[N] ≥ 0[N]
x[N] – целочисленный,
в которой столбцы матрицы A[M, N] удовлетворяют ограничению (*).
Если к ограничениям этой задачи добавить еще два (соответствующих максимуму концевого отхода и максимальному количеству вырезаемых в способе раскроя заготовок)
l[M ] A[M , j] ≥ L − p , |
j N, p − максимальный концевой отход |
A[M , j] 1[M ] ≤ k −1, |
k – максимальное число ножей на ПРС |
то получим задачу целочисленного программирования, реализующую нахождение оптимальных раскладок и их интенсивностей.
Метод решения задачи
Для этой задачи можно применить комбинированный алгоритм решения целочисленной задачи линейного раскроя.
Суть его заключается в следующем. Изначально решается задача линейного раскроя без условия целочисленности посредством модифицированного симплекс-метода (МСМ) с тем изменением, что матрица раскроев A[M, N] не хранится, а необходимый для ввода в
базис столбец (наилучший раскрой r[M ] = A[M, j0 ]) генерируется из условия r[M ] v[M ] → max , где v[M ]-вектор двойственных переменных (r-задача)[3]. При этом, очевидно, если величина ε[ j0 ] = r[M ] v[M ]−1≤ 0 , то текущее решение оптимально, т.к. оценки остальных столбцов будут еще меньше. В противном случае найденный столбец
A[M , j0 ] вводится в базис. |
|
|
||||
После того, как решение линейной задачи раскроя x*[N] найдено, |
его |
целевую |
||||
функцию (суммарное число съемов) округляют вверх до ближайшего целого |
|
|
||||
K = [ f *]+1 (1[N] x*[N] = f * ) , |
|
(3.1) |
||||
а само решение разделяют на целую и дробную части. |
|
|
||||
x*[N] = [x*[N]]+{x*[N]} = |
|
+α[N] |
|
(3.2) |
||
x |
|
|||||
Затем выделяют остаток вектора требований |
|
|
||||
|
|
[M ] = A[M, N] α[N] – целочисленный и разбивают его на |
|
|
||
b |
k |
раскроев, |
||||
используя какой-либо комбинаторный метод, где |
|
|
||||
k = 1[N] α[N]+ (1−{ f *}). |
|
(3.3) |
||||
