
- •Конспект лекций
- •2. Основные операции над матрицами
- •Тема 2 Определители и их свойства.
- •1. Определители и их свойства
- •2. Ранг матрицы
- •3. Обратная матрица
- •Тема 3. Элементы линейной алгебры в экономике
- •1. Линейная модель международной торговли
- •2. Модель Леонтьева многоотраслевой экономики
- •Тема 4 Системы линейных алгебраических уравнений
- •1. Системы линейных алгебраических уравнений. Теорема Кронекера Капелли
- •2. Применение определителей к исследованию и решению систем линейных уравнений. Формулы Крамера
- •1. Решение систем линейных алгебраических уравнений методом обратной матрицы
- •2. Решение систем линейных алгебраических уравнений методом Гаусса
- •Тема 5 Элементы векторной алгебры
- •1. Векторы. Координаты вектора
- •2. Линейные операции над векторами
- •3. Скалярное и векторное произведение векторов
- •Тема 6. Элементы высшей алгебры
- •Тема 7 Элементы аналитической геометрии
- •1. Уравнение линии на плоскости
- •2. Прямая линия на плоскости
- •3. Полярные координаты
- •1. Канонические уравнения эллипса, гиперболы, параболы
- •2. Преобразования декартовой системы координат на плоскости
Тема 6. Элементы высшей алгебры
Лекция 1.6.1. «Элементы высшей алгебры»
Учебные вопросы:
Комплексные числа
Действия над комплексными числами
Комплексные числа
Число
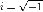 называется
мнимой единицей. Можно рассматривать
мнимую единицу как формальный объект,
который имеет следующее свойство:
называется
мнимой единицей. Можно рассматривать
мнимую единицу как формальный объект,
который имеет следующее свойство: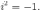
Комплексные
числа
 - это пара
- это пара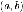 действительных чисел с заданными
определенным образом операциями
умножения и сложения. Комплексное число
действительных чисел с заданными
определенным образом операциями
умножения и сложения. Комплексное число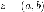 записывают как
записывают как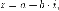
Число
 называетсядействительной
частью
числа
называетсядействительной
частью
числа
 ,
а число
,
а число —мнимой
частью
числа
—мнимой
частью
числа
 .
Их обозначают
.
Их обозначают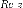 и
и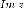 соответственно:
соответственно:
Таким образом, комплексное число задается двумя действительными числами. Если интерпретировать эти числа как декартовы координаты, то получим естественное соответствие комплексных чисел и точек на плоскости.
Если в случае действительных чисел мы имели числовую прямую, то в случае комплексных чисел получаем числовую плоскость, которая называется комплексной плоскостью.
Пусть
 Тогда число
Тогда число называетсякомплексно-сопряженным
или просто сопряженным
к числу
называетсякомплексно-сопряженным
или просто сопряженным
к числу
 .
.
Модулем
комплексного числа
 называется число
называется число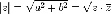 - длина отрезка
- длина отрезка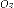 на
комплексной плоскости.
на
комплексной плоскости.
Модуль комплексного числа есть неотрицательное действительное число. Модуль равен нулю тогда и только тогда, когда само число равно нулю.
Модуль произведения комплексных чисел равен произведению их модулей.
Аргумент
комплексного
числа - это
угол
 между
осьюOX
и вектором OP,
изображающим это комплексное число.
Отсюда, tan
между
осьюOX
и вектором OP,
изображающим это комплексное число.
Отсюда, tan
 =b
/ a
.
=b
/ a
.
Тригонометрическая
форма комплексного числа.
Абсциссу a
и ординату b
комплексного
числа a +
bi можно
выразить через его модуль r
и аргумент
 :
:
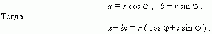
Действия над комплексными числами
Операции
сложения и умножения комплексных чисел
осуществляются так, как если бы мнимая
единица
 была
переменной (а комплексные числа —
многочленами от этой переменной), при
этом
была
переменной (а комплексные числа —
многочленами от этой переменной), при
этом .
.
Сложение. Суммой комплексных чисел a+ bi и c+ di называется комплексное число ( a+ c ) + ( b+ d ) i. Таким образом, при сложении комплексных чисел отдельно складываются их абсциссы и ординаты.
Это определение соответствует правилам действий с обычными многочленами.
Вычитание. Разностью двух комплексных чисел a+ bi (уменьшаемое) и c+ di (вычитаемое) называется комплексное число ( a – c ) + ( b – d ) i.
Таким образом, при вычитании двух комплексных чисел отдельно вычитаются их абсциссы и ординаты.
Умножение. Произведением комплексных чисел a+ bi и c+ di называется комплексное число:
( ac – bd ) + ( ad + bc ) i . Это определение вытекает из двух требований:
1) числа a+ bi и c+ di должны перемножаться, как алгебраические двучлены,
2) число i обладает основным свойством: i 2 = –1.
Деление. Разделить комплексное число a+bi (делимое) на другое c+ di (делитель) - значит найти третье число e+fi (чатное), которое будучи умноженным на делитель c+ di, даёт в результате делимое a+ bi.
Если делитель не равен нулю, деление всегда возможно.
Примеры.
1.
Записать комплексное число
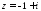 в тригонометрической и показательной
формах.
в тригонометрической и показательной
формах.
Решение.
Полагаем
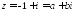 .
Вычислим модуль комплексного числа
.
Вычислим модуль комплексного числа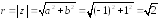 .
.
На
основе соотношения
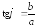 вычислим
вычислим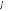 – аргумент комплексного числа
– аргумент комплексного числа .
Теперь можно записать комплексное число
в тригонометрической форме
.
Теперь можно записать комплексное число
в тригонометрической форме
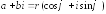 ,
,
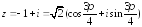 .
.
Используя формулу Эйлера, переходим к показательной форме комплексного числа:
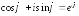 ,
,
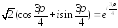
2.
Выполнить деление комплексных чисел
 .
.
Решение.
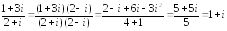
3.
Вычислить
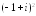 .
.
Решение.
Полагаем
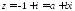 .
Запишем данное комплексное число в
тригонометрической форме (см. пример
1).
.
Запишем данное комплексное число в
тригонометрической форме (см. пример
1).
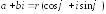 ,
,
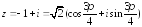
Далее применим формулу Муавра
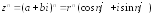
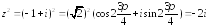
4.
Вычислить
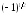 .
.
Решение.
Полагаем
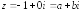 .
Запишем данное комплексное число в
тригонометрической форме (см. пример
1).
.
Запишем данное комплексное число в
тригонометрической форме (см. пример
1).
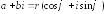 ,
,
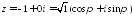
Далее применим формулу
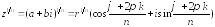 ,
,

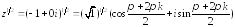 ,
,

При
 имеем
имеем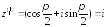
При
 имеем
имеем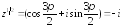
Таким
образом,
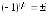 .
.
