
- •Конспект лекций
- •2. Основные операции над матрицами
- •Тема 2 Определители и их свойства.
- •1. Определители и их свойства
- •2. Ранг матрицы
- •3. Обратная матрица
- •Тема 3. Элементы линейной алгебры в экономике
- •1. Линейная модель международной торговли
- •2. Модель Леонтьева многоотраслевой экономики
- •Тема 4 Системы линейных алгебраических уравнений
- •1. Системы линейных алгебраических уравнений. Теорема Кронекера Капелли
- •2. Применение определителей к исследованию и решению систем линейных уравнений. Формулы Крамера
- •1. Решение систем линейных алгебраических уравнений методом обратной матрицы
- •2. Решение систем линейных алгебраических уравнений методом Гаусса
- •Тема 5 Элементы векторной алгебры
- •1. Векторы. Координаты вектора
- •2. Линейные операции над векторами
- •3. Скалярное и векторное произведение векторов
- •Тема 6. Элементы высшей алгебры
- •Тема 7 Элементы аналитической геометрии
- •1. Уравнение линии на плоскости
- •2. Прямая линия на плоскости
- •3. Полярные координаты
- •1. Канонические уравнения эллипса, гиперболы, параболы
- •2. Преобразования декартовой системы координат на плоскости
Тема 4 Системы линейных алгебраических уравнений
Лекция 1.4.1 «Системы линейных алгебраических уравнений: общая теория»
Учебные вопросы:
Системы линейных алгебраических уравнений.
Теорема Кронекера Капелли
Применение определителей к исследованию и решению систем линейных уравнений, формулы Крамера.
1. Системы линейных алгебраических уравнений. Теорема Кронекера Капелли
Рассмотрим
систему m
линейных алгебраических уравнений с n
неизвестными
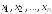 :
:

Здесь
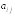
коэффициенты
системы (
коэффициенты
системы (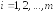
номер уравнения (строки),
номер уравнения (строки),
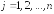
номер неизвестной, при которой данный
коэффициент стоит),
номер неизвестной, при которой данный
коэффициент стоит),
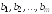
свободные
члены системы.
Если все свободные члены равны нулю
(
свободные
члены системы.
Если все свободные члены равны нулю
( ,
, ),
то система называется однородной, в
противном случае
неоднородной.
Если не оговорено особо, будут
рассматриваться неоднородные системы.
),
то система называется однородной, в
противном случае
неоднородной.
Если не оговорено особо, будут
рассматриваться неоднородные системы.
Система
может не иметь решений (уравнения
несовместны),
иметь единственное решение (единственный
набор значений неизвестных
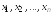 ),
иметь бесчисленное множество решений.
),
иметь бесчисленное множество решений.
Составим
из коэффициентов
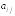 при неизвестных матрицу
при неизвестных матрицу

и
назовем ее матрицей
системы.
Матрицу
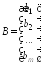 называютматрицей-столбцом
из свободных членов,
а матрицу
называютматрицей-столбцом
из свободных членов,
а матрицу
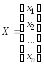 –
матрицей-столбцом из неизвестных.
Матрицу
–
матрицей-столбцом из неизвестных.
Матрицу
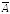 ,
полученную из матрицы
,
полученную из матрицы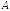 добавлением столбца свободных членов,
называют
добавлением столбца свободных членов,
называют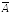 расширенной
матрицей системы:
расширенной
матрицей системы:
 .
.
Теорема
Кронекера
Капелли: система
m
линейных алгебраических уравнений с n
неизвестными имеет решение в том и
только в том случае, если матрица системы
и расширенная матрица системы имеют
один и тот же ранг
 .
В противном случае уравнения несовместны.
.
В противном случае уравнения несовместны.
Единственное
решение существует, если
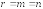 .
.
Если
обе матрицы имеют ранг
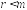 ,
то уравнения системы линейно
зависимы и
некоторые
,
то уравнения системы линейно
зависимы и
некоторые
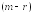 можно выразить в виде линейных комбинаций
остальных
можно выразить в виде линейных комбинаций
остальных уравнений (независимых), и им удовлетворяют
решения этих
уравнений (независимых), и им удовлетворяют
решения этих уравнений.Линейно
независимые
уравнения определяют некоторые
уравнений.Линейно
независимые
уравнения определяют некоторые
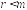 неизвестных как линейные функции
остальных
неизвестных как линейные функции
остальных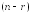 неизвестных, остающихся произвольными.
неизвестных, остающихся произвольными.
Если
обе матрицы имеют ранг
 ,
то уравнения системы линейно независимы.
,
то уравнения системы линейно независимы.
Пример. Исследовать систему линейных уравнений
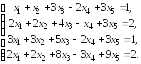
◄ Составим расширенную матрицу системы и с помощью указанных около нее элементарных преобразований найдем одновременно ранги обеих матриц:

Прибавив к четвертой строке последней матрицы третью строку, получаем
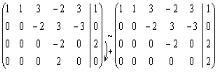 .
.
Ранг матрицы системы равен трем, так как ее преобразованная матрица имеет три ненулевых строки, а ранг расширенной матрицы равен четырем. Тогда согласно теореме Кронекера-Капелли система не имеет решений. ►
2. Применение определителей к исследованию и решению систем линейных уравнений. Формулы Крамера
Рассмотрим
систему n
линейных алгебраических уравнений с n
неизвестными
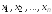 :
:
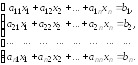
Составим
из коэффициентов
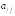 при неизвестных определитель
при неизвестных определитель
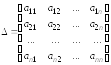
и
назовем его определителем
системы.
Если
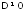 ,
то система имеетединственное
решение
,
то система имеетединственное
решение
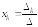 (
(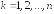 )
(правило
Крамера),
)
(правило
Крамера),
где

определитель, получающийся из
определитель, получающийся из
 при замене элементовk-го
столбца соответствующими свободными
членами
при замене элементовk-го
столбца соответствующими свободными
членами
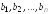 .
.
Если
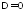 ,
а среди
,
а среди есть не равные нулю, тосистема
не имеет
решения.
есть не равные нулю, тосистема
не имеет
решения.
Пример. Решить методом Крамера систему уравнений
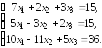
◄ Вычисляем
определитель системы:
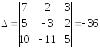 .
Система совместна и имеет единственное
решение, так как
.
Система совместна и имеет единственное
решение, так как .
.
Вычисляем вспомогательные определители:
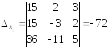 ,
,
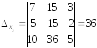 ,
,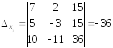 .
.
По
формулам Крамера получаем:
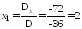 ,
,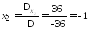 ,
,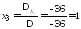 .
►
.
►
Лекция 1.4.2 «Решение систем линейных алгебраических уравнений методами обратной матрицы и Гаусса»
Учебные вопросы:
Решение систем линейных алгебраических уравнений методом обратной матрицы
Решение систем линейных алгебраических уравнений методом Гаусса
