2.2. Условия геометрической неизменяемости стержневых систем

Стержневыми системами называются системы, состоящие из отдельных, обычно прямолинейных, стержней, соединенных между собой в узлах с помощью сварки, заклепок, болтов или других скреплений;

Типичным примером стержневых систем являются фермы. В большинстве случаев соединения стержней фермы в узлах являются жесткими — не шарнирными. Точный расчет фермы с такими узлами весьма сложен, так как обычно она является много раз статически неопределимой системой. Если жесткие узлы фермы условно заменить шарнирными, то расчет ее значительно упрощается и при известных условиях может быть выполнен с помощью одних лишь уравнений статики. Опытные данные и теоретические исследования

Рис. 2.7

показывают, что такая замена допустима, так как при сосредоточенных нагрузках, приложенных в узлах, усилия,

возникающие в шарнирной ферме, мало отличаются от усилий в ферме с жесткими узлами (в случае, когда стержни имеют достаточно большую длину). Поэтому в дальнейшем будем пользоваться условной расчетной схемой фермы со стержнями, шарнирно соединенными в узлах.

Если заменить жесткие узлы системы, состоящей из трех стержней (изображенной на Рис. 2. 7, а), шарнирами, то система останется геометрически неизменяемой (Рис. 2. 7, б), т. е. такой, изменение формы которой возможно лишь в связи с деформациями ее элементов.

Если же заменить жесткие узлы шарнирами в системе, состоящей из четырех стержней (изображенной на Рис. 2. 8, а), то получится система геометрически изменяемая (Рис. 2. 8, б), т. е. такая, форма которой может меняться без деформации ее элементов.

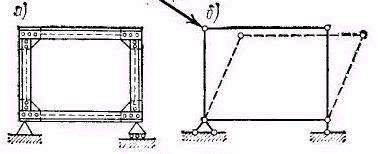
Рис. 2. 8

Наипростейшей геометрически неизменяемой, сочлененной из отдельных элементов, шарнирной системой (фермой) является система, состоящая из трех стержней, соединенных шарнирами в треугольник (см. Рис. 2. 7, б). Установим, как может быть образована геометрически неизменяемая система, состоящая более чем из трех стержней, соединенных шарнирами.

Предварительно рассмотрим систему из двух стержней (Рис. 2. 9), лежащих на одной прямой и соединяющих узел С с двумя неподвижными точками А и В. Если разъединить стержни АС и ВС в точке С, то конец С стержня АС переместится по окружности т — т, а конец С стержня ВС — по окружности п — п. Эти окружности в точке С имеют общую касательную. Следовательно, если точка С одного из стержней получит весьма малое перемещение по перпендикуляру к АВ, то другой стержень не сможет воспрепятствовать

Рис. 2.9 Рис. 2.10

этому перемещению. Таким образом, рассматриваемая система является геометрически изменяемой, так как ее форма может меняться при неизменной длине стержней, т. е. при отсутствии деформаций ее элементов.

Систему с двумя стержнями, лежащими на одной прямой (Рис. 2. 9), в дальнейшем будем называть мгновенно изменяемой, так как она в следующее мгновение после малого смещения точки С по перпендикуляру к прямой АВ превращается в неизменяемую систему.

Иная картина получается, если стержни АС и ВС не лежат на одной прямой (Рис.2,10); в этом случае окружности т — тип — п не имеют общей касательной, а потому даже малое перемещение узла С невозможно без деформации стержней.-

Таким образом, всякий новый узел, добавляемый в процессе образования геометрически неизменяемой системы, может быть присоединен с помощью двух стержней, оси которых не должны лежать на одной прямой.

Следовательно, системы, подученные из шарнирного треугольника путем последовательного присоединения узлов, причем каждого двумя стержнями, не лежащими на одной прямой, геометрически неизменяемы, т. е. геометрическая структура их неизменяема. Такие системы (или фермы) называют простейшими в отличие от сложных, которые получают обычно в результате видоизменения простейших, в частности, с помощью замены одних стержней другими, или путем наложения одной системы на другую.

Ферма, состоящая только из треугольников, геометрически неизменяема. Любой шарнирный треугольник ее может рассматриваться как основной. Проверку геометрической неизменяемости простейших ферм можно производить и обратным путем, т. е. последовательно отбрасывая каждый узел и два стержня, прикрепляющих его к остающейся части фермы. Если в результате этого получится система в виде шарнирного треугольника, то рассматриваемая ферма геометрически неизменяема.

Перейдем теперь к вопросу о присоединении геометрически неизменяемых систем к земле посредством опор.

Наиболее часто сооружение (диск) опирается на две шарнирные опоры, одна из которых неподвижная, другая подвижная (Рис.2. 11, а). Такая связь сооружения с землей обеспечивает ему геометрическую неизменяемость. Не обязательно, чтобы два из трех опорных стержней объединялись одним общим шарниром; стержни геометрически неизменяемой системы могут и не иметь общих шарниров (Рис. 2.14, б).

Если все опорные стержни расположены так, что их направления пересекаются в одной точке О (Рис.2.12, а), то эта точка является мгновенным центром, вокруг которого система может совершать бесконечно малое вращательное перемещение (практически это перемещение может быть конечным, но малым). После такого

Рис.2. 11

перемещения все опорные стержни уже не будут пересекаться в одной точке и потому дальнейшие перемещения будут невозможны без деформации стержней.

Система, прикрепленная к земле подобным образом, обладает мгновенной подвижностью (мгновенной изменяемостью); такое расположение стержней недопустимо. Таким образом, прикрепление системы к земле с помощью трех стержней возможно лишь в том

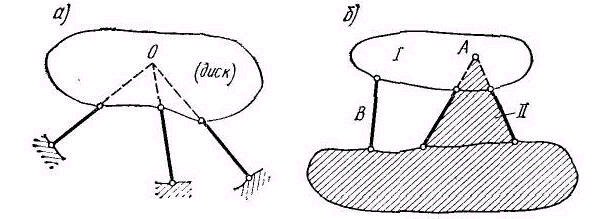
Рис.2.12 Рис.2.13

случае, когда осп этих стержней не пересекаются в одной точке и не параллельны друг другу.

Распространяя это положение на случай взаимного соединения двух любых геометрически неизменяемых систем (дисков), можно сформулировать следующее правило: два диска образуют геометрически неизменяемую систему, если они связаны между собой с помощью трех стержней, оси которых не пересекаются в одной точке и не параллельны друг другу.

Если в точке пересечения направлений любых двух из этих трех стержней поставить шарнир и соединить его с диском, то система не станет геометрически изменяемой, но это даст возможность рассматривать ее как состоящую из двух дисков / и //, связанных друг с другом одним общим шарниром А и стержнем В (Рис.2. 13, б).

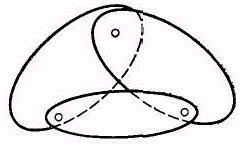
Рис.2.14

Следовательно, к. диску можно геометрически неизменяемо присоединить другой диск с помощью общего для обоих дисков шарнира и стержня, направление которого не должно проходить через этот шарнир.

Сочленение трех дисков в одну общую геометрически неизменяемую систему можно осуществить, соединив их в треугольник с помощью трех шарниров, не расположенных на одной прямой (Рис.2. 14), или с помощью шести стержней, как это показано на Рис.2. 15, так как каждый шарнир может быть заменен двумя стержнями, пересекающимися в его центре.

Система, изображенная на Рис.2. 16, мгновенно изменяема, так как точки пересечения осей стержней, связывающих каждую пару дисков, лежат на одной прямой.

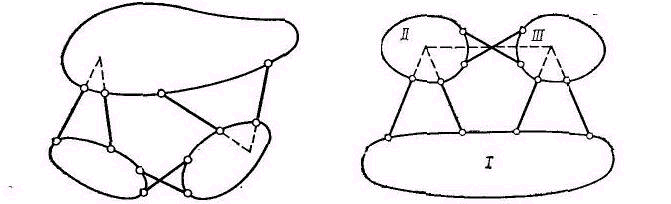
Рис.2.15 Рис.2.16

Итак, три диска, соединенных с помощью шести стержней так, что между каждой парой дисков установлено по два стержня, точки пересечения которых не лежат на одной прямой, представляют собой геометрически неизменяемую систему.

Из сказанного выше следует, что степень свободы W сооружения, состоящего из Д дисков, соединенных Ш простыми шарнирами и имеющего Со опорных стержней, может быть определена по формуле П. Л. Чебышева:

W = 3Д – 2Ш – С₀

Для определения числа Д необходимо предварительно отбросить все шарниры и опоры, а для определения числа Ш — все опоры.

Для шарнирно-стержневых систем (ферм), т. е. систем, состоящих из стержней, соединенных между собой по концам шарнирами (причем каждый стержень прикрепляется к соседним только двумя шарнирами), степень свободы может быть определена по более простой формуле:

W = 2У – С – С₀

где У — число узлов фермы; С — число внутренних стержней фермы;

Со — число опорных стержней.

Эта формула получена исходя из того, что каждый узел, как точка, имеет на плоскости две степени свободы, а каждый стержень, соединяющий два узла, или опорный эквивалентны одной связи, так как налагает на координаты этих точек единственное условие — постоянство расстояния.

Степень свободы системы, не имеющей опорных стержней, складывается из двух частей: степени изменяемости внутренней структуры системы и степени подвижности ее относительно основания, которая равна трем. Обозначая степень изменяемости структуры системы через И, можно записать

И=W – 3 – ЗД – 2Ш-3

или для шарнирно-стержневых систем

И=2У – С - 3.

Для системы, имеющей опорные стержни, не делают различия между степенью свободы и степенью изменяемости, рассматривая основание в качестве диска, связанного с сооружением опорными стержнями.

При определении степени свободы или степени изменяемости системы возможны следующие три качественно различных результата:

1. W > 0 или И > О — система структурно изменяемая, так как не имеет достаточного количества связей. Система, для которой W == 1 или И = 1, называется механизмом.

2. W == 0 или И = 0 — система обладает необходимым минимумом связей, чтобы быть неподвижной и неизменяемой.

3. W <; 0 или И < 0 — система имеет лишние связи. Аналитические условия W s^O или И -^ 0 являются необходимыми, но недостаточными для суждения о неизменяемости и неподвижности сооружения, так как эти характеристики зависят не только от числа связей, наложенных на диски, но и от их расположения.

Основная литература 1 [стр. 14-27], 2[стр.4-14]

Дополнительная литература 1[стр.13-27], 2[стр.15-15]

Контрольные вопросы:

1. Какая система называется геометрически неизменяемой

2. Какие виды опор используются в расчетных схемах сооружений

3. Какая опора называется шарнирно-подвижной

4. Какая опора называется шарнирно-неподвижной

5. Какая опора называется жесткой заделкой

6. Какие системы называются стержневыми

7. Какая система называется мгновенно-изменяемой

8. Аким образом можно соединить два диска при помощи трех стержней, чтобы получить геометрически неизменяемою систему

9. Как необходимо присоединять два диска при помощи шарнира и стержня. чтобы получить геометрически неизменяемою систему

10. Как можно соединить три диска при помощи трех шарниров, чтобы получить геометрически неизменяемою систему

11. Что называется степенью свободы системы

12. По какой формуле определяется число степеней свободы системы

13. Какие случаи возможны при определении степеней свободы системы

14. Как называется система у которой степень свободы больше нуля

15. Как называется система у которой степень свободы меньше или равна нулю

Тема лекции 3. Расчет статически определимых многопролетных балок

Из курса сопротивления материалов известны способы определения внутренних усилии, возникающих в поперечных сечениях однопролетных статически определимых балок, и построения эпюр этих усилий от действия на балки неподвижной нагрузки. Эти способы используются и в курсе строительной механики.

При определении значений внутренних усилий в балках будем пользоваться сформулированными ниже правилами.

Поперечная сила Q положительна, когда на левом торце правой части балки она направлена снизу вверх, а на правом торце левой части — сверху вниз.

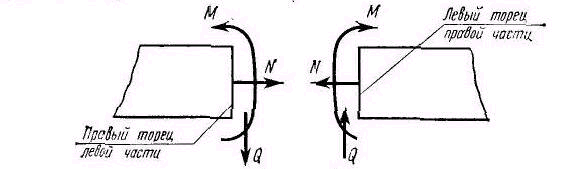
Рис.3. 1

Изгибающий момент М положителен, когда на левом торце правой части балки он направлен по часовой стрелке, а на правом торце левой части - против часовой стрелки.

При нагрузках, направленных не по нормали к оси балки (а под другим углом), в поперечных сечениях ее возникают кроме поперечных сил и изгибающих моментов также и продольные силы N. Продольная сила положительна, когда она вызывает растяжение, и отрицательна, когда она вызывает сжатие.

На рисунке показаны положительные направления поперечной силы, продольной силы и изгибающего момента в поперечном сечении балки. Из рисунка видно, что при положительном изгибающем моменте верхние волокна балки испытывают сжатие (укорочение), а нижние - растяжение (удлинение); положительная поперечная сила вращает каждую часть балки относительно другого ее конца по часовой стрелке.

При построении эпюр поперечных и продольных сил положительные значения ординат откладывают вверх от оси эпюры, а отрицательные - вниз; полезно указывать на отдельных участках эпюр знаки внутренних усилий. При построении же эпюры изгибающих моментов положительные значения их откладывают вниз от оси эпюры, отрицательные - вверх; в результате этого эпюры изгибающих моментов оказываются расположенными со стороны растянутых волокон балки.

З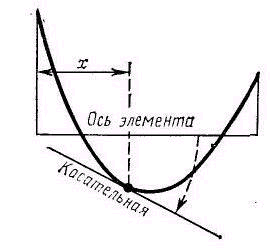нак поперечной силы можно установить с помощью эпюры изгибающих

Рис.3. 2

моментов, используя следующее правило: поперечная сила в данном сечении положительна, если для совмещения оси элемента с касательной к эпюре изгибающих моментов приходится ось элемента вращать по часовой стрелке. Вращение оси должно происходить всегда так, чтобы угол поворота не превосходил 90°.

Допустим, например, что требуется определить поперечную силу в сечении х элемента балки, эпюра изгибающих моментов для которого приведена на Рис.3.2. В этом случае для совмещения оси элемента с касательной к эпюре изгибающих моментов приходится ось элемента вращать по часовой стрелке (это вращение на чертеже показано штриховой стрелкой); следовательно, в рассматриваемом сечении поперечная сила положительна, так как для совмещения оси элемента с касательной нужно ось элемента повернуть по часовой стрелке (Рис.3. 2).

Поперечная сила Q равна (по величине и знаку) сумме проекций всех внешних сил, приложенных к левой части балки, на нормаль к ее оси, проведенную в рассматриваемом поперечном сечении, или сумме проекций (на ту же нормаль), взятой с обратным знаком, всех внешних сил, приложенных к правой части балки:

при этом проекции внешних сил на нормаль к оси балки положительны, когда они направлены снизу вверх.

Изгибающий момент М равен (по числовой величине и знаку) сумме моментов относительно оси г (проходящей через центр тяжести рассматриваемого поперечного сечения балки перпендикулярно плоскости действия внешних сил) всех внешних сил, приложенных к левой части балки, или сумме моментов, взятой с обратным знаком, всех внешних сил, приложенных к правой части балки:

при этом моменты внешних сил положительны, когда они действуют по часовой стрелке.

Продольная сила N равна (по числовой величине и знаку) сумме проекций всех внешних сил, приложенных к левой части балки, на ее ось или сумме проекций (на ту же ось), взятой с обратным знаком, всех внешних сил, приложенных к правой части балки:

при этом проекции внешних сил на ось балки положительны, когда они действуют справа налево.

Между эпюрами М и Q и нагрузкой, действующей на балку, существуют определенные зависимости. Эти зависимости позволяют проверять правильность эпюр и облегчают их построение. Они применимы не только для балок, но и для рамных систем, а потому имеют большое значение в строительной механике.

Основная зависимость имеет вид

Q = dM/dx,

т. е. поперечная сила равна первой производной от изгибающего момента по абсциссе сечения балки (теорема Журавского).

Аналогично между поперечной силой и интенсивностью нагрузки существует также дифференциальная зависимость

Q = dQ/dx.

Учитывая эти зависимости, можно сформулировать ряд положений:

1) участкам с восходящими (слева направо) ординатами эпюры М (т. е. с убывающими значениями М) соответствуют участки с отрицательными значениями Q, а участкам с нисходящими ординатами эпюры М - участки с положительными значениями Q;

2) чем круче касательная к эпюре М, тем больше абсолютное значение Q. Числовое значение поперечной силы равно «тангенсу» угла между этой касательной и осью балки;

3) в сечениях, где поперечная сила равна нулю, изгибающий момент максимальный или минимальный;

4) между сосредоточенными силами (если между ними отсутствует распределенная нагрузка) эпюра М ограничена прямой (в общем случае наклонной), а эпюра Q - прямой горизонтальной линией;

5) на участках балки с равномерно распределенной нагрузкой эпюра М ограничена параболой второй степени, а эпюра Q - наклонной прямой;

6) при распределенной нагрузке эпюра М обращена выпуклостью в ту сторону, в которую направлена эта нагрузка;

7) точка приложения сосредоточенных сил, перпендикулярных оси балки, соответствуют переломы в эпюре М и скачки в эпюре Q. Когда сила направлена вниз, то и скачок в эпюре Q при перемещении слева направо должен быть вниз; когда сила направлена вверх,

то и скачок должен быть вверх; величина скачка равна величине силы;

8) изменение числового значения величины изгибающего момента на каком-либо участке балки равно площади эпюры поперечных сил на этом участке (при условии, что на данном участке к балке не приложены внешние моменты);

9) изменение числового значения величины поперечной силы на каком-либо участке балки равно площади эпюры распределенной нагрузки q на этом участке.

В данной лекции рассматриваются способы определения усилий в поперечных сечениях многопролетных статически определимых балок от действия неподвижной нагрузок.

С подвижной нагрузкой приходится встречаться при расчетах мостов, кранов и других инженерных сооружений. Примерами такой нагрузки являются поезд, перемещающийся по железнодорожному мосту, кран, движущийся по подкрановой балке и др. и данная тема вынесена на самостоятельное изучение

Усилия в том или ином элементе сооружения (а также его деформации) зависят от положения подвижной нагрузки. Для определения расчетных величин усилий необходимо из всех возможных положений нагрузки выбрать такое, при котором рассчитываемый элемент будет находиться в наиболее неблагоприятных условиях. Например, при подборе размеров поперечного сечения какого-либо элемента фермы нужно заданную подвижную нагрузку расположить таким образом, чтобы в рассматриваемом элементе получить максимальное усилие. Такое положение нагрузки называется опасным. Каждому элементу фермы, каждому поперечному сечению балки и т. п. соответствует свое опасное положение подвижной нагрузки. Это относится не только к внутренним усилиям в элементах конструкций, но также и к опорным реакциям, прогибам и т. п.

Расчет сооружения на подвижную нагрузку в значительной степени облегчается возможностью применения принципа независимости действия сил, сущность которого заключается в том, что внутренние усилия, напряжения и деформации, вызванные воздействием на сооружение различных нагрузок, можно суммировать.

Если, например, на сооружение одновременно действуют две группы сил, то возникающее при этом усилие в любом элементе сооружения будет равно сумме усилий, возникающих в нем при действии каждой группы сил в отдельности.

Исследование действия на сооружение подвижной нагрузки заключается в построении линий влияния.

График, изображающий закон изменения какого-либо фактора (например, изгибающего момента в сечении) при передвижении по сооружению силы Р = 1, называется линией влияния этого фактора.

Линию влияния необходимо отличать от эпюры. Это по существу противоположные друг другу понятия. Действительно, ординаты эпюры характеризуют распределение изучаемого фактора (например, изгибающего момента) по различным сечениям балки при неподвижной нагрузке; ординаты же линии влияния, наоборот, характеризуют изменение фактора (например, того же момента), возникающего в одном определенном сечении при силе Р—1, перемещающейся по длине балки.

Среди статически определимых балочных систем наиболее распространены многопролетные шарнирно-консольные балки, идея и метод расчета которых были предложены в 1871 г. Г. С. Семиколеновым.

Многопролетной шарнирно-консольной балкой называется совокупность простых балок, имеющих консоли и связанных между собой промежуточными шарнирами. В зависимости от расположения шарниров могут применяться различные схемы, примеры которых приведены на Рис.3. 3, a—в.

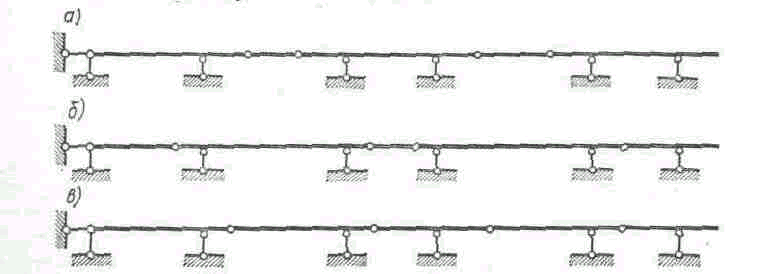
Рис.3. 3

Для структурной неизменяемости и число шарниров, введенных в пролеты, должно удовлетворять условию

Ш = С₀ – 3 (3.1)

где Со — число опорных стержней.

Из этого следует, что при крайних шарнирных опорах число шарниров в пролетах должно быть равно числу промежуточных опор.

Условие (3. 1) является необходимым, но недостаточным для структурной неизменяемости балки. Для обеспечения неизменяемости балки размещение шарниров в пролетах должно еще подчиняться следующим правилам:

1. В каждом пролете должно быть не более двух шарниров.

2. Пролеты с двумя шарнирами должны чередоваться с пролетами без шарниров.

3. Пролеты с одним шарниром могут следовать один за другим при условии, что один пролет остается без шарнира.

С точки зрения оптимизации конструкции шарниры целесообразно располагать так, чтобы наибольшие изгибающие моменты в пролетах и на опорах были равны между собой по абсолютному значению или находились в определенном соотношении.

Большим преимуществом шарнирно-консольных балок является то, что благодаря статической определимости в них не возникает

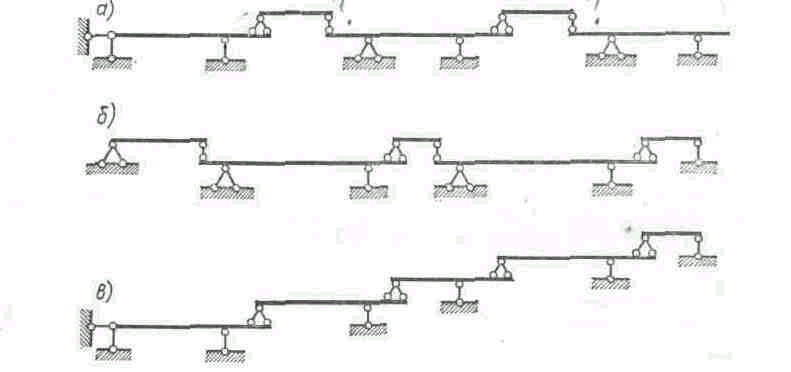
Рис.3. 4

усилий от теплового воздействия и осадок опор. Недостаток - меньшая жесткость по сравнению с неразрезными и конструктивные трудности при устройстве шарниров.

Для лучшего уяснения взаимодействия отдельных частей многопролетной шарнирно-консольной балки ее заменяют «поэтажной схемой». На Рис.3. 4 показаны этажные схемы, соответствующие балкам, изображенным на Рис.3. 3.

На схемах 3а и 3б отчетливо различается основная часть многопролетной балки, на которую опираются подвесные части, оказавшиеся на этажной схеме во втором этаже. На схеме 3 в все балки, кроме крайней левой, являются подвесными, причем каждая нижележащая балка служит опорой для всех вышележащих.

Нагрузка, действующая на основную часть балки, не передается на вышележащую подвесную; нагрузка же, действующая на подвесные части балки, передается на основную, которая служит опорой.

Расчет многопролетной шарнирно-консольной балки удобно вести по частям, начиная от самых «верхних» балок и последовательно переходя к нижележащим. При расчете нижележащих балок следует учитывать не только ту нагрузку, которая к ним непосредственно приложена, но и опорные давления от вышележащих балок, равные опорным реакциям последних, но имеющих обратное направление.

Расчет многопролетной шарнирно-консольной балки сводится к построению эпюр поперечных сил и изгибающих моментов, которые связаны между собой и с нагрузкой дифференциальными зависимостями, установленными Д. И. Журавским.

Эти принципы распространяются и на более сложные балочные системы.

Основная литература 1 [стр. 51-59], 2[стр.25-30]

Дополнительная литература 2 [стр.53-61]

Контрольные вопросы:

1. Что называется поперечной силой в произвольном сечении балки.

2. Что называется изгибающим моментом в произвольном сечении балки.

3. Какие внутренние силовые факторы действуют в сечениях многопролетной статически определимой балки.

4. Сформулируйте основные положения вытекающие из дифференциальных зависимостей между внешними и внутренними усилиями.

5. Что называется линией влияния.

6. В чем отличие эпюры от линии влияния

7. Алгоритм расчета многопролетной статически определимой балки на неподвижную нагрузку.

8. С какой балки по «поэтажной» схеме следует начинать расчет многопролетной балки.