
Методичка_Пределы (все части)
.pdf
lim |
sinπx |
= lim |
sinπ(t +1) |
|
(x −1)k |
t k |
|||
x→1 |
t→0 |
Ответ. k =1.
|
sinπ t |
= −lim sinπ t |
|
t |
∞, |
k >1 |
|||
= −lim |
lim |
= −1, |
k =1 |
||||||
t k |
t k |
||||||||
t→0 |
t→0 |
t |
t→0 |
|
|
|
|||
|
|
|
|
|
|
|
0, |
k <1 |
|
|
|
|
|
|
|
|
|||
Замечание. Метод сведения к определению 12, использованный при решении примера 46, требует вычислить предел, зависящий от параметра. Этой трудности можно избежать, применяяα ~ β метод эквивалентных преобразований, основанный на формуле (х) С( (х))k.
Определение 13. βВ случаях, когда используетсяα одна из формул (8), степенная функцияαС( (х))k, эквивалентная функции (х), называется главной частью функции (х) при соответствующем стремлении аргумента.
|
Пример 47. Найдем при х→0+ порядок малости и главную часть3 |
|||||||||||||||||||||||||||||||
функции α(х)= |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1−cos x |
|
|
|
~ |
|
|
|
|
|
|
|
|
k |
|
1 |
|
|
|
|
|||||||||||||
|
Решение. |
Мы знаем, что |
|
1 cosх~х2/2 |
при |
х→0. Отсюда, |
извлекая |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
x |
|
|
|
|
|
|
|
|
||||||||
квадратный корень, получаем |
|
− |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
(с учетом положительного |
||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1−cos x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
знака х). Последнее выражение имеет вид С(β(х))x , где β(х)=х, С= |
|
|
|
, k=1. |
||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||
2 |
||||||||||||||||||||||||||||||||
|
Ответ. Порядок малости k=1; главная часть |
|
|
|
|
. |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
Если в предыдущем примере рассмотреть стремление х→0-, порядок |
|||||||||||||||||||||||||||||||
малости снова будет равен 1, а главная часть изменит знак (почему?) |
|
|||||||||||||||||||||||||||||||
x→ |
При использовании метода |
эквивалентных |
преобразований бывает |
|||||||||||||||||||||||||||||
|
|
|
|
, а (х) – |
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α |
|
|
|
∙γ |
||||||
полезна следующая теорема. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Теорема |
7. |
Пусть |
(х) |
|
представима |
|
в |
виде |
(х)=f(х) |
|
|
|
(х), где |
||||||||||||||||||
lim f (x) = A ≠ 0;∞ |
|
|
|
бесконечно большая (или бесконечно малая) при |
||||||||||||||||||||||||||||
х→ |
. Тогда при этомγ стремлении аргумента |
|
|
|
(х) А |
(х). |
|
|
|
|
|
|
|
|||||||||||||||||||
|
Упражнение. Докажите эту теорему. |
|
α |
|
~ ∙γ |
|
|
|
|
|
|
|
||||||||||||||||||||
|
Пример |
48. |
Найдем |
порядок малости |
|
и |
главную |
часть |
|
|
|
функции |
||||||||||||||||||||
α(х)= |
x2 cos x |
при х→0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1+ x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
3 В условии подразумевается, что β(х)=х, поскольку при указанном стремлении х→0+ функция α(х) – бесконечно малая.
7

|
Решение. |
α= |
Перегруппируем формулу, выделив бесконечно |
малый |
|||||
множитель: |
(х)= cos x x2 |
)= cos x |
непрерывна2 |
|
|
||||
lim |
|
= f (0) |
1+ x |
. Функция f(х |
cos1x+ x2 |
в нуле, |
поэтому |
||
x→0 |
f (x) |
|
|
1. По теореме 7 получаем |
1+ x x |
~ x . |
|
|
|
Ответ. Главная часть: x2 . Порядок малости k=2.
Теорема 1 (о связи бесконечно больших и бесконечно малых),
сформулированная в п. 3.1., может быть уточнена следующим образом. |
|
|
||||||||||||||||||||||||||||
Теорема 8. При х→ |
β( х) тогда |
(х) является бесконечно малой порядка |
||||||||||||||||||||||||||||
|
|
|
|
|
|
и только |
тогда, |
когда |
|
функция |
1 |
|
||||||||||||||||||
малости |
k относительно функция α |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
α(x) |
|
|||||||||||||||||
является бесконечно большой порядка роста k относительно |
|
|
1 |
|
. |
|
|
|||||||||||||||||||||||
|
β(x) |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Пример 49. Вычислим при x → π |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||||
|
а. |
порядок роста функции A(x) = 3 |
|
|
(относительно |
|
|
|
); |
|
|
|||||||||||||||||||
|
tg x |
|
|
|
|
|
||||||||||||||||||||||||
|
x − |
π |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
б. |
порядок малости функции α(x) = 3 |
|
|
(относительно x − π ). |
|
|
|||||||||||||||||||||||
|
ctg x |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
2 |
|
|
||
Решение. |
|
а. |
Сделаем |
замену |
t = x − |
|
|
и |
|
|
|
рассмотрим |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
A(x(t)) = 3 |
tg(t + |
π ) |
= −3 |
|
= − |
3 |
cost |
|
. При t→0 A(x(t)) |
− |
1 |
|
, т.е. порядок роста |
|||||||||||||||||
ctg t |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||
A(x(t)) |
|
|
2 |
|
|
3 |
sin t |
|
|
|
|
|
|
|
3 t |
|
|
|
|
|
|
|
|
|
|
|||||
|
равен 1/3. Тот же самый порядок роста |
~ |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
A(x) . В самом деле, мы можем переписать предыдущую эквивалентность,
вернувшись к переменной х: |
A(x) ~ − |
|
1 |
|
. |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||
3 |
x − π2 |
|
|
||||||||||||||||||||||||
б. |
|
Действуя |
|
|
|
|
аналогично |
|
пункту |
а, |
получаем |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
~ |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
π |
|
|
|
|
|
|
|
|
sin t |
|
|
|
|
|
|
|
|
|
|||||
a(x(t)) |
|
ctg(t |
|
|
|
|
|
tg t = |
π |
|
−3 |
|
t . |
|
(Или, вернувшись |
к старой |
|||||||||||
|
|
2 ) |
|
|
|
3 |
cost |
|
|
||||||||||||||||||
|
= 3 |
|
+ |
|
|
= −3 |
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
переменной, |
|
α(x) |
|
−3 x − |
2 |
|
). И здесь k=1/3. Разумеется, вторую выкладку |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
можно было бы |
заменить ссылкой на теорему 8. |
|
|
||||||||||||||||||||||||
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Ответ. k=1/3.
Переформулируем правило 9 из предыдущего пункта для задач о поиске главной части.
8

Правило 10. Главная часть произведения (частного) двух бесконечно малых или бесконечно больших равна произведению (частному) главных частей исходных функций.
Пример 50. Найдем главную часть функции f(х)= 1−cos35x2 при х→0+.
arcsin x
Решение. Мы не можем сразу определить, является данная функия
бесконечно малой или бесконечно большой, т.к. lim |
f (x) = |
0 |
|
. Однако, это не |
x→0+ |
|
0 |
|
|
препятствует поиску главной части методом эквивалентных преобразований:
f(х)= |
(1−cos x)(1+cos x +cos2 x) |
= (1+cos x +cos2 x) |
|
1−cos x |
. |
||||||||
|
|
|
|||||||||||
|
|
arcsin x5 2 |
|
|
|
|
|
|
|
arcsin x5 2 |
|||
Предел первого сомножителя равен 3. По теореме 7 и правилу 10 |
|||||||||||||
|
|
f(х) |
|
|
1−cos x |
|
|
x2 / 2 |
|
|
3 1 |
1/ 2 |
|
|
|
3 |
|
|
|
3 |
|
= |
|
. |
|||
|
|
arcsin x5 2 |
|
x5 / 2 |
|||||||||
Последнее |
выражение |
и |
|
|
|
|
2 x |
|
|||||
|
есть искомая главная часть. Функция f(х) |
||||||||||||
|
|
|
~ |
|
|
~ |
|
|
|
|
|
|
|
оказалась бесконечно большой с порядком роста k=1/2. |
|||||||||||||
Ответ. f(х)~ |
3 1 1/ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 x . |
|
|
|
|
|
|
|
|
|
|
|
||
В примерах 42, 43 обсуждалась проблема, связанная с вычитанием бесконечно малых. Сейчас мы можем разобраться в этом вопросе более
основательно.
Теорема 9. При х→ (f−g=o(f) f~g ).
Теорема 9 справедлива как для бесконечно больших, так и для бесконечно малых функций.
Контрольный вопрос. Дайте словесную формулировку теоремы 9: а) для бесконечно малых; б) для бесконечно больших. Необходимую терминологию см. в п. 6.1.
Следствие 1. Главная часть разности (или суммы) бесконечно малых с различными порядками малости совпадает с главной частью функции с
меньшим порядком малости. |
|
– |
х2 |
~ |
|
Например, при х→0 разность х |
х. |
||||
Следствие 2. Главная часть |
|
|
|
||
|
разности (или суммы) бесконечно больших с |
||||
различными порядками роста совпадает с главной частью функции с
большим порядком роста.
Например, при х→∞ разность х– х2 ~−х2.
Чтобы не перепутать формулировки следствий 1 и 2, полезно задавать себе проверочный вопрос:
Чему примерно равна разность:1) одной десятой и одной тысячной? 2) десяти и тысячи?
9

Замечание. Если в сумме или разности присутствует слагаемое, которое не является ни бесконечно большим ни бесконечно малым, ему можно условно приписать нулевой порядок.
α(х)= 0,01x2 |
+ln(ex |
+1) +sin x |
при х→∞. |
||
Пример 51. |
Найдем |
порядок малости и главную часть функции |
|||
|
|
1 |
|
|
|
Решение. Исследуем знаменатель дроби, который является бесконечно большой~ функцией. Очевидно, что для первого слагаемого k1=2. Далее, ln(ex+1) ln(ex)=х, поэтому k2=1. Приписывая синусу k3=0 и используя следствие 2, получаем, что главная часть знаменателя равна 0,01х2. Отсюда немедленно следует ответ.
Ответ. Главная часть: 100x2 . Порядок малости k=2.
Правило 11. Большинство задач анализа бесконечно малых и бесконечно больших можно свести к вычислению главных частей.
Пример 52. |
Даны функции f(х)= |
x3 |
+ xsin x |
и g(х)= |
x2 |
+ x +1 |
при х→∞. |
|||
|
x + 3 |
|
|
|
x + 2 |
|
||||
|
x |
|
||||||||
Требуется:
а) Определить, являются ли эти функции бесконечно малыми или бесконечно большими.
б) Найти их главные части и порядки малости (роста). в) Сравнить функции f и g.
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вида ∞ |
|
||||
1) Найдем |
главную |
часть |
|
функции |
f. |
Поскольку |
это дробь |
, |
|||||||||||||||
исследуем числитель и знаменатель отдельно. |
|
|
|
|
|
∞ |
|
||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||
Функция |
xsin x |
|
|
не |
– |
является |
|
бесконечно |
большой |
в |
|
смысле |
|||||||||||
|
|
|
|
|
|
|
|
π |
4 |
|
|
xsin x = 0 может выполняться |
|||||||||||
определения 7. (В самом деле, равенство |
|||||||||||||||||||||||
для сколь угодно больших x= k, |
|
k .) Поэтому условно припишем ей |
|||||||||||||||||||||
порядок 0. Функция х3 |
|
|
бесконечно большая порядка 3; следовательно, |
||||||||||||||||||||
это и есть главная часть числителя . |
|
|
|
|
1> 1 . Главная |
|
|
|
|||||||||||||||
Порядок |
роста |
|
знаменателя |
равен 1, |
т.к. |
|
часть |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
х2. |
|
знаменателя – его первое слагаемое х. По правилу 10 находим f(х) |
|
|
|
||||||||||||||||||||
2) Найдем |
главную |
|
|
часть |
функции |
g. |
Рассуждения, |
аналогичные |
|||||||||||||||
|
|
|
|
~ |
|
|
|||||||||||||||||
предыдущим (проведите |
их сами!), дают g(х)~ х. |
|
|
|
|
|
|
|
|||||||||||||||
|
3 |
|
|
|
|
|
|
|
|||||||||||||||
4 Рассуждая более аккуратно: lim |
x + xsin x |
= lim(1+ |
sin x |
) =1. |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
x→∞ |
|
x3 |
|
x→∞ |
|
|
x2 |
|
|
|
|
|
|
|
10 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

3) Из результатов пунктов 1) и 2), с учетом теоремы 6, вытекают ответы на все оставшиеся вопросы. А именно:
• функции f и g – бесконечно большие;
• lim |
f |
= lim |
x2 |
= ∞. Таким образом, g(х)=о(f(х)). |
|
|
|||
x→∞ g |
x→∞ x |
|
||
Ответ. а) Бесконечно большие; б) f(х)~х2, k1=2; g(х)~ х, k2=1; в) g(х)=о(f(х)).
Замечание. Следует помнить, что не у всех бесконечно больших и бесконечно малых функций имеются главные части. Для таких функций
правило 11 неприменимо. |
|
|
|
|
|
|
|
|
Пример 53. Покажем что у функции lnx при х→+ |
нет порядка роста и |
|||||||
главной части. |
∞ |
|
|
ln x |
|
∞ |
|
|
Решение. Следуя определению 12, |
запишем предел |
lim |
|
|
= |
|
при |
|
|
k |
|||||||
|
|
|
x→+∞ x |
|
|
∞ |
|
|
любом k>0. Раскроем неопределенность по правилу Лопиталя (правило 6):
lim |
ln x |
= lim |
(ln x)′ |
= lim |
1/ x |
= lim |
1 |
= 0 . Таким обазом |
lnx=o(xk) при |
||||
xk |
|
(xk )′ |
|
|
|||||||||
x→+∞ |
|
x→+∞ |
|
x→+∞ kxk −1 |
x→+∞ kxk |
|
|
||||||
любом k>0. |
|
|
|
|
|
|
|
|
|||||
Пример 54. Вычислите |
самостоятельно главную |
часть фукции |
|||||||||||
|
|
|
4 |
|
|
|
|
х→+∞, отвечая последовательно на вопросы: |
|||||
f(х)= |
|
|
x |
|
при |
||||||||
|
|
|
|
|
|
||||||||
x3 + 2x +ln x |
|||||||||||||
1)Какого типа функции стоят в числителе и знаменателе? (Бесконечно большие.)
2)Чему равна главная часть числителя? (Самому числителю, т.е. х1/4.)
3)Чему равна главная часть подкоренного выражения в знаменателе? Указание. Используйте результат примера 53 и теорему 9. (х3.)
4)Чему равна главная часть f(х)?
x1/ 4 |
|
1 |
− |
6 |
1 |
5 / 4 |
|
||
|
|
|
= x |
4 |
|
4 |
= |
|
|
|
3 / 2 |
|
|
|
|
||||
x |
|
|
|
|
|
x |
|
|
|
1 5 / 4
Ответ. x .
Задачи для самостоятельной работы
Вычислить пределы, используя основные эквивалентности.
1) |
lim |
|
|
1−e2x2 |
|
|
|
; |
|||||
arcsin x • ln(1+ x) |
|||||||||||||
|
x→0 |
|
|
||||||||||
2) |
lim(x |
2 |
+ x |
3 |
|
1 |
|
|
|
||||
|
|
)arctg |
|
|
|
|
; |
||||||
|
|
|
|
|
|
||||||||
|
x→∞ |
|
|
|
|
x2 |
|
|
|||||
3) |
lim(5 |
|
|
|
|
|
|||||||
32x5 |
|
+16x4 |
−2x); |
||||||||||
|
x→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
11

4) |
lim(3 |
x+1 |
|
πx |
|
|
−9) tg |
2 |
; |
||
|
x→1 |
|
|
|
|
5) |
3 |
x5 |
|
|
+sin(x4 ) |
|
||
lim |
|
|
|
|
|
|
. |
|
|
|
|
|
+1) |
−2ln x) |
|||
|
x→+∞ x4 (ln(x |
2 |
|
|||||
Найти главные части и порядки малости функций при х→0.
6)α(x) = 1+1 x −1;
7)α(x) = tg(
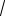 x + 2 −
x + 2 − 
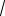 2);
2);
8)α(x) = arctg x12 (53 x −1);
x −1);
9)α(x) = sin(x + π6 ) − 12 .
|
|
|
11) |
|
A(x) = 9x2 |
|
+1 − x |
при х→ |
|
∞; |
|
|
|
|
|
|
||||||||||||||||||||||
|
Найти главные части и порядки роста функций. |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
при х→∞; |
|
|
|
|
|
|
|
|
|
||||
|
|
|
10) |
|
A(x) = |
|
|
x + |
|
|
|
|
x + |
|
|
x |
|
|
при х→+ |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞; |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
15x5 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
12) |
|
A(x) = |
|
|
9x6 −5e−x |
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
arcsin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
13) |
|
A(x) = |
|
|
|
|
|
|
x |
|
при х→1+0; |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
x −1 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
A(x) = sin |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
14) |
|
x |
при х→0+ . |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
16) |
|
|
|
e |
x −1 |
|
|
|
при∞;х |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
Существуют ли главные части у следующих функций? |
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
15) |
|
α(x) = sin x |
|
при х→ |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
17) |
|
α(x) = cx |
(c >1) |
при х→- ∞; |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
18) |
|
|
|
|
x |
|
|
|
|
при х→0+ .∞; |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
A(x) = loga x |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
A(x) = cx |
(c |
>1) |
|
|
|
|
|
|
→+ |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Ответы. 1) -2; |
2) |
|
|
; |
|
|
3) 1/5; |
4) -18ln3/ ; 5) 0; |
6) –x, k=1; 7) |
x |
|
|
|
k=1; |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞3 |
|
|
|
|
|
|
|
|
|
|
|
π |
|
2 |
2 |
|
|
|||
|
π ln 5 |
|
1/ 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||||||
8) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
2 |
|
|
|
x |
|
|
, k=1/3; 9) |
|
|
|
x , k=1; |
10) |
|
|
x , k=1/2; 11) |
2x , k=1; 12) |
5x |
|
, k=2; |
|||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|||||||||||||||||||||||||||||
|
π |
|
|
|
1 |
|
|
|
|
|
|
1 1/ 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
13) |
|
• |
|
|
|
|
|
, k=1; |
14) |
|
|
|
, k=1/6; |
15)-18) Не существуют. |
|
|
|
|
|
|||||||||||||||||||
2 |
|
x −1 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
7.НЕПРЕРЫВНОСТЬИРАЗРЫВЫ
7.1Определения непрерывности и их геометрический смысл.
Основное определение и некоторые свойства непрерывности уже были сформулированы в п. 3.1. Напомним это определение.
Определение (VIP). Функция f(x) непрерывна в точке x = a , если
lim f (x)= f (a).
x→a
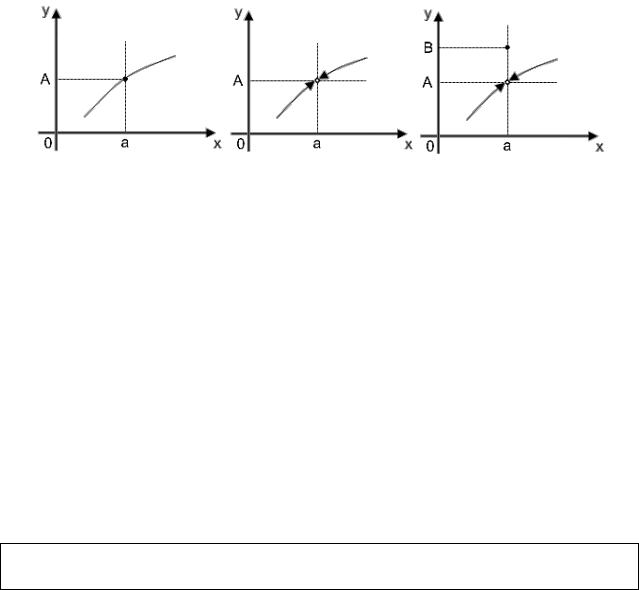
Фактически, сопоставление предела и значения функции в одной и той же точке было начато нами еще раньше – при обсуждении рисунков 7, 8, 9.
Рис.7 Рис.8 Рис.9 Интуитивно ясно, что непрерывна только функция на рис. 7. Точнее
говоря, она непрерывна во всех точках области определения. Функции на
рис. 8 и 9 разрывны при |
x |
|
a. О таких случаях также говорят: функция |
||||||||||||||
теряет непрерывность или терпит разрыв. |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
→ |
|
|
|
|
переформулировки |
|||
Для более детального обсуждения приведем две |
|
||||||||||||||||
основного определения непрерывности. |
|
|
|
|
|
|
|
||||||||||
Определение 14а. Функция f(x) непрерывна в точке x = a , если |
для |
||||||||||||||||
любого |
ε > 0 |
найдется |
δ > 0 , такое что |
для всех |
|
x , удовлетворяющих |
|||||||||||
условию |
|
x −a |
|
<δ , выполняется неравенство |
|
f (x)− f (a) |
|
< ε . |
|
|
|
||||||
|
|
|
|
|
|
|
|||||||||||
Или в |
символах: ε>0 δ>0: |x-a|<δ |f(x)−f(а)|<ε. |
|
|
|
|
|
|||||||||||
Назовем |
|
|
приращением |
аргумента величину |
|
x=x-a, приращением |
|||||||||||
функции – величину |
∆ |
у=f(x)−f(а)=f(а+ х)−f(а). Будем∆рассматривать |
∆ |
у как |
|||||||||||||
функцию от |
|
|
x. |
|
|
|
∆ |
|
|
|
|
|
|
||||
Определение 14б. Функция f(x) непрерывна в точке x = a |
, если |
у – |
|||||||||||||||
|
|
|
∆ |
|
|
|
|
|
|
|
|
|
|
||||
бесконечно малая при |
|
x |
0. |
|
|
|
|
|
|
|
|
∆ |
|||||
∆ →
Формулировка 14б раскрывает суть понятия непрерывности: малые
изменения аргумента приводят к малым изменениям функции.
Пример 55. Докажем, что функция у=х непрерывна в любой точке x=a.
1
Доказательство. Для любого ε > 0 найдется δ = ε , такое что для всех x , удовлетворяющих условию x −a <δ , после замены обозначений получим
неравенство y(x) − y(a) < ε .
=Пример 56. Докажем, что функция у=sinх непрерывна в любой точке
xa.
∆. ∆ Прежде всего, установим зависимость между приращениями у и x:
∆y = sin x −sin a = 2sin |
x −a |
cos |
x + a |
= 2sin ∆x cos(a + |
∆x) . |
|
|
|||||||||
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
2 |
|
2 |
|
2 |
|
|
2 |
|
|
Далее |
заметим, |
|
что | |
y |= 2 | sin |
x −a |
| • | cos |
x + a |
|≤ 2 | sin ∆x |≤ 2 | |
∆x |=| ∆x | . |
|||||||
|
2 |
2 |
||||||||||||||
Отсюда следует, что |
|
у 0 при |
x |
0. |
|
|
2 |
2 |
||||||||
|
|
|
sinα~α. |
|
|
|||||||||||
α |
, |
|sinα|≤|α|, |
|
но |
|
|
∆ → |
|
|
|
|
|||||
Замечание. В |
|
∆ → |
|
|
|
|
|
|
|
|
||||||
|
|
|
доказательстве использованы элементарные неравенства |
|||||||||||||
|cos |
|≤1 |
|
|
|
|
|
не эквивалентность |
|
|
Дело в том, |
что при |
|||||
обосновании первого замечательного предела (а значит, и всех его следствий) используется непрерывность тригонометрических функций.
Никакое доказательство не должно содержать ссылок (прямых или косвенных) на доказываемое утверждение.
Заменив в основном определении двусторонний предел односторонним,
получим определение односторонней непрерывности.
Определение 15. Функция |
называется непрерывной слева (непрерывной |
справа) в точке x = a , если lim |
f (x)= f (a) ( lim f (x)= f (a)) . |
x→a−0 |
x→a+0 |
Графики функций, непрерывных слева и справа в точке а, приведены на рисунках 18 и 19 соответственно. (Оба этих рисунка получены из рис.17
путем доопределения f(a).)
Определение 16. Функция называется непрерывной на промежутке,
если она:
1) непрерывна в каждой внутренней точке промежутка;
2
2)односторонне непрерывна в каждой граничной точке, входящей в промежуток.
7.2. Классификация точек разрыва
Определение 17. Точка x=a называется точкой разрыва функции, если эта функция определена в проколотой окрестности точки a, но не является непрерывной в этой точке.
Контрольный вопрос.
Является ли x=0 точкой разрыва для функций: а) lgx; б) tgx; в) сtgx?
Определение 18. Точками разрыва первого рода функции f(x) называют
такие |
точки |
разрыва, |
в |
которых |
односторонние |
пределы |
A = lim |
f (x), B = lim f (x), существуют и конечны. В частности, |
при А=В |
||||
x→a−0 |
|
x→a+0 |
|
|
|
|
говорят≠ об устранимом разрыве, а неустранимый разрыв первого рода (где
А В) называют скачком.
Примеры устранимых разрывов приведены на рис. 8 и 9, примеры скачков – на рис. 17, 18, 19.
Определение 19. Точками разрыва второго рода функции f(x) называют такие точки разрыва, в которых хотя бы один из односторонних пределов
A = lim f (x), B = lim |
f (x), не существует или бесконечен. |
||
x→a−0 |
x→a+0 |
|
|
Примеры функций, имеющих разрыв второго рода: |
|||
1) |
Функция, изображенная на рис. 12; |
||
2) |
Функция 1/х при x |
→ |
|
0 (нарисуйте график самостоятельно); |
|||
3) |
Функция |
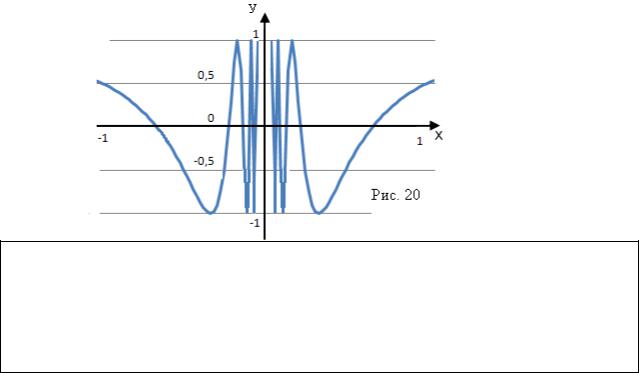
cos(1/→х) при x 0 (график на рис. 20) |
|
Исследование непрерывности и разрывов функции включает в себя:
1)Нахождение точек разрыва.
2)Исследование характера каждой точки разрыва.
Это исследование позволяет построить эскиз графика функции в окрестности точек разрыва в соответствии с геометрической интерпретацией односторонних пределов.
3
Для элементарных функций первая часть исследования делается на основе теоремы 3. Из нее вытекает
Правило 12. Точками разрыва элементарной функции являются точки, выколотые из области определения, и только они.
Вторая часть исследования – поиск односторонних пределов в каждой точке разрыва. Отметим, что такой расчет далеко не всегда связан со сложными вычислениями.
Пример 57. Исследуем точки разрыва функции f (x) = |
21/ x |
|
21/ x −2 |
||
|
Решение. 1) Сразу видим точку разрыва а=0. Другую точку определяем из уравнения 21/ x −2 = 0. Отсюда а=1.
2) Для а=0
A = lim |
|
21/ x |
|
= |
|
2−∞ |
|
= |
|
|
0 |
= 0; |
||
21/ x −2 |
2 |
−∞ − |
2 |
0 |
−2 |
|||||||||
x→−0 |
|
|
|
|||||||||||
B = lim |
|
21/ x |
= lim |
|
2t |
|
=1. |
|
||||||
|
21/ x −2 |
|
|
−2 |
|
|||||||||
x→+0 |
|
|
t→+∞ 2t |
|
|
|
||||||||
Вывод: В точке а=0 функция имеет |
||||||||||||||
скачок. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для а=1 сразу видим, что оба односторонних предела бесконечны. Т.е., здесь мы имеем разрыв 2-го рода.
Чтобы построить эскиз графика, следует учесть знаки А и В. Для этого заметим, что
21/ x −2 > 0 |
при х |
(0;1) и |
21/ x −2 < 0 при |
|||||||
х |
|
(1;+ ). Поэтому |
|
|
|
|
||||
|
∞ |
21/ x |
|
2 |
|
|
|
|||
|
|
A = |
lim |
|
|
= |
|
|
= +∞; |
|
|
|
|
x→1−0 |
21/ x −2 |
|
+0 |
|
|
|
|
|
|
B = |
lim |
21/ x |
= |
2 |
|
= −∞. |
|
|
|
|
21/ x −2 |
−0 |
|
||||||
|
|
|
x→1+0 |
|
|
|
||||
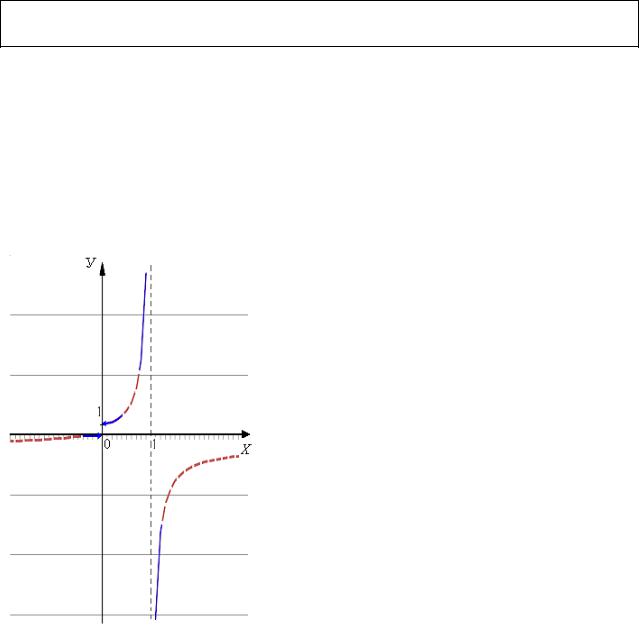
Эскиз графика в окрестности точек разрыва – синие и фиолетовые линии на рис. 21.
Рис. 21 (Для большей наглядности мы изобразили график целиком.)
Не всегда функция задается одним и тем же правилом (формулой) на всей области определения. Такие функции называются составными. Точки, в которых происходит смена правила, называются точками склейки. В этих точках возможны как сохранение непрерывности, так и ее потеря.
|
2 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример 58. Исследуем непрерывность функции |
f (x) = x |
|
x |
|
|
≤ 2 . |
||
|
|
|
||||||
|
x + 2, |
|
|
x |
> 2 |
|||
|
|
|
|
|
|
|
||
4
