Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный технический университет им. H.Э.Баумана

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Методичка_Пределы (все части)

.pdf

Скачиваний:

122

Добавлен:

23.03.2016

Размер:

8.48 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 73 4 5 6 7 > Следующая >>>

Т6) Основные формулы приведения сведем в таблицу.

Функция Аргумент

α +

α −

α ±π

sin

cosα

-cosα

-sinα

cos

-sinα

sinα

-cosα

-ctgα

tgα

формуламиНаприм , sin(α-π/2)=-cosα.

Комбинируя

эти

формулы с

ctg

- tgα

ctgα

Т3), можно

получить более общие формулы

приведения. Например,

sin(

π/2-α)=

α-π/2)=

α)=

cos

α.

-sin(

-(-cos

Схема Горнера. Часто возникает необходимость разложить на множители многочлен n-й степени, имеющий корень с. Надеемся, что читатель умеет это делать, если n =2. При произвольном n рекомендуем использовать схему Горнера, состоящую в следующем.

	Пусть		Pn (x) = a0 xn + a1 xn−1 + + an−1 x + an ,				и число с	– корень этого
многочлена. Запишем данные в таблицу.
	a0	a1		an−1	an	Пустые клетки в нижнем ряду таблицы
						заполним слева	направо	по формулам:
с						заполним слева	направо	по формулам:
						a0 =b0, a1+b0c=b1, a2 +b1c=b2 и т.д.		При расчете без

ошибок должно получиться bn = 0 . Остальные числа – коэффициенты

многочлена	Qn−1 (x) = b0 xn−1 + +bn−2 x +bn−1 ,	связанного с	Pn (x)
соотношением Pn (x) = (x −c)Qn−1 (x) .			с=-1
Пример.	P4 (x) = x4 + 4x3 + 6x2 + 4x +1	имеет корень	с=-1

(проверьте!) Вычисления по схеме Горнера дают таблицу:

		1	4	6	4	1
(Более подробно: 1=1,	-1	1	3	3	1	0
(Более подробно: 1=1,	4+1(	-1)=3,		6+3(-1)=3, 4+3(-1)=1, 1+1(-1)=0.)

Это означает, что P4 (x) = (x +1)(x3 +3x2 +3x +1) .

Упражнение. Продолжите расчет и разложите P4 (x) на сомножители первой степени.

Ответ. P4 (x) = (x +1)4 .
3.3. Простейшие приемы вычисления пределов
Пример 6. Вычислим пределы: а)lim	(x2 +1)2x		; б) lim((x + 2)(1−	1) +	2	) .
Пример 6. Вычислим пределы: а)lim	x −1		; б) lim((x + 2)(1−	1) +		) .
x→2	x −1		x→0	x	x		(x2 +1)2x
Решение. а) Заметим, что в точке x = 2		элементарная функция			f (x)=		(x2 +1)2x
Решение. а) Заметим, что в точке x = 2		элементарная функция			f (x)=		x −1
непрерывна по теореме 3. И следовательно,		lim f (x)= f (2)= 20 .					x −1
непрерывна по теореме 3. И следовательно,		lim f (x)= f (2)= 20 .
		x→2

б) Функция не является непрерывной при x = 0, т. к. она в этой точке не определена. Однако, при всех x ≠ 0 справедливы алгебраические тождества:

		4) lim	sin x	= lim sin x		(x + 2)(1− 1) +	2	= x + 2 −1− 2	+ 2 = x +1.	Последняя
		x→∞	x		x→∞	x	x	x	x
						функция уже является непрерывной при x = 0. Поэтому
lim((x + 2)(1−			1) +	2) = lim(x +1) =1.
x→0			x	x	x→0
	Ответ. а) 20; б) 1.
	3.4. Правила вычисления пределов, содержащих различные
неопределенности.
0	При вычислении предела функции могут появиться неопределенности вида
0	∞				и т.д.	Слово «неопределенность»			означает,	что результат
	,	,[∞ −∞]			и т.д.	Слово «неопределенность»			означает,	что результат
0	∞

вычислений не описывается каким-то универсальным правилом, а зависит от конкретной формулы.

Пример 7. Рассмотрим четыре предела:

1) lim

; 2) lim

;

3) lim Cx

, C ≠ 0;

4) lim

x(sin x + 2)

. Попытка вычислить эти пределы

x→∞

x→∞ x

x→∞

по теореме 2 приведет во всех случаях к неопределенности ∞

. Однако, после

очевидных сокращений мы легко найдем:

∞

x(sin x + 2)

= lim x

= C ≠ 0; 4) lim

= lim(sin x + 2)

1) lim

= ∞;

2) lim

= lim

= 0; 3) lim

x→∞

x→∞ 3

x→∞

не существует, т.к. при росте x значения синуса колеблются от -1 до 1.

Отметим (пока без доказательства) что при замене в знаменателях х на х+1 ни один из четырех результатов не изменится, хотя ситуация станет не столь очевидной. Обсуждение примера 7 будет продолжено в п. 6.2.

Запомните, что результаты

= 0, 1 = ∞,

(+∞ + ∞) = +∞

не содержат в себе

∞

неопределенности.

ПРАВИЛО 1.

(x)

= ∞

Если при

х

возникла

неопределенность lim

, необходимо в

(x)

x→∞

∞

числителе и

знаменателе вынести за скобку х в максимальной степени (если

∞

это возможно) и сократить дробь.

Пример 8. Вычислим A = lim

(3x − 2)2 (4x +3)2

x→∞

8x4 +1

(4x +

lim(3x −1)2

lim(4x +3)2

∞ ∞

∞

Решение.

(3x − 2)

x→∞

→∞

A = lim

lim(8x

+1)

∞

x→∞

∞

x→∞

Получили неопределенность, от которой можно избавиться, используя правило 1. Из кажд ого множителя в числителе и знаменателе вынесем x в максимальной степени.

	1			2			3	2					1	2					3	2					1	2						3	2
	1						3	2
x 3 −					x 4 +
x 3 −					x 4 +				x	2	3	−			x	2							3	−						4	+
	x						x		x		3	−	x		x			4 +	x			lim	3	−	x		lim			4	+	x			9 16
A = lim	x						x	= lim					x						x		=	x→∞			x		x→∞					x		=	9 16	=18
A = lim						1		= lim					4					1			=								1					=	8	=18
x→∞	x	4	8			1		x→∞				x	4					1											1						8
				+									8		+									lim			8	+	x
				+		x4							8		+		x4							lim			8	+
						x4											x4							x→∞

Ответ. A =18 .

Замечание. В дальнейшем часть преобразований, связанных с использованием теорем о пределах, будем выполнять в уме.

ПРАВИЛО 2. (о пределе дробно-рациональной функции)

Если при ха возникла неопределенность lim			Pm (x)	= 0 , то необходимо в
Если при ха возникла неопределенность lim			Qn (x)	= 0 , то необходимо в
		x→a	Qn (x)	0
числителе и знаменателе выделить множитель			(x − a) и сократить дробь (т.к.
Pm (a)= 0 и Qn (a)= 0 , то оба многочлена такой множитель содержат).

Пример 9. Вычислим A = lim	x2 + x −3	.
Пример 9. Вычислим A = lim		.
x→3	x2 −9

Решение. Подставим в функцию x = 3 и выясним, приведет это к ответу или к неопределенности.

A = lim	x2	+ x −3		9		= ∞ .
				=
	x	2	−9		0
x→3

Получили результат, который не является неопределенностью.

Ответ. A = ∞.

Пример 10. Вычислим A = lim

x3 −3x + 2

x3 − x2 − x +1

x→1

Решение. Подставим в функцию x =1

x3 −3x + 2

A = lim

− x

− x +1

x→1

Получили неопределенность, от которой можно избавиться, применив правило

2. Выделим в

числителе

и знаменателе множитель (x −1).

Для этого

можно

использовать схему Горнера (или деление «уголком»).

Числитель:

x3 + 0x2 −3x + 2 = (x −1)(x2 + x − 2)

Знаменатель можно разложить следующим образом:

x3 − x2 − x +1 = x2 (x −1)−(x −1)= (x −1)(x2 −1)

Теперь

A = lim

(x −1)(x2 + x − 2)

= lim

+ x − 2

(x −1)(x

−1)

−1

x→1

Опять после подстановки

получили неопределенность. Еще раз воспользуемся

правилом 2.

Числитель является квадратным трехчленом вида ax2 +bx + c = a(x − x1 )(x − x2 ), один корень которого x =1 известен. Используя теорему Виета, а именно то, что

x1 x2 = ac = −2 , найдем второй корень x = −2 .

Получим

A = lim

(x −1)(x + 2)

= lim

x + 2

(x −1)(x +1)

x +1

x→1

Ответ.

A =

Пример 11. Вычислим A = lim

−

x −3

x→3 x2 −9

Решение. Подставим в функцию x = 3 .

A = lim

−lim

= [∞ −∞].

x2 −9

x −3

x→3

Получили неопределенность. Преобразуем данное выражение в рациональную дробь, приведя его к общему знаменателю.

A = lim

6 −(x +3)

= lim

3 − x

−

−9

x→3

−(x −3)

−1

1 .

Применяя правило 2, получим A = lim

= lim

= −

(x −3)(x +3)

x +3

x→3

Ответ.

A = −

1 .

ПРАВИЛО 3. (для функций, содержащих радикалы)

Если при вычислении предела функции, содержащей иррациональность,

получается неопределенность, от которой нельзя избавиться, применяя правила 1 и 2 ,то необходимо преобразовать задачу так, чтобы стало возможным применение правил 1 и 2. Для этого можно применить следующие способы:

1)ввести новую переменную, после чего все корни извлекаются;

2)тождественно преобразовывая выражение, дополнить его до одной из формул А1-А3, применение которой избавит неопределенность от корней.

Пример 12. Вычислим A = lim 3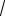x − 2 −1 .

x→3 4 x − 2 −1

Решение. Подставим в функцию x = 3 .

A = lim 4		x − 2 −1		= 0	.
	3			0
			−1
x→3		x − 2

Получили неопределенность, избавиться от которой, используя правило 2 нельзя из-за наличия корней. Следуя правилу 3, сделаем замену x − 2 = t12 , которая

позволит избавиться одновременно от обоих корней. При этом t = 12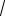x − 2 . При стремлении х к 3 новая переменная t →12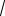3 − 2 =1.

Получим	A = lim t	4	−1	=	0	.
		3
	t→1 t		−1		0

Неопределенность, естественно, осталась, но появилась возможность применить правило 2. Разложим числитель и знаменатель новой рациональной дроби на множители и упростим выражение.

A = lim

(t −1)(t +1)(t 2

+1)

= lim

(t +1)(t 2

+1)

4 .

t→1

(t −1)(t 2 +t +1)

t→1

t 2 +t +1

(Мы использовали формулы a2

−b2 = (a −b)(a +b), a3 −b3 = (a −b)(a2 + ab +b2 )).

Ответ.

A = 4 .

−3

Пример 13. Вычислим A = lim

x +5

x→4

−5x + 4

Решение. Подставим в функцию

x = 4 .

A = lim

x +5

−3

x→4

−5x + 4

Получили неопределенность, от которой можно будет избавиться по правилу 2 только после того, как мы уберем корень в числителе. Для этого умножим одновременно числитель и знаменатель на выражение, сопряженное числителю,

т.е. на (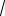x +5 +3). При этом будет построена формула А1: a2 −b2 = (a −b)(a +b).

(

−3)(

+3)

+5 −9

x − 4

A = lim

x +5

= lim

lim

= lim

−5x + 4)( x +5 +3)

x +5 +3

−5x + 4

x→4

−5x + 4 x→4

x→4

Теперь используя правило 2, получим

A = 1 lim

x − 4

= 1 lim

1 1 =

(x − 4)(x −1)

6 x→4

6 x→4 x −1

6 3 18

Ответ.

A =

(

− x); б) lim (

− x).

Пример 14. Вычислим a) lim

−3x + 7

x2 −3x + 7

x→+∞

x→−∞

Решение. а) При непосредственной подстановке в выражение x = +∞ получаем

− lim x = [+ ∞ −∞]

- неопределенность не рассмотренного ранее

A = lim

−3x + 7

x→+∞

типа.

Так как функция содержит корень,

необходимо от него избавиться.

Для

этого умножим и разделим ее на сопряженное выражение.

( x2 −3x +7 − x)(

+ x)

A =

lim

x2 −3x +

= lim

x2 −3x + 7 − x2

= lim

−3x + 7

∞

x2 −3x + 7 + x

x→+∞

∞

Хотя новое выражение опять содержит корень, теперь можно избавиться от получившейся неопределенности, применив правило 1.

−3 +

−3 + x

= − 3 .

A = lim

= lim

1− 3 +

1− 3 + 7

x→+∞

б) Этот пример1 по виду очень похож на пример а), но здесь никакой неопределенности нет∞: + ∞ −(−∞) = +∞ + ∞ = +∞ .

Ответ. а) − 32 ; б) + .

Пример

15. Вычислите

самостоятельно

A = lim x2 (3

− x),

отвечая

x3 +5

последовательно на вопросы.

x→∞

Решение.

1) Что получается при непосредственной подстановке x = ∞, ответ

или неопределенность?

(неопределенность [∞(∞ −∞)])

Какое правило можно применить, чтобы избавиться от этой

неопределенности?

(правило 3)

Чтобы избавиться от корня, входящего в выражение, необходима замена

переменной или дополнение до формулы и какой именно?

(дополнение до формулы a3 −b3

= (a −b)(a2 + ab +b2 ) )

Преобразуйте выражение выбранным способом.

(

A = lim

5x2

)

(x3 +5)2 + x3

x→∞ 3

x3 +5

+ x2

Что

получается

при непосредственной

подстановке

x = ∞

в новое

выражение?

(неопределенность вида ∞

)

∞

6) Какое правило можно применить, чтобы избавиться от этой неопределенности?

(правило 1)

7) Преобразуйте выражение выбранным способом и вычислите предел. Ответ. A = 53 .

Задачи для самостоятельной работы. Вычислите следующие пределы.

A = lim

3x4

+5x −3

A = lim

x2 −7x +10

, 3)

A = lim

− 27

x2 − 25

x→∞

(2x +1)2

x→5

x→729

6 x −3

A = lim (x +

), 5)

A = lim(

− x), 6)

−3

x + 6

+ 6x +1

x3 + 2x2

A = lim

x→−∞

3 , 2)

x→∞

2 ,6)

2 .

x→3

x +1 − 2

Ответы. 1)

, 3)

27 , 4) −3, 5)

1 Пределы, где результат зависит от знака бесконечности, к которой стремится аргумент х, называются односторонними пределами на бесконечности. Они подробно рассмотрены в главе 4

3.5. Первый замечательный предел

ПРАВИЛО 4. (для выражений, содержащих тригонометрические функции)

Если при вычислении предела выражения, в котором содержатся тригонометрические функции, появляется неопределенность, то для избавления от нее необходимо свести задачу к вычислению первого замечательного предела, а именно

					lim sinα =1, где			α =α(x)	(1)
					α→0 α
Пример 16. Вычислим A = lim sin 2x .
					x→0	x − 4
Решение. При непосредственной подстановке в выражение x = 0 получаем
	sin 2x		0
A = lim	x − 4	=			.
A = lim		=	−	4	.
x→0			−	4
Результат не содержит неопределенности.
Ответ.	A = 0 .
Пример 17. Вычислим A = lim sin Cx								(С 0).
					x→0	x
Решение. При непосредственной							подстановке в выражение		x = 0 получаем
Решение. При непосредственной								≠
A = lim sin Cx		= 0			. Получили неопределенность и, так как данное выражение
x→0	x	0

содержит тригонометрическую функцию, воспользуемся правилом 4 и выделим

первый замечательный предел.

Преобразуем A так, чтобы появилась дробь sinαα , где α = Cx .

A = lim sin Cx		= lim C sin Cx		= C lim sin Cx	= C 1 = C .
x→0	x	x→0	Cx	x→0 Cx
Ответ.	A = C .

Пример 18. Вычислим A = lim sin 2x .

x→∞ x

Решение. При непосредственной подстановке в выражение x = ∞ получаем

	sin 2x	sin ∞
A = lim		=		.
	x		∞
x→∞

Предел числителя не существует (см. замечание 3 в главе 2). Однако, заданный в условии предел, не содержит неопределенности, так как в нем ограниченная величина делится на бесконечно большую. Таким образом, получаем A = 0 .

Ответ. A = 0 .

Пример 19. Вычислим A = lim sin 3x .

x→0 sin 4x

Решение. При непосредственной подстановке в выражение x = 0 получаем

A = lim sin 3x	=	0		- неопределенность и, так как данное выражение содержит
x→0 sin 4x		0

тригонометрическую функцию, воспользуемся правилом 4 и выделим первый замечательный предел и в числителе, и в знаменателе.

Роль α

в числителе играет 3x , а в знаменателе 4x .

A = lim sin 3x

sin 3x

1 3x

= 3 .

= lim

sin 4x

1 4x

x→0

sin 4x

x→0

3 .

Ответ.

A =

Пример 20. Вычислим A = lim

1−cos x .

x→0

Решение.

При

непосредственной

подстановке

в выражение x = 0

получаем

A = lim

1−cos2

x = 0

-неопределенность

и, так как

данное выражение

содержит

x→0

тригонометрическую функцию, воспользуемся правилом 4 и выделим первый замечательный предел. Для этого преобразуем выражение следующим образом.

A = lim

1−cos x

= lim

−cos x)(1+ cos x)

= lim

−cos2 x

lim

= lim

sin 2

x→0

x2 (1+ cos x)

x→0

1+ cos x

x→0

sin x 2

lim

x→0

Ответ. A = 12 .

Пример 21. Вычислите A = lim tgx самостоятельно, отвечая последовательно на

x→0 x

вопросы.

Решение. 1) Что получается при непосредственной подстановке x = 0, ответ

или неопределенность?	(неопределенность типа	0	)
		0

2) Какое правило можно применить, чтобы избавиться от этой неопределенности? (правило 4)

3) Выделите в данном выражении первый замечательный предел и найдите

ответ.			(используйте tgx = sin x		).
Ответ.	A =1.			cos x
Ответ.	A =1.
Пример 22. Вычислим A = lim arcsin x .
			x→0	x
Решение.		При	непосредственной подстановке в выражение x = 0 получаем
A = lim arcsin x		= 0	-неопределенность. Но ни к одному из рассмотренных правил
x→0	x	0

данное выражение не подходит. Так как воспользоваться известными правилами не позволяет наличие функции arcsinx, заменим ее новой переменной.

A = lim arcsin x

arcsin x = t

= t → 0

= lim

=1. (правило 4)

sin t

x→0

t→0

lim

Ответ.

A =1.

x = sin t

t→0

При решении примеров 17 и 20-22 были получены следствия первого замечательного предела, которые часто встречаются при вычислении более сложных пределов. Этими следствиями далее мы будем пользоваться как табличными.

Следствия первого замечательного предела.

lim

2) lim tgα =1

α→0 sinα

α→0

lim arcsinα =1

4) lim arctgα

(2)

α→0

lim1−cosα =

6) lim sin Cx

= C

α→0

α2

x→0

Пример 23. Вычислим A = lim sinπx .

x→2

x − 2

Решение. При непосредственной подстановке в выражение

x = 2

получаем

A = lim sinπx

= 0

-неопределенность

и,

так как

данное выражение

содержит

x→2 x − 2

тригонометрическую функцию, воспользуемся правилом 4 и выделим первый замечательный предел. Но в данном пределе аргумент синуса не является нужной величиной α(x)→ 0 , т.к. πx → 2π ≠ 0 . Значит, пока выделить первый

замечательный предел мы не можем. Введем новую переменную такую, чтобы она стремилась к нулю.

x − 2 = t	= lim sinπ(t + 2)		= lim sin(π t + 2π)		= lim sin(π t)		= 0	.
A = t → 0	= lim sinπ(t + 2)		= lim sin(π t + 2π)		= lim sin(π t)		= 0	.
	t→0	t	t→0	t	t→0	t	0

x = t + 2

К новому выражению можно применить правило 4 при α = π t .

И окончательно получим

A = lim sin(π t) π

=1 π = π .

Ответ. A = π .

x→2

πt

Задачи для самостоятельной работы.

Вычислите следующие пределы.

7) A = lim tgπx

8) A = lim tgπx ,

9) A = lim

2sinπx

x→0 sin x

x→1 sin x

x→2

x2 − 4

3)tg πx ,

1−sin 2x

12) A = lim tg x −sin x .

10) A = lim(x −

11)

A = lim

x→3

(π − 4x)

x→0

x→4

Ответы. 7) π ,8) ∞,9)

π ,10) −

,11)

1 , 12)

1 .

3.6. Второй замечательный предел.

До сих пор остались не разобранными примеры, содержащие показательные

функции, логарифмы, а также пределы вида lim(f (x))ϕ(x). Следующее правило (без

x→

номера) описывает простейшие ситуации такого типа, не содержащие неопределенностей.

Если lim f (x)= A ≠ {0,1}

и limϕ(x)= B , то lim(f (x))ϕ(x) = AB .

x→

Запомните, что при

c (0;1) (1;+∞)

выражения вида

+ ∞,

c >1

c+∞ =

< c <1

c−∞ =

не содержат неопределенности.

c+∞

Пример 24. Вычислим A = lim

2x +3

x→0 x

−

+∞

= 0

Решение. A = lim

−

2x +3

x→0 x

Полученный результат не содержит неопределенности и дает ответ на вопрос. Ответ. A = 0 .

В рассматриваемом случае могут появиться неопределенности типа [00 ][, ∞0 ][, 1∞ ] . В данном разделе будет рассмотрена неопределенность только

одного типа [1∞ ]. Остальные требуют использования производных и будут разобраны в главе 5.

ПРАВИЛО 5. (для сложно-показательных функций)

Если lim(f (x))ϕ(x) = [(1)∞ ], то для избавления от неопределенности необходимо
x→
свести задачу к вычислению второго замечательного предела, а именно
lim (1+1/ x)x = e	(3а)
x→∞

или

lim(1+α)α = e , где α =α(x). (3б)

α→0

Легко заметить, что формула (3б) сводится к формуле (3а) заменой α =1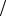x .

Менее заметно различие между формулой (3а) и определением числа е в п. 1.3. Это различие – не просто в букве, обозначающей аргумент. Дело в том, что х может быть вещественным числом любого знака2, a n – только натуральным числом.

Вообще говоря, если некоторое свойство выполняется для вещественных чисел, то оно верно и для чисел натуральных. А вот обратное справедливо далеко не всегда. Вывод формулы (3а) из определения числа е – трудная теорема.

Пример 25. Вычислим A = lim x +3 x .

x→∞ x

2 За исключением чисел из отрезка [-1;0].

<<< < Предыдущая 1 23 / 73 4 5 6 7 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
09.02.2015895.51 Кб40Методичка ПТМ №27.docx
#
27.04.2019115.11 Кб4Методичка Технологическая карта.docx
#
13.08.20191.13 Mб24Методичка Численные методы решения дифур.doc
#
09.02.20152.47 Mб74МЕТОДИЧКА.doc
#
09.11.20195.63 Mб14Методичка_(версия_для_печати).doc
#
23.03.20168.48 Mб122Методичка_Пределы (все части).pdf
#
23.03.2016158.48 Кб24Методичка_Пределы_1_Оглавл.pdf
#
23.03.2016373.58 Кб8Методичка_Пределы_2_Предел_послед_и_Опр_пред_функц.pdf
#
23.03.2016312.03 Кб11Методичка_Пределы_4_Сравн_Функц.pdf
#
09.02.20156.67 Mб119Методички по физике 2 курс.doc
#
05.05.2019224.26 Кб0МетодУк_пр_зан_2012.doc