
Методичка_Пределы_2_Предел_послед_и_Опр_пред_функц
.pdf
1.ПРЕДЕЛПОСЛЕДОВАТЕЛЬНОСТИ
1.1Понятие числовой последовательности.
Числовая последовательность – это функция натурального аргумента
an = f (n), n N.
Ее графиком на плоскости XOY является множество изолированных точек, абсциссы которых есть натуральные числа n = {1,2,3.....}.
То есть, числовая последовательность представляет собой бесконечное множество чисел, связанных общим законом, который задается общим элементом an .
Пример 1. Дана функция an = (3−n1)−n1n натурального аргумента. Вычислим
несколько первых ее значений.
Решение. Зададим конкретное значение аргумента n и подставим его в выражение an .
При n=1 получим a1 = |
(−1)1 |
|
= − |
1 |
, при n=2 |
a2 |
= |
(−1)2 2 = 2 |
, при n=3 |
a3 |
= − |
3 |
|
3 1−1 |
2 |
8 |
|||||||||||
|
|
|
|
|
3 2 −1 5 |
|
|
|
|||||
и т.д.
Например, при n=10 получим a10 = 1029 .
Последовательности, описываемые простыми правилами, удобно задавать перечислением начальных членов.
Пример 2. Задано несколько элементов числовой последовательности:
a1 = − 12 , a2 = 14 , a3 = −16 .
Найдем выражение общего элемента an как функции аргумента n.
Решение. Легко заметить, что при n=1, 2, 3 an = 21n . Чередование знаков: минус, плюс, минус и т.д. – описывается с помощью множителя (−1)n .
Окончательно получаем ответ: an = (−21n)n .
Запомните, что чередование знаков плюс, минус, плюс и т.д. – описывается с помощью множителя (−1)n+1 . Последовательность четных чисел можно записать как 2n, нечетных – как (2n-1), n N .
1.2 Предел числовой последовательности.
Как ведет себя последовательность при росте n? Следующие три примера показывают, что имеется три принципиально различных типа поведения.
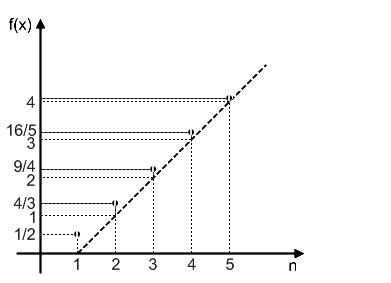
Первый из них: an = nn+2 1 . Вычислим несколько первых элементов этой последовательности и проанализируем, как они изменяются с ростом номера n.
1
При n=1 a1 |
= |
1 , при n=2 |
a2 = 4 |
=11 |
, при n=3 a3 = 9 |
= 2 1 , при n=4 |
a4 |
= |
16 |
= 3 |
1 |
||||
|
|
2 |
3 |
3 |
|
|
4 |
4 |
|
|
5 |
|
|
5 |
|
, при n=5 a5 = |
25 |
= 4 1 и т.д. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Очевидно, что чем больше номер n, тем больше значение an . |
|
|
|
|
|
|
|||||||||
Нетрудно заметить, что an = (n −1) + |
1 |
|
, и при очень больших n поведение |
an |
|||||||||||
n +1 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
похоже на поведение последовательности n-1. Вывод: an → ∞ при n → ∞. (См. рис.1)
Рис.1
Рассмотрим теперь вторую последовательность, где bn = (−1)n . Другими
словами, это: -1, 1, -1, 1, … Последовательность колеблется, оставаясь ограниченной.
Контрольный вопрос. Нарисуйте график последовательности bn . |
|
|
|||||
Последовательности, которые ведут себя, как an |
или |
bn , |
называются |
||||
расходящимися. |
|
|
(−1)n 2 |
|
|||
Наконец, рассмотрим третью |
последовательность, где |
cn = |
. Вычислим |
||||
|
|||||||
несколько первых ее элементов. |
|
|
|
n |
|
|
|
=1 , при n=3 c3 = − 2 , при n=4 |
|
|
1 , при n=5 |
||||
При n=1 c1 = −2 , при n=2 c2 |
c4 |
= |
|||||
|
3 |
|
|
|
|
2 |
|
c5 = − 52 и т.д.
Очевидно, что чем больше номер n, тем значение cn меньше, и при возрастании n эти значения становятся все ближе к числу 0. (См. рис.2)
2
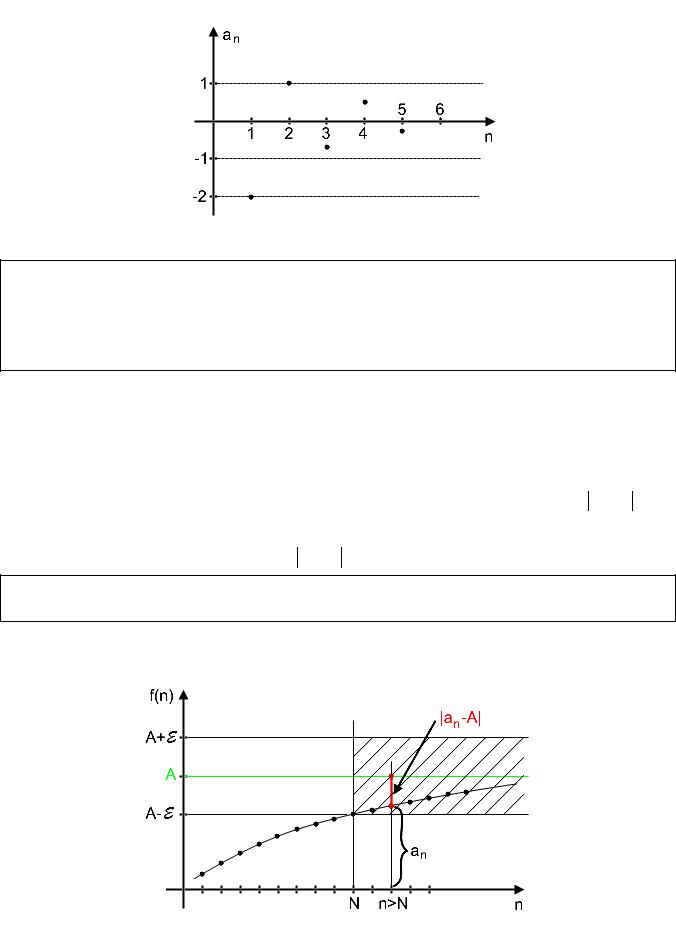
Рис.2
Последовательность, у которой все элементы с достаточно большими номерами приближенно равны одному и тому же числу, называется сходящейся. Число, к которому приближаются значения элементов последовательности при возрастании номера n, называется пределом этой последовательности.
Следующее определение формализует понятия «приближенно равны» и «достаточно большие номера».
Определение 1. Число А называется пределом числовой последовательности
{an }, то есть A = lim an , если для любого, сколь угодно малого, ε > 0 найдется
n→∞
такой номер N(ε), что для всех n > N(ε) будет выполняться неравенство an − A < ε . В логических символах определение 1 можно записать следующим образом:
def
A = lim an = ε > 0 N(ε): n > N(ε) an − A > ε .
n→∞
Последовательность, имеющая предел, называется сходящейся, не имеющая предела – расходящейся.
Рассмотрим графическую иллюстрацию определения 1(См. рис.3).
Рис.3
3

На оси ординат выбрана произвольным образом ε -окрестность точки А.1 На координатной плоскости ей соответствует заштрихованная полоса шириной
2ε .
Точки с ординатами an при возрастании номера n располагаются все ближе к
прямой y = A. И |
для |
любого ε > 0 |
найдется такой |
номер |
N, |
что все |
точки, |
|||
соответствующие |
элементам |
последовательности с |
n > N , |
окажутся |
внут и |
|||||
заштрихованной полосы. Обозначение N |
(ε) подчеркивает, что выбор номера |
|||||||||
N зависит от выбора числа |
. |
|
|
|||||||
Напомним, |
что |
наε |
|
рис.1 |
изображены |
элементы |
расходящейся |
|||
последовательности. Нетрудно убедиться, что в этом случае при любом предположительно выбранном А, и для любых ε и N, найдется бесконечно много точек, оказавшихся вне соответствующей полосы шириной 2ε при n > N .
Пример 3. Найдем число А, являющееся пределом числовой последовательности с общим элементом an = n2+n1 , и пользуясь определением,
убедимся в правильности ответа.
Решение. Вычислим несколько первых элементов данной последовательности.
n =1 a1 =1, n = 2 a2 = 43 =113 , n = 3 a3 = 64 =112 , n = 4 a4 = 85 =153 , n = 5 a5 = 106 =1 23 , n = 6 a6 = 127 =175 .
Проанализировав результат, видим, что элементы при больших значениях n
увеличиваются |
и |
все |
|
они ограничены так, что |
1 < an < 2.Появилось |
|||||||||
предположение, что искомое число А равно 2. |
|
|
|
|
||||||||||
С другой |
стороны, |
an можно тождественно преобразовать |
следующим |
|||||||||||
образом: |
|
|
|
|
|
|
|
|
|
|
||||
an = |
2n |
= |
2(n +1)−2 |
= 2 − |
2 |
|
. |
|
|
|
|
|||
|
|
n +1 |
|
|
|
|
||||||||
|
n +1 |
n +1 |
|
|
|
2 |
|
|
|
|||||
Теперь очевидно, что при возрастании номера дробь |
|
уменьшается и при |
||||||||||||
n +1 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
n → ∞ она стремиться к нулю. В таком случае, при достаточно больших значениях n элементы последовательности приближаются к числу 2, то есть искомый предел
А=2, или lim an = 2 .
n→∞
Докажем, что это действительно так, пользуясь определением 1 предела числовой последовательности.
Число А=2 будет пределом данной последовательности, т.е. lim |
2n |
= 2 , если |
|||||||
|
|
||||||||
для любого ε > 0 |
|
|
|
|
N |
n→∞ n +1 |
|
||
найдется такой номер |
, что для всех |
n > N будет |
|||||||
|
2n |
|
|
(ε) |
|
|
|
|
|
выполняться неравенство |
− 2 |
< ε . |
|
|
|
|
|||
n +1 |
|
|
|
|
|||||
1 Детальное обсуждение понятия окрестности – в следующей главе.
4

Вопрос заключается в том, найдется ли номер N(ε), необходимый для выполнения последнего неравенства?
Преобразуем это неравенство следующим образом, учитывая, что n+1>0:
|
|
|
|
|
|
2n |
− 2 |
|
< ε |
|
|
2n − 2n − 2 |
|
< ε |
2 |
|
|
< ε |
n + |
1 > |
2 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n +1 |
|
|
n +1 |
ε |
|
|
||||||||||||||||||
|
|
|
|
|
|
n +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
В |
итоге |
|
получаем |
|
n > |
2 |
|
−1. |
Именно |
для таких |
|
|
номеров n |
выполняется |
|||||||||||||||||||||
|
|
|
ε |
|||||||||||||||||||||||||||||||||
|
|
|
ε≥ |
|
|
|
|
|
|
|
|
|
|
. (В |
|
|
|
ε |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
ε(ε)=1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
неравенство, следующее из определения 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
При |
|
1 |
возьмем N |
|
|
|
|
|
Если (0;1), то в качестве номера N(ε) выберем |
||||||||||||||||||||||||||
целую |
часть числа |
|
2 |
|
|
|
|
частности, |
если выбрать |
ε = 0,01, то номер |
||||||||||||||||||||||||||
|
|
− |
1 |
|
||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
2 |
|
|
=199 , а если |
ε = 0,03, то |
|
|
2 |
|
|
|
|
= 65.) |
|
|
|
|
|
|
|
|||||||||||||||
N1 |
= |
|
|
−1 |
N2 = |
|
|
|
−1 |
|
|
|
|
|
|
|
||||||||||||||||||||
0,01 |
0,03 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
И теперь видим, что для любого ε > 0 можно найти такой номер N(ε), что для |
|||||||||||||||||||||||||||||||||||
всех |
n>N(ε) |
|
будет |
выполняться |
неравенство |
|
2n |
− 2 |
|
< ε . |
Таким |
образом, из |
||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n +1 |
|
|
|
|
|
|
|
||
определения 1 для данной последовательности следует, что ее пределом является число А=2.
Угадать значение предела А и аккуратно проверить выполнение определения 1 можно только в тех случаях, когда последовательность задана простейшими формулами. В более сложных примерах применяются правила вычисления пределов, которые подробно рассмотрены в главе 3. Некоторые из этих правил использованы в решении следующего примера.
Пример 4. Выясним, является ли сходящейся последовательность с общим
элементом an = (
 n +1 −
n +1 − 
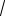 n )
n )
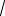 n .
n .
Решение. Числовая последовательность является сходящейся, если существует
предел A = lim an .
n→∞
Чтобы вычислить этот предел или убедиться в том, что он не существует, преобразуем an тождественно следующим образом.
lim an = lim( |
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
( |
|
|
− |
|
|
|
)( |
|
|
|
|
+ |
|
|
) |
|
|
|
|
(n +1−n) |
|
|
|
||||||||||||||||||
|
|
|
|
− |
|
|
|
|
|
|
= lim |
|
n +1 |
|
|
n |
|
|
n +1 |
|
n |
|
n |
|
= lim |
n |
= |
|||||||||||||||||||||||||||||
n +1 |
n |
|
n |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
( |
|
n +1 + n ) |
|
|
|
|
|
|
|
n +1 + n |
|||||||||||||||||||||||||||||||||||||||
n→∞ |
n→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
n→∞ |
|
|
|
|
|
|
|
|
|
|
n→∞ |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
= lim |
|
|
n |
|
|
|
= lim |
|
|
|
|
|
n |
|
|
|
|
|
= lim |
|
|
|
|
|
|
|
|
|
|
= |
, |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
n→∞ |
n +1 + n |
|
|
n→∞ |
|
|
1+ |
1 |
|
|
|
n→∞ |
1 |
+ |
1 |
|
+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
т.к. очевидно, что при n → ∞ |
дробь |
1 |
→ 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ответ: данная числовая последовательность сходится к пределу А=1/2.
1.3Число е.
Вычислим (с помощью компьютера или калькулятора) значения
элементов последовательности an = (1+1/ n)n при некоторых n.
5

n |
1 |
2 |
3 |
4 |
5 |
10 |
11 |
12 |
|
|
|
|
|
|
|
||
an |
2 |
2,25 |
2,37037 |
2,44140 |
|
2,59374 2,60420 2,61303 |
||
|
|
|
|
|
|
|
|
|
n |
99 |
100 |
365 |
1000 |
10 000 |
|
|
|
an 2,70468 2,70481 2,71456 2,71692 2,71814
Мы видим, что, во-первых, эта последовательность возрастает. Во-вторых, рост постепенно замедляется, и даже при очень больших n элементы последовательности не превосходят числа 2,72.
Можно строго доказать (см., например [Морозова]), что данная последовательность сходится. Ее предел называется эйлеровым числом, или числом е, в честь математика Л.Эйлера (1707-1783).
e = lim(1+1/ n)n = 2,71828...
n→∞
Число е – иррациональное. Мы ограничились пятью цифрами после запятой в его разложении в бесконечную десятичную дробь.
Роль числа е и в математической теории, и в прикладных расчетах колоссальна. Например, рассмотрим процесс роста банковского вклада. Банк устанавливает по вкладам годовую ставку Р% и выплачивает проценты n раз в году. Если начисленные в середине года проценты присоединяются ко вкладу, и на них тоже начисляются проценты (так называемые сложные проценты), то к
концу года первоначальная сумма вклада увеличится в (1+100P n)n раз.
Нетрудно заметить сходство этой формулы с формулой из определения числа е. Позже мы покажем (см. далее пример 25 и
замечание к нему), что lim(1+ |
P |
)n = eP /100 . |
|
100n |
|||
n→∞ |
|
На практике это означает, что при достаточно частых выплатах (например, при ежемесячных, т.е. при n=12) рост вклада за год легко рассчитать умножением первоначальной суммы на , делая при этом очень незначительную ошибку. Дальнейшее увеличение периодичности выплат (банк мог бы выплачивать проценты не ежемесячно, а ежедневно) не приведет к существенному увеличению дохода вкладчика.
Натуральный логарифм. Логарифм числа b>0 по основанию е называется натуральным логарифмом, и для него используется
специальное обозначение2 |
def |
ln b = loge b . |
Задачи для самостоятельной работы.
2 В иностранной математической и в переводной экономической литературе также встречается обозначение log b без указания основания логарифма.
6
1. Даны несколько первых элементов числовой последовательности. Составьте выражение общего элемента an .
а)1, 3 , |
5 |
, |
|
7 |
|
...... |
|
|
Отв. an = |
2n −1 |
|
|
|
|||||||||
9 |
16 |
|
|
|
|
|
||||||||||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
n2 |
|
|
n |
|
|
||||
б) |
− 1 |
, 2 |
,− |
3 |
, |
|
|
4 |
.... |
Отв. an = (−1)n |
|
|
. |
|||||||||
|
13 |
|
3n +1 |
|||||||||||||||||||
|
4 |
7 |
10 |
|
|
|
|
|
|
|
||||||||||||
2.Пользуясь |
|
|
|
|
определением |
1, докажите, что число A является пределом |
||||||||||||||||
числовой последовательности с заданным общим элементом. Найдите номерN , |
||||||||||||||||||||||
если ε = 0,01. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
а) |
an |
= |
|
|
|
n +1 |
|
, |
A =1. |
Отв. |
N =197 . |
|||||||||||
|
n +3 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
б) |
an |
= |
|
|
|
1 |
, |
|
|
|
|
|
A = 0 . |
Отв. |
N =100 . |
|||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3. Банк выплачивает проценты ежемесячно. Какой должна быть номинальная процентная ставка, чтобы первоначальный вклад увеличился к концу года в С раз?
Отв. P≈100 lnC (приближенно);
P =1200(12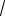 C −1) (точно).
C −1) (точно).
ЧАСТЬ 2.ПРЕДЕЛ ФУНКЦИИ.
2.1 Окрестность точки.
Определение 2. Окрестностью точки а радиуса (или δ-окрестностью точки
Рассмотрим на числовой оси ОХ точку с координатой х=а.
а) называетсяδ множество точек оси ОХ, расстояние от которых до данной точки меньше . δ-
Высказывание: «Точка х лежит в окрестности точки а» можно записать с помощью математической символики следующими четырьмя равносильными
1)x −a <δ
2)x Uδ(a)
3)x (a −δ, a +δ),
4)a −δ < x < a +δ ,способами.
Если точка а исключается из своей |
Рис.4 |
||||||||||
|
|||||||||||
окрестности, то окрестность называется |
|
||||||||||
проколотой. Точка х лежит в |
|
||||||||||
проколотой |
|
окрестности точки а тогда |
|
||||||||
и только |
тогда, |
когда 0 < |
|
x −a |
|
<δ |
. С |
|
|||
|
|
|
|||||||||
|
δ- |
|
|
|
|
|
|
|
|
||
помощью значков теории множеств это |
Рис.5 |
||||||||||
обозначается как x Ůδ(a). |
|
|
|||||||||
Рассмотрим |
теперь «точку, бесконечно удаленную от начала координат». |
||||||||||
|
|
|
|
||||||||
7
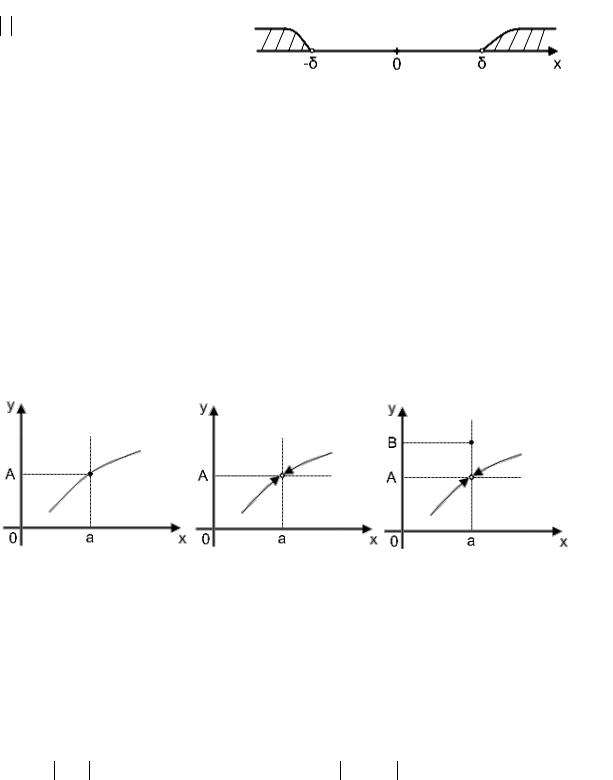
Определение 3.Окрестностью радиуса δ бесконечно удаленной точки x = ∞, принадлежащей оси ОХ, называется множество точек этой оси, расстояние от которых до началаδ координат больше δ .
Проколотая -окрестность для бесконечно удаленной точки совпадает с непроколотой. Попадание точки х в эту окрестность можно задать одним из
1)x > δ ,∞
2)x Uδ( ),
3)x (−∞,−δ) (δ,+∞),следующих способов.
4) x > δ |
, |
Рис.6 |
x < −δ |
|
|
Как видим из рис.6, бесконечно удаленная точка содержит два варианта, при которых точка x может оказаться в ее окрестности. Это возможно при и при x → +∞.
Аналогичным образом можно рассматривать окрестности точек (в том числе,
бесконечно удаленной точки) на оси ОУ. |
|
|
|
2.2 Предел функции при xa. |
|
|
|
Рассмотрим несколько случаев поведения функции |
в окрестности точки x = a . |
||
1) |
функция определена в точке x = a и |
f (a)= A (рис.7), |
|
2) |
функция не определена в точке x = a |
(рис.8), |
|
3) |
функция определена в точке x = a и |
f (a)= B ≠ A |
(рис.9). |
Рис.7 |
Рис.8 |
Рис.9 |
Во всех рассмотренных случаях |
x → a , а функция |
f (x)→ A, что можно |
записать как lim f (x)= A .
x→a
Поведение всех графиков таково, что чем меньше х отличается от а, тем значение функции ближе к числу А. Однако, поведение функции при х=а не является существенным. Этот факт можно сформулировать следующим образом.
Определение 4.Число A называется пределом функции y = f (x) при x → a ,
если для любого ε > 0 найдется δ > 0 , такое что для всех x , удовлетворяющих условию 0 < x −a <δ , выполняется неравенство f (x)− A < ε .
Другими словами, если аргумент х принадлежит проколотой  -окрестности точки а на оси ОХ, то значение функции f(x) принадлежит
-окрестности точки а на оси ОХ, то значение функции f(x) принадлежит  -окрестности точки A на оси ОУ.
-окрестности точки A на оси ОУ.
8
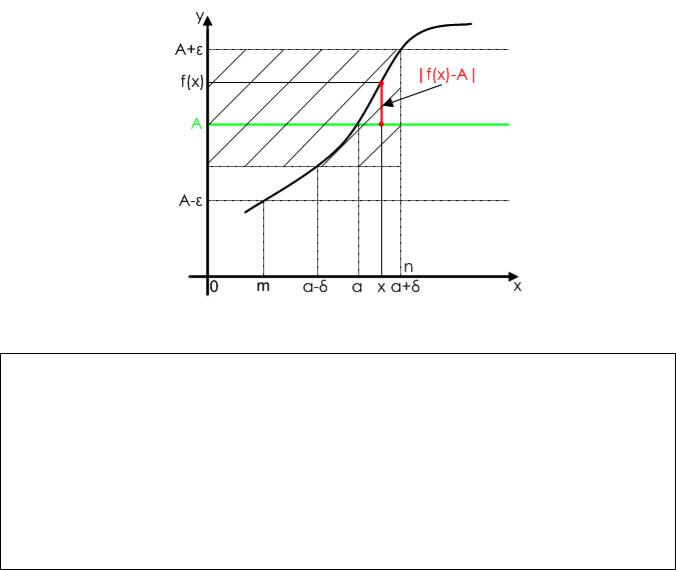
Геометрическая иллюстрация определения 4 представлена на рис.10.
Рис.10
Пояснения к рис.10
На оси ОУ строим окрестность точки y = A произвольного радиуса ε . Прямые
y = A −ε и y = A +ε |
пересекают график функции |
y = f (x) в точках с абсциссами |
|||||||
x = m и x = n . Выберем наименьшее из чисел (a −m) |
и (n −a), обозначим его как |
||||||||
δ . Очевидно, что δ |
зависит от ε ; если уменьшить |
то уменьшится и |
. Выбор |
||||||
δ(ε) |
фиксирует на оси ОХ |
δ |
-окрестность точки x |
= |
aε,. И если |
x→a |
δ, то взяв |
||
|
|
|
|
|
lim f (x)= A |
||||
любой x (a −δ, a) (a, a +δ), получим значение функции y = f (x), которому будет
соответствовать точка на оси ОУ, обязательно принадлежащая ε -окрестности точки A .
Отметим, что описанный выше способ выбора δ(ε) не является единственно возможным: всегда можно изменить δ(ε) в меньшую сторону. Такой подбор δ «с запасом» иногда позволяет обойти трудности, связанные с точным решением
неравенства |
|
f (x)− A |
|
< ε относительно х. |
|
|
|||||
|
|
|
|
||||||||
• |
|
|
|
|
|
ε>0 |
δ>0: x Ů (a)δ f(x) U (Aε). |
||||
A = lim f (x)= |
|||||||||||
Определение 4 можно записать в символах одним из следующих способов. |
|||||||||||
• |
|
|
|
def |
ε |
>0 |
δ |
δ |
|
ε |
|
|
|
x→a |
|||||||||
A = lim f (x)= |
|
|
>0: 0<|x-a|< |
|
|f(x)-A|< . |
||||||
|
|
|
x→a |
|
|
|
|
|
|
||
def
Замечание 1. Все определения предела функции (как уже сформулированное определение 4, так и последующие) состоят из двух частей: внутренней и внешней. Внутренняя часть (синий цвет) описывает поведение аргумента функции, внешняя часть (красный цвет) – поведение значений функции.
9
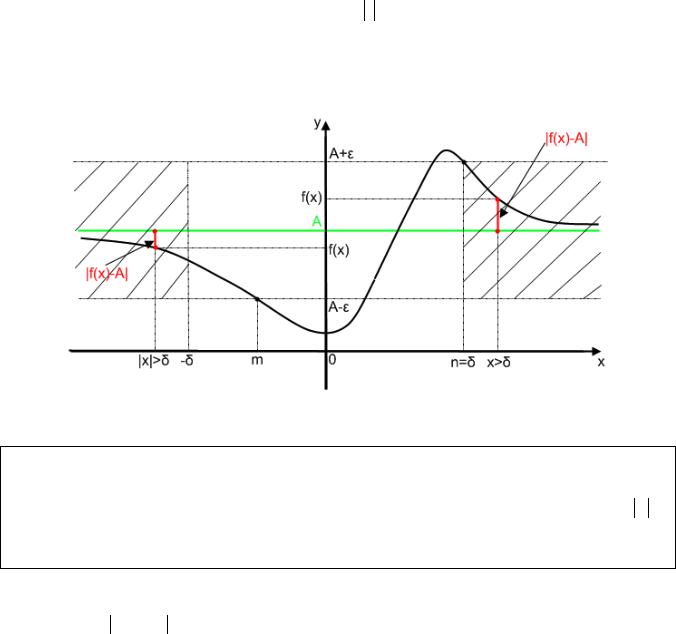
2.3 Предел функции при x∞.
Если существует число A , которое является пределом функции y = f (x) при x → ∞, то это означает, что чем больше x , тем значения функции меньше
отличаются от этого числа A .
Рассмотрим графическую иллюстрацию такого поведения функции, а затем сформулируем его определение.
Рис.11
Так же как в предыдущем случае построим ε -окрестности точки A на оси ОУ, выбрав ε произвольно. Прямые y = A −ε и y = A +ε пересекают график функции
y = f (x) в точках с абсциссами x = m и x = n . Выбрав наибольшее из чисел m и
n , обозначим его как δ , которое, конечно, зависит от заданного ε . На рис.11 δ(ε)= n .
Таким образом, задав ε , мы нашли соответствующую ему δ -окрестность бесконечно удаленной точки. И теперь, чем значение х ближе к бесконечности, тем меньше f (x)− A (т.е. различие между f(x) и числом A ).
Здесь, как и в предыдущем случае, возможен подборδ «с запасом»; однако, изменения δ допустимы не в меньшую, а в большую сторону.
Определение 5. Число |
A называется пределом функции y = f (x) при x → ∞, |
|||||||||||||||||||
т.е. lim f (x)= A, если для любого |
ε > 0 |
найдется δ > 0 , |
такое что для всех x , |
|||||||||||||||||
x→∞ |
|
|
|
|
|
|
|
|
> δ , выполняется неравенство |
|
f (x)− A |
|
< ε . |
|||||||
удовлетворяющих условию |
|
x |
|
|
|
|||||||||||||||
|
|
|
|
|||||||||||||||||
|
|
|
ε>0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Или в символах: |
δ>0: x |
>δ |
|
ε |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
• |
|
def |
|
>0 |
|
|
|
|
>0: |x| |
|
|
|f(x)-A|< . |
|
|
|
|
|
|
||
A = lim f (x)= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
x→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
• |
|
def |
|
|
|
|
|
|
|
|
Ů ( |
|
) |
f(x) U (A). |
|
|
|
|
|
|
A = lim f (x)= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
x→∞ |
|
ε |
|
δ |
|
δ |
∞ |
|
ε |
1 |
|
|
|
|
|||||
Пример 5. |
|
|
|
|
= 0 . |
|
|
|||||||||||||
|
|
Докажем, пользуясь определением, что lim |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→∞ x |
|
|
|
|
|
10
