
Методичка_Пределы_2_Предел_послед_и_Опр_пред_функц
.pdf
Решение. По определению 5 lim 1 |
= 0 , если для любого ε > 0 найдется δ(ε)> 0 , |
||||||||||||
|
|
|
|
|
|
|
|
x→∞ x |
|
|
|
|
|
такое что |
для всех x , |
удовлетворяющих условию |
|
x |
|
>δ(ε) , выполняется |
|||||||
|
|
||||||||||||
неравенство |
|
f (x)−0 |
|
< 0 , т.е. |
|
1 |
|
< ε . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Последнее неравенство равносильно неравенству x > ε1 . Теперь очевидно, что
требуемое по определению 5 неравенство будет выполняться, если δ(ε)= ε1 . То
есть соответствующее δ(ε) нашлось.
Так например, если ε1 = 0,1, то δ =10 и при x >10 выполняется неравенство
f (x) < ε1 . |
f (x) < ε2 . |
А если ε2 = 0,01, то δ =100 и только при x >100 |
И какое бы малое ε мы ни выбрали, найдется δ(ε) такое, что для всех x , удовлетворяющих условию x > δ , соответствующие им значения функции y = f (x) будут отличаться от A = 0 меньше, чем на ε , что и требовалось доказать.
Функции, имеющие предел 0, – важнейший частный случай функций, имеющих конечный предел. Такие функции называются бесконечно малыми.
Теорема (о связи функции, ее предела и бесконечно малой). Функция f(x) имеет при данном стремлении аргумента конечный предел А тогда и только тогда, когда она представима в виде суммы f(x)= А+ (x), где (x) – бесконечно малая (при том же самом стремлении аргумента).
2.4 Бесконечный предел функции. |
|
|
|
|
|
|
|
|
|
Примером функции, |
имеющей бесконечный |
предел |
в точке x = a |
, может |
|||||
служить дробно-рациональная функция |
f (x)= |
P (x) |
|
которой Qn (a)= 0 и |
|||||
m |
, |
у |
|||||||
Qn (x) |
|||||||||
P (a)≠ 0 Простейший пример: f(x)=1/х |
при |
|
|
|
|
|
|
||
примереm .5!) |
|
|
x |
0 |
(но не |
x |
∞, как это было в |
||
Запись lim f (x)= ∞ |
означает в |
этом |
случае, что |
чем ближе |
значение |
||||
x→a |
|
|
|
|
|
|
|
|
|
аргумента х к а, тем функция все более возрастает (по модулю) и, какое бы большое число мы ни задали, в процессе изменения f (x) его превзойдет.
Рассмотрим графическую иллюстрацию такого поведения функции, а затем сформулируем его определение.
Так как y = f (x) при x → a стремится к бесконечности, зададим сколь угодно большое ε > 0 и отметим его на оси ОУ, построив тем самым ε -окрестность бесконечно удаленной точки на оси ОУ.
11
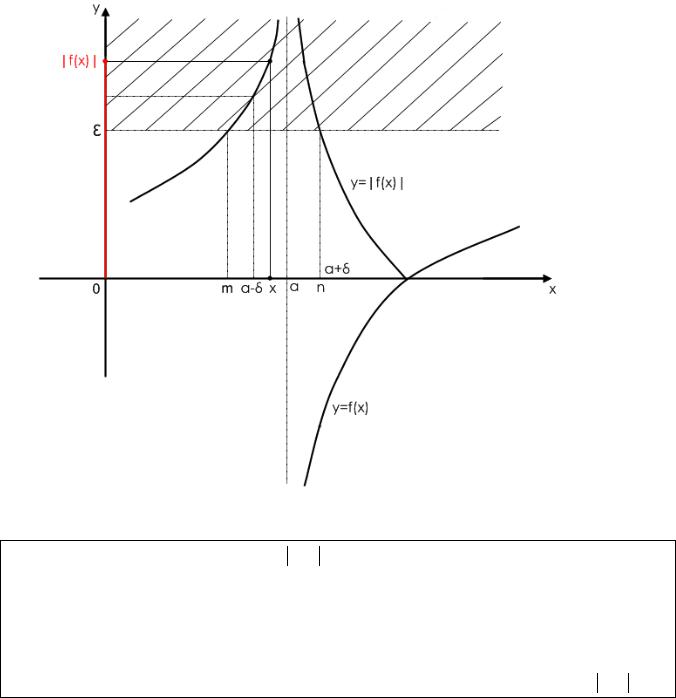
Рис.12
Построим график функции y = f (x) и найдем точки его пересечения с прямой y = ε . На оси ОХ им соответствуют точки x = m, x = n .Выбирая наименьшее из
чисел (a −m) и (n −a), обозначим его как δ .Очевидно, что δ |
зависит от ε . Выбор |
δ(ε)фиксирует на оси ОХ δ -окрестность точки x = a . И если |
lim f (x)= ∞ ( о знаке |
|
x→a |
бесконечности пока не говорим), то любому значению х из проколотой δ - окрестности точки а будет соответствовать значение функции такое, что f (x) > ε .
Если lim f (x)= ∞, то говорят, что функция является бесконечно большой при
x→a
x → a . (Т.е., бесконечно большая функция – то же самое, что и функция, имеющая бесконечный предел.)
Определение 6. |
Функция |
y = f (x) |
|
является |
бесконечно |
|
большой при |
||||||||||
x → a (lim f (x)= ∞ ), если для любого ε > 0 |
найдется δ > 0 , такое что для всех x , |
||||||||||||||||
x→a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) |
|
|
удовлетворяющих условию 0 < |
|
x −a |
|
<δ , выполняется неравенство |
|
|
> ε . |
||||||||||
|
|
|
|||||||||||||||
|
|
||||||||||||||||
В символах это определение можно записать следующим образом. |
|||||||||||||||||
• |
|
def |
>0 |
>0: 0<|x-a|< |
|
|f(x)|> |
|
|
|
|
|
||||||
lim f (x)= ∞ = |
|
|
|
|
|
|
|||||||||||
|
→a |
|
ε>0 |
δ>0: x |
Ů (a)δ f(x) |
U ε( |
. ). |
|
|
|
|
||||||
• |
limx |
f (x)= ∞ = |
12 |
||||||||||||||
|
x→a |
def |
ε δ |
|
δ |
|
ε |
∞ |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Учитывая опыт рассмотренных случаев различного поведения функции, сформулируем теперь определение бесконечного предела функции при x → ∞. .
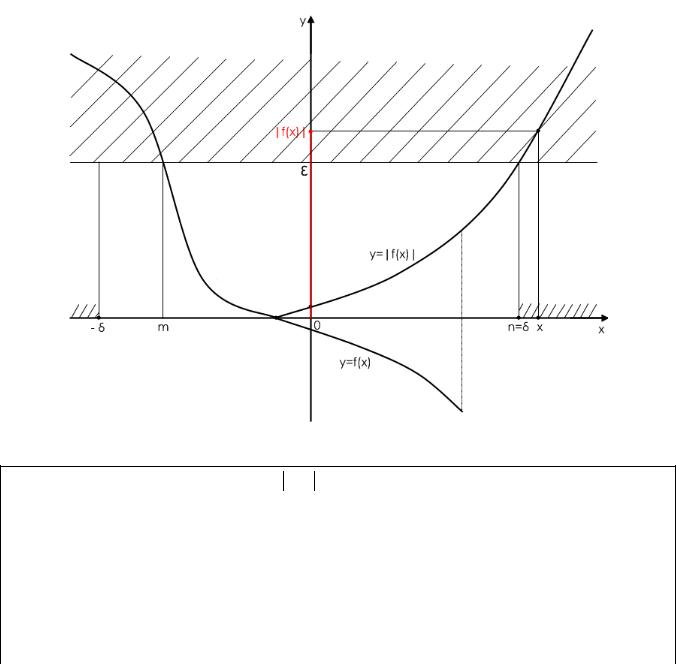
Рассмотрим графическую иллюстрацию такого поведения функции.
Рис.13
Построим график функции y = f (x) и, так как f (x)→ ∞, выберем сколь угодно большое число ε 0 , задав таким образом ε -окрестность бесконечно удаленной
точки на оси ОУ. |
Прямая y = ε пересекает график |
|
функции в точках с |
||
абсциссами x = m |
и x = n . Выбрав наибольшее из чисел |
|
m |
|
и n , обозначим его |
|
|
||||
как δ , которое, конечно, зависит от заданного ε . Таким образом, задав ε , мы
нашли соответствующую ему δ -окрестность бесконечно удаленной точки |
|
. И |
|||||||||||||||||||
если lim f (x)= ∞ |
, то для любой точки x |
|
Ů ( ), |
значение функции y = |
|
f (x) |
|
|
|||||||||||||
|
|
|
|||||||||||||||||||
→∞ |
|
|
|
|
|
|
|
|
|
|
|
δ ∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
окажетсяx |
больше выбранного ε . |
|
|
|
|
|
|
|
|
|
|
||||||||||
Определение |
7. Функция |
y = f (x) |
|
является |
бесконечно большой |
|
при |
||||||||||||||
x → ∞( lim f (x)= ∞ ), если для любого ε > 0 |
найдется δ > 0, |
такое что для всех x , |
|||||||||||||||||||
x→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) |
|
|
|
|
|
|
|
удовлетворяющих условию |
|
x |
|
> δ , выполняется неравенство |
|
|
> ε . |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
Или в символах. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
• lim |
|
( |
|
def |
ε>0 δ>0: |x|>δ |f(x)|>ε. |
|
|
|
|
|
|
|
|
|
|||||||
|
x |
)= ∞ = |
|
|
|
|
|
|
|
|
|
||||||||||
x→∞ f |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
13
Замечание 2. |
ε |
|
δ |
|
|
∞ |
|
|
∞ |
|
|
• |
def |
>0 |
>0: x Ů ( |
) |
f(x) U ( |
|
). |
||||
lim f (x)= ∞ = |
|
|
|||||||||
|
x→∞ |
|
|
|
|
δ |
|
|
ε |
|
|
|
|
Пользуясь |
условной |
записью, можно дать обобщенное |
|||||||
определение предела функции, которое отражает все рассмотренные случаи
поведения функции в окрестности конечной или бесконечно удаленной точки. |
|||
x→ |
f x |
|
ε>0 δ>0: x Ůδ( ) f(x) Uε( ) |
Обобщенное определение. |
|||
lim |
( |
def |
|
)= = |
|
||
Замечание 3. Существуют функции, вообще не имеющие пределов при данном стремлении – ни конечных, ни бесконечных. Примерами могут служить∞. хорошо известные тригонометрические функции: sinx, cosx, tgx, ctgx – при x
Задачи для самостоятельной работы
В каждом из следующих примеров число 0 или 1 является пределом данной
функции при данном стремлении. Выберите верный вариант и обоснуйте его, |
||||||||
вычисленияа) f (x) =1δ(ε)− x, .)x → 0 |
Отв.:A =1, |
δ = ε . |
|
|
||||
пользуясь соответствующим определением предела. (Т.е. укажите формулу для |
||||||||
б) |
f (x) = 1 , x →1 |
Отв.:A =1, |
δ = |
ε |
. |
|||
1+ε |
||||||||
|
x |
|
|
|
|
|||
в) |
f (x) = sin x , |
x → ∞ |
Отв.:A = 0, |
δ = |
1 |
«с запасом». |
||
|
x |
|
|
|
ε |
|
|
|
|
|
|
|
|
|
π |
||
г) |
f (x) = [cos x], |
x → 0 |
Отв.:A = 0, |
δ |
0; 2 и не зависит от ε |
|||
Напоминание: [z] – целая часть числа z, т.е. наибольшее целое число, не превосходящее z.
14
