
Методичка_Пределы (все части)
.pdf
1. Даны несколько первых элементов числовой последовательности. Составьте выражение общего элемента an .
а)1, 3 , |
5 |
, |
|
7 |
|
...... |
|
|
Отв. an = |
2n −1 |
|
|
|
|||||||||
9 |
16 |
|
|
|
|
|
||||||||||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
n2 |
|
|
n |
|
|
||||
б) |
− 1 |
, 2 |
,− |
3 |
, |
|
|
4 |
.... |
Отв. an = (−1)n |
|
|
. |
|||||||||
|
13 |
|
3n +1 |
|||||||||||||||||||
|
4 |
7 |
10 |
|
|
|
|
|
|
|
||||||||||||
2.Пользуясь |
|
|
|
|
определением |
1, докажите, что число A является пределом |
||||||||||||||||
числовой последовательности с заданным общим элементом. Найдите номерN , |
||||||||||||||||||||||
если ε = 0,01. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
а) |
an |
= |
|
|
|
n +1 |
|
, |
A =1. |
Отв. |
N =197 . |
|||||||||||
|
n +3 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
б) |
an |
= |
|
|
|
1 |
, |
|
|
|
|
|
A = 0 . |
Отв. |
N =100 . |
|||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3. Банк выплачивает проценты ежемесячно. Какой должна быть номинальная процентная ставка, чтобы первоначальный вклад увеличился к концу года в С раз?
Отв. P≈100 lnC (приближенно);
P =1200(12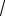 C −1) (точно).
C −1) (точно).
ЧАСТЬ 2.ПРЕДЕЛ ФУНКЦИИ.
2.1 Окрестность точки.
Определение 2. Окрестностью точки а радиуса (или δ-окрестностью точки
Рассмотрим на числовой оси ОХ точку с координатой х=а.
а) называетсяδ множество точек оси ОХ, расстояние от которых до данной точки меньше . δ-
Высказывание: «Точка х лежит в окрестности точки а» можно записать с помощью математической символики следующими четырьмя равносильными
1)x −a <δ
2)x Uδ(a)
3)x (a −δ, a +δ),
4)a −δ < x < a +δ ,способами.
Если точка а исключается из своей |
Рис.4 |
||||||||
|
|||||||||
окрестности, то окрестность называется |
|
||||||||
проколотой. Точка х лежит в |
|
||||||||
проколотой |
|
окрестности точки а тогда |
|
||||||
|
тогда, когда 0 < x −a <δ |
|
|
||||||
и только |
|
δ- |
|
|
|
|
|
. С |
|
|
|
|
|
|
|
|
|||
помощью значков теории множеств это |
Рис.5 |
||||||||
обозначается как x |
Ůδ(a). |
|
|
||||||
Рассмотрим |
теперь «точку, бесконечно удаленную от начала координат». |
||||||||
|
|
|
|
||||||
7
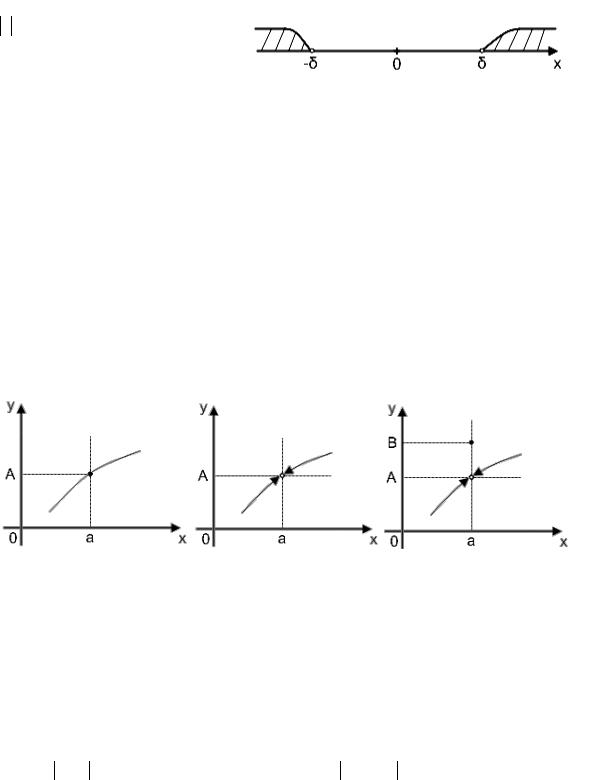
Определение 3.Окрестностью радиуса δ бесконечно удаленной точки x = ∞, принадлежащей оси ОХ, называется множество точек этой оси, расстояние от которых до началаδ координат больше δ .
Проколотая -окрестность для бесконечно удаленной точки совпадает с непроколотой. Попадание точки х в эту окрестность можно задать одним из
1)x > δ ,∞
2)x Uδ( ),
3)x (−∞,−δ) (δ,+∞),следующих способов.
4) x > δ |
, |
Рис.6 |
x < −δ |
|
|
Как видим из рис.6, бесконечно удаленная точка содержит два варианта, при которых точка x может оказаться в ее окрестности. Это возможно при и при x → +∞.
Аналогичным образом можно рассматривать окрестности точек (в том числе,
бесконечно удаленной точки) на оси ОУ. |
|
|
|
2.2 Предел функции при xa. |
|
|
|
Рассмотрим несколько случаев поведения функции |
в окрестности точки x = a . |
||
1) |
функция определена в точке x = a и |
f (a)= A (рис.7), |
|
2) |
функция не определена в точке x = a |
(рис.8), |
|
3) |
функция определена в точке x = a и |
f (a)= B ≠ A |
(рис.9). |
Рис.7 |
Рис.8 |
Рис.9 |
Во всех рассмотренных случаях |
x → a , а функция |
f (x)→ A, что можно |
записать как lim f (x)= A .
x→a
Поведение всех графиков таково, что чем меньше х отличается от а, тем значение функции ближе к числу А. Однако, поведение функции при х=а не является существенным. Этот факт можно сформулировать следующим образом.
Определение 4.Число A называется пределом функции y = f (x) при x → a ,
если для любого ε > 0 найдется δ > 0 , такое что для всех x , удовлетворяющих условию 0 < x −a <δ , выполняется неравенство f (x)− A < ε .
Другими словами, если аргумент х принадлежит проколотой 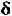 -окрестности точки а на оси ОХ, то значение функции f(x) принадлежит
-окрестности точки а на оси ОХ, то значение функции f(x) принадлежит  -окрестности точки A на оси ОУ.
-окрестности точки A на оси ОУ.
8
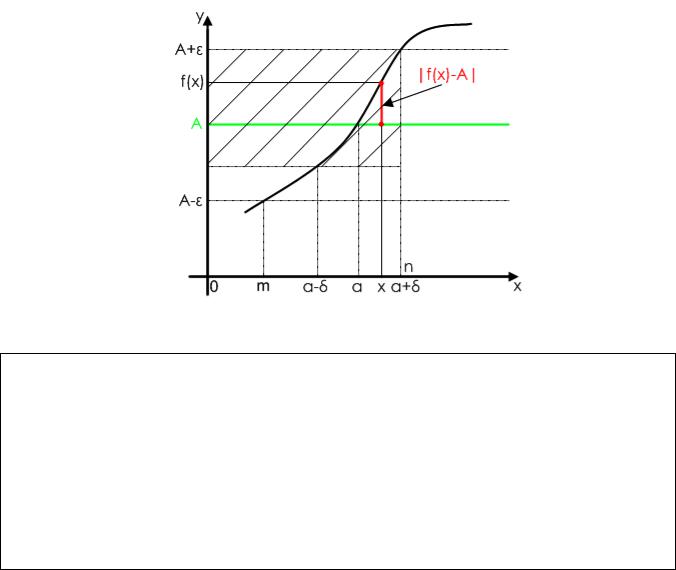
Геометрическая иллюстрация определения 4 представлена на рис.10.
Рис.10
Пояснения к рис.10
На оси ОУ строим окрестность точки y = A произвольного радиуса ε . Прямые
y = A −ε и y = A +ε |
пересекают график функции |
y = f (x) в точках с абсциссами |
|||||||
x = m и x = n . Выберем наименьшее из чисел (a −m) |
и (n −a), обозначим его как |
||||||||
δ . Очевидно, что δ |
зависит от ε ; если уменьшить |
то уменьшится и |
. Выбор |
||||||
δ(ε) |
фиксирует на оси ОХ |
δ |
-окрестность точки x |
= |
aε,. И если |
x→a |
δ, то взяв |
||
|
|
|
|
|
lim f (x)= A |
||||
любой x (a −δ, a) (a, a +δ), получим значение функции y = f (x), которому будет
соответствовать точка на оси ОУ, обязательно принадлежащая ε -окрестности точки A .
Отметим, что описанный выше способ выбора δ(ε) не является единственно возможным: всегда можно изменить δ(ε) в меньшую сторону. Такой подбор δ «с запасом» иногда позволяет обойти трудности, связанные с точным решением
неравенства |
|
f (x)− A |
|
< ε относительно х. |
|
|
|||||
|
|
|
|
||||||||
• |
|
|
|
|
|
ε>0 |
δ>0: x Ů (a)δ f(x) U (Aε). |
||||
A = lim f (x)= |
|||||||||||
Определение 4 можно записать в символах одним из следующих способов. |
|||||||||||
• |
|
|
|
def |
ε |
>0 |
δ |
δ |
|
ε |
|
|
|
x→a |
|||||||||
A = lim f (x)= |
|
|
>0: 0<|x-a|< |
|
|f(x)-A|< . |
||||||
|
|
|
x→a |
|
|
|
|
|
|
||
def
Замечание 1. Все определения предела функции (как уже сформулированное определение 4, так и последующие) состоят из двух частей: внутренней и внешней. Внутренняя часть (синий цвет) описывает поведение аргумента функции, внешняя часть (красный цвет) – поведение значений функции.
9
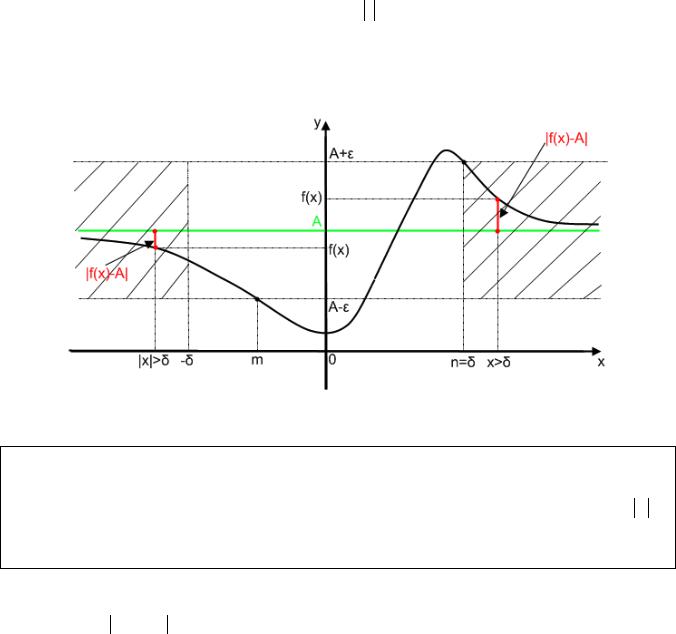
2.3 Предел функции при x∞.
Если существует число A , которое является пределом функции y = f (x) при x → ∞, то это означает, что чем больше x , тем значения функции меньше
отличаются от этого числа A .
Рассмотрим графическую иллюстрацию такого поведения функции, а затем сформулируем его определение.
Рис.11
Так же как в предыдущем случае построим ε -окрестности точки A на оси ОУ, выбрав ε произвольно. Прямые y = A −ε и y = A +ε пересекают график функции
y = f (x) в точках с абсциссами x = m и x = n . Выбрав наибольшее из чисел m и
n , обозначим его как δ , которое, конечно, зависит от заданного ε . На рис.11 δ(ε)= n .
Таким образом, задав ε , мы нашли соответствующую ему δ -окрестность бесконечно удаленной точки. И теперь, чем значение х ближе к бесконечности, тем меньше f (x)− A (т.е. различие между f(x) и числом A ).
Здесь, как и в предыдущем случае, возможен подборδ «с запасом»; однако, изменения δ допустимы не в меньшую, а в большую сторону.
Определение 5. Число |
A называется пределом функции y = f (x) при x → ∞, |
|||||||||||||||||||
т.е. lim f (x)= A, если для любого |
ε > 0 |
найдется δ > 0 , |
такое что для всех x , |
|||||||||||||||||
x→∞ |
|
|
|
|
|
|
|
|
> δ , выполняется неравенство |
|
f (x)− A |
|
< ε . |
|||||||
удовлетворяющих условию |
|
x |
|
|
|
|||||||||||||||
|
|
|
|
|||||||||||||||||
|
|
|
ε>0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Или в символах: |
δ>0: x |
>δ |
|
ε |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
• |
|
def |
|
>0 |
|
|
|
|
>0: |x| |
|
|
|f(x)-A|< . |
|
|
|
|
|
|
||
A = lim f (x)= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
x→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
• |
|
def |
|
|
|
|
|
|
|
|
Ů ( |
|
) |
f(x) U (A). |
|
|
|
|
|
|
A = lim f (x)= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
x→∞ |
|
ε |
|
δ |
|
δ |
∞ |
|
ε |
1 |
|
|
|
|
|||||
Пример 5. |
|
|
|
|
= 0 . |
|
|
|||||||||||||
|
|
Докажем, пользуясь определением, что lim |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→∞ x |
|
|
|
|
|
10

Решение. По определению 5 lim 1 |
= 0 , если для любого ε > 0 найдется δ(ε)> 0 , |
||||||||||||
|
|
|
|
|
|
|
|
x→∞ x |
|
|
|
|
|
такое что |
для всех x , |
удовлетворяющих условию |
|
x |
|
>δ(ε) , выполняется |
|||||||
|
|
||||||||||||
неравенство |
|
f (x)−0 |
|
< 0 , т.е. |
|
1 |
|
< ε . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Последнее неравенство равносильно неравенству x > ε1 . Теперь очевидно, что
требуемое по определению 5 неравенство будет выполняться, если δ(ε)= ε1 . То
есть соответствующее δ(ε) нашлось.
Так например, если ε1 = 0,1, то δ =10 и при x >10 выполняется неравенство
f (x) < ε1 . |
f (x) < ε2 . |
А если ε2 = 0,01, то δ =100 и только при x >100 |
И какое бы малое ε мы ни выбрали, найдется δ(ε) такое, что для всех x , удовлетворяющих условию x > δ , соответствующие им значения функции y = f (x) будут отличаться от A = 0 меньше, чем на ε , что и требовалось доказать.
Функции, имеющие предел 0, – важнейший частный случай функций, имеющих конечный предел. Такие функции называются бесконечно малыми.
Теорема (о связи функции, ее предела и бесконечно малой). Функция f(x) имеет при данном стремлении аргумента конечный предел А тогда и только тогда, когда она представима в виде суммы f(x)= А+ (x), где (x) – бесконечно малая (при том же самом стремлении аргумента).
2.4 Бесконечный предел функции. |
|
|
|
|
|
|
|
|
|
Примером функции, |
имеющей бесконечный |
предел |
в точке x = a |
, может |
|||||
служить дробно-рациональная функция |
f (x)= |
P (x) |
|
которой Qn (a)= 0 и |
|||||
m |
, |
у |
|||||||
Qn (x) |
|||||||||
P (a)≠ 0 Простейший пример: f(x)=1/х |
при |
|
|
|
|
|
|
||
примереm .5!) |
|
|
x |
0 |
(но не |
x |
∞, как это было в |
||
Запись lim f (x)= ∞ |
означает в |
этом |
случае, что |
чем ближе |
значение |
||||
x→a |
|
|
|
|
|
|
|
|
|
аргумента х к а, тем функция все более возрастает (по модулю) и, какое бы большое число мы ни задали, в процессе изменения f (x) его превзойдет.
Рассмотрим графическую иллюстрацию такого поведения функции, а затем сформулируем его определение.
Так как y = f (x) при x → a стремится к бесконечности, зададим сколь угодно большое ε > 0 и отметим его на оси ОУ, построив тем самым ε -окрестность бесконечно удаленной точки на оси ОУ.
11
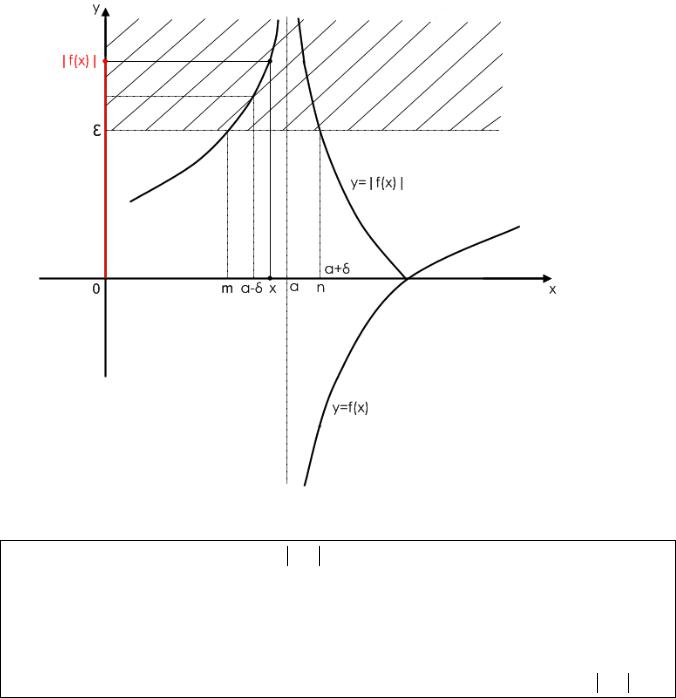
Рис.12
Построим график функции y = f (x) и найдем точки его пересечения с прямой y = ε . На оси ОХ им соответствуют точки x = m, x = n .Выбирая наименьшее из
чисел (a −m) и (n −a), обозначим его как δ .Очевидно, что δ |
зависит от ε . Выбор |
δ(ε)фиксирует на оси ОХ δ -окрестность точки x = a . И если |
lim f (x)= ∞ ( о знаке |
|
x→a |
бесконечности пока не говорим), то любому значению х из проколотой δ - окрестности точки а будет соответствовать значение функции такое, что f (x) > ε .
Если lim f (x)= ∞, то говорят, что функция является бесконечно большой при
x→a
x → a . (Т.е., бесконечно большая функция – то же самое, что и функция, имеющая бесконечный предел.)
Определение 6. |
Функция |
y = f (x) |
|
является |
бесконечно |
|
большой при |
||||||||||
x → a (lim f (x)= ∞ ), если для любого ε > 0 |
найдется δ > 0 , такое что для всех x , |
||||||||||||||||
x→a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) |
|
|
удовлетворяющих условию 0 < |
|
x −a |
|
<δ , выполняется неравенство |
|
|
> ε . |
||||||||||
|
|
|
|||||||||||||||
|
|
||||||||||||||||
В символах это определение можно записать следующим образом. |
|||||||||||||||||
• |
|
def |
>0 |
>0: 0<|x-a|< |
|
|f(x)|> |
|
|
|
|
|
||||||
lim f (x)= ∞ = |
|
|
|
|
|
|
|||||||||||
|
→a |
|
ε>0 |
δ>0: x |
Ů (a)δ f(x) |
U ε( |
. ). |
|
|
|
|
||||||
• |
limx |
f (x)= ∞ = |
12 |
||||||||||||||
|
x→a |
def |
ε δ |
|
δ |
|
ε |
∞ |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
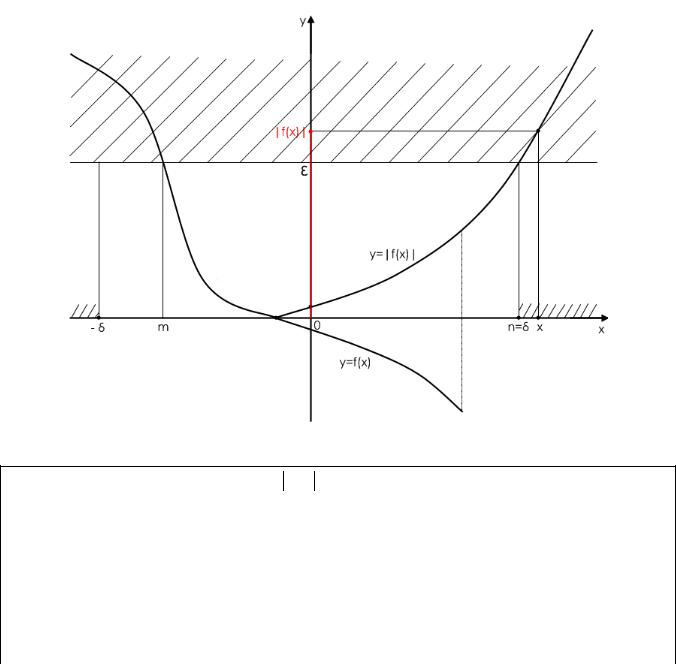
Учитывая опыт рассмотренных случаев различного поведения функции, сформулируем теперь определение бесконечного предела функции при x → ∞. .
Рассмотрим графическую иллюстрацию такого поведения функции.
Рис.13
Построим график функции y = f (x) и, так как f (x)→ ∞, выберем сколь угодно большое число ε 0 , задав таким образом ε -окрестность бесконечно удаленной
точки на оси ОУ. |
Прямая y = ε пересекает график |
|
функции в точках с |
||
абсциссами x = m |
и x = n . Выбрав наибольшее из чисел |
|
m |
|
и n , обозначим его |
|
|
||||
как δ , которое, конечно, зависит от заданного ε . Таким образом, задав ε , мы
нашли соответствующую ему δ -окрестность бесконечно удаленной точки |
|
. И |
|||||||||||||||||||
если lim f (x)= ∞ |
, то для любой точки x |
|
Ů ( ), |
значение функции y = |
|
f (x) |
|
|
|||||||||||||
|
|
|
|||||||||||||||||||
→∞ |
|
|
|
|
|
|
|
|
|
|
|
δ ∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
окажетсяx |
больше выбранного ε . |
|
|
|
|
|
|
|
|
|
|
||||||||||
Определение |
7. Функция |
y = f (x) |
|
является |
бесконечно большой |
|
при |
||||||||||||||
x → ∞( lim f (x)= ∞ ), если для любого ε > 0 |
найдется δ > 0, |
такое что для всех x , |
|||||||||||||||||||
x→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) |
|
|
|
|
|
|
|
удовлетворяющих условию |
|
x |
|
> δ , выполняется неравенство |
|
|
> ε . |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
Или в символах. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
• lim |
|
( |
|
def |
ε>0 δ>0: |x|>δ |f(x)|>ε. |
|
|
|
|
|
|
|
|
|
|||||||
|
x |
)= ∞ = |
|
|
|
|
|
|
|
|
|
||||||||||
x→∞ f |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
13
Замечание 2. |
ε |
|
δ |
|
|
∞ |
|
|
∞ |
|
|
• |
def |
>0 |
>0: x Ů ( |
) |
f(x) U ( |
|
). |
||||
lim f (x)= ∞ = |
|
|
|||||||||
|
x→∞ |
|
|
|
|
δ |
|
|
ε |
|
|
|
|
Пользуясь |
условной |
записью, можно дать обобщенное |
|||||||
определение предела функции, которое отражает все рассмотренные случаи
поведения функции в окрестности конечной или бесконечно удаленной точки. |
|||
x→ |
f x |
|
ε>0 δ>0: x Ůδ( ) f(x) Uε( ) |
Обобщенное определение. |
|||
lim |
( |
def |
|
)= = |
|
||
Замечание 3. Существуют функции, вообще не имеющие пределов при данном стремлении – ни конечных, ни бесконечных. Примерами могут служить∞. хорошо известные тригонометрические функции: sinx, cosx, tgx, ctgx – при x
Задачи для самостоятельной работы
В каждом из следующих примеров число 0 или 1 является пределом данной
функции при данном стремлении. Выберите верный вариант и обоснуйте его, |
||||||||
вычисленияа) f (x) =1δ(ε)− x, .)x → 0 |
Отв.:A =1, |
δ = ε . |
|
|
||||
пользуясь соответствующим определением предела. (Т.е. укажите формулу для |
||||||||
б) |
f (x) = 1 , x →1 |
Отв.:A =1, |
δ = |
ε |
. |
|||
1+ε |
||||||||
|
x |
|
|
|
|
|||
в) |
f (x) = sin x , |
x → ∞ |
Отв.:A = 0, |
δ = |
1 |
«с запасом». |
||
|
x |
|
|
|
ε |
|
|
|
|
|
|
|
|
|
π |
||
г) |
f (x) = [cos x], |
x → 0 |
Отв.:A = 0, |
δ |
0; 2 и не зависит от ε |
|||
Напоминание: [z] – целая часть числа z, т.е. наибольшее целое число, не превосходящее z.
14
3. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ
3.1. Некоторые теоремы о пределах и непрерывности.
Все теоремы данного подпункта сформулированы для пределов∞ функций. Однако, теоремы 1, 2 и 4 верны и для последовательностей при n .
Мы ограничимся теоремами, которые позволят нам начать знакомство с техникой вычисления пределов. Разумеется, они не охватывают всего круга теорем о пределах и непрерывности, входящих в курс математического анализа.
Теорема 1. Если при x → функция F(x) - бесконечно большая, то функция
1 |
|
- бесконечно малая (и наоборот). |
|
||||
F(x) |
|
||||||
|
|
|
|
|
|
||
|
Теорема 2. Если существуют конечные пределы lim f (x)= A |
и lim g(x)= B , то |
|||||
|
|
|
|
|
|
x→ |
x→ |
|
|
lim(f (x)± g(x))= A ± B, |
|
||||
|
|
x→ |
|
|
|
|
|
|
|
lim(f (x) g(x))= AB, |
|
||||
|
|
limx→ |
f (x) |
= |
A |
, B ≠ 0. |
|
|
|
|
|
|
|||
|
|
x→ g(x) |
B |
|
|||
Определение (VIP). Функция непрерывна в точке x = a , если lim f (x)= f (a).
x→a
Теорема 3. Любая элементарная функция непрерывна в каждой внутренней
точке своей области определения. |
|
Теорема 4. Пусть limϕ(x)= a и функция |
f (z) непрерывна в точке a . Тогда |
x→ |
|
lim f (ϕ(x)) = f (a) . |
|
x→ |
|
3.2 Некоторые формулы и приемы элементарной математики, используемые при вычислении пределов.
Формулы сокращенного умножения
А1) a2 −b2 = (a −b)(a +b) ; А2) a3 −b3 = (a −b)(a2 + ab +b2 ) ; А3) a3 +b3 = (a +b)(a2 − ab +b2 ) .
Формулы, содержащие корни
К1) q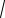 a p = a p / q ( a > 0, p Z, q N, p / q − несократимая дробь);
a p = a p / q ( a > 0, p Z, q N, p / q − несократимая дробь);
К2) x2 = x = x, x ≥ 0 .
− x, x < 0
Другие формулы с корнями сводятся к показательным формулам в силу К1).
Логарифмические≠ формулы. Во всех формулах этого раздела a>0, a 1, b>0.
Л1) aloga b=b. В частности, eln b = b .
1
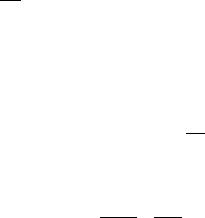
Л2) c > 0, c ≠1 loga b = logc b |
. В частности, |
loga b = ln b . |
logc a |
|
ln a |
Остальные логарифмические формулы приведем только для натуральных логарифмов, поскольку все вычисления можно (и рекомендуется) сводить к ним.
Л3) ln1 = 0 .
Л4) ln a −ln b = ln ba .
Л5) k R ln(bk ) = k ln b . В частности, ln b1 = −ln b .
Показательные формулы. Во всех формулах этого раздела a>0.
П1) a−p = a1p .
П2) a p+q = a p aq .
П3) a p−q = a p .
aq
П4) a pq = (a p )q = (aq ) p .
П5) При b > 0 (ab) p = a pb p , (ba) p = ba pp .
П6) a0 =1.
Тригонометрические формулы. В формулах этого раздела k Z .
Т1) tg α = cossinαα , ctgα = cossinαα = tg1α .
Т2) sinπk = tgπk = 0, cosπk = (−1)k . Используя обозначения, принятые при
вычислении пределов, можно также записывать условную формулу ctgπk = ∞ (см. теорему 1).
Т3) Формулы четности и периодичности
sin(- |
sin |
|
|
|
|
|
|
sin(α + 2πk) = sinα ; |
|
|
|
|
|
|
|
|
|
cos(- |
cos |
|
|
|
|
|
|
cos(α + 2πk) = cosα ; |
|
|
|
|
|
|
|
|
|
tg(-α)=-tgα |
|
|
|
|
|
|
tg(α +πk) = tgα ; |
|
|
|
|
|
|
|
|
||
ctg(-α)=-ctgα |
|
|
|
|
ctg(α +πk) = ctgα . |
|||
|
|
|
|
|
|
|
|
|
Т4) sin2 α + cos2 α =1. |
α − β cos |
α + β ; |
||||||
Т5) а) sinα −sin β = 2sin |
||||||||
|
|
2 |
|
|
2 |
|
|
|
б) cosα −cos β = 2sin |
|
β −α |
sin |
β +α |
; |
|||
2 |
|
|
||||||
|
|
|
|
2 |
|
|
||
в) tgα − tg β = |
sin(α − β) |
; |
|
|
|
|
||
|
cosα cos β |
|
|
|
|
|
||
г) ctgα −ctg β = sin(β −α) . sinα sin β
2
