
МАОС без 1 главы
.pdf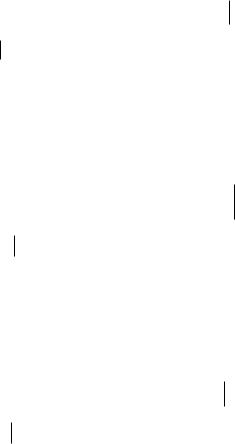
2. Сигнал на входе устройства отсутствует (состояние A0), и устройство
обнаружения принимает решение |
* |
об отсутствии сигнала. Такая ситуация |
A0 |
называется правильным необнаружением, и безусловная вероятность существования такой ситуации
|
|
|
* |
* |
A 0) P( A 0)P ˆ , |
|
|
|
P( A 0 A 0) P( A 0)P( A 0 |
||
|
|
|
|
|
F |
где |
P ˆ |
* |
A 0) – условная вероятность правильного необнаружения. |
||
P( A 0 |
|||||
|
F |
|
|
|
|
|
3. |
Сигнал на входе устройства отсутствует (состояние A0 ), но устрой- |
|||
ство обнаружения принимает решение |
* |
о наличии сигнала (ошибка перво- |
|||
A1 |
|||||
го рода). Такая ситуация называется ложной тревогой, и безусловная вероятность существования такой ситуации
|
P( A* A |
0 |
) P( A |
0 |
)P( A* A |
0 |
) P( A |
0 |
)P , |
(2.6) |
|
|
1 |
|
|
1 |
|
F |
|
||||
* |
A 0) – условная вероятность ложной тревоги. |
|
|||||||||
где PF P( A 1 |
|
||||||||||
4. Сигнал на входе устройства присутствует (состояние A1), но устрой- |
|||||||||||
ство обнаружения принимает решение |
* |
об отсутствии сигнала (ошибка |
|||||||||
А0 |
|||||||||||
второго рода). Такая ситуация называется пропуском цели, и безусловная вероятность существования такой ситуации
|
|
|
* |
* |
A1) P( A1)P |
ˆ , |
(2.7) |
|
|
|
P( A 0 A1) P( A1)P( A 0 |
||||
|
|
|
|
|
D |
|
|
где |
P ˆ |
* |
A1) – условная вероятность пропуска цели. |
|
|||
P( A 0 |
|
||||||
|
D |
|
|
|
|
|
|
|
Нетрудно убедиться, что |
PD P ˆ 1, |
PF P ˆ 1, |
т. е. из четырех услов- |
|||
|
|
|
|
D |
F |
|
|
ных вероятностей независимыми являются только две. Из предыдущего ясно
также, что соотношением между P |
и |
P |
, P |
и |
P |
можно управлять, изме- |
D |
|
D |
F |
|
F |
|
няя порог l0 в выражении (3.5). Таким образом, встает задача об оптимальном выборе значения порога отношения правдоподобия l0.
2.4. Критерии оптимального обнаружения
В зависимости от имеющейся априорной информации о свойствах сигнала и помехи и от опасности ошибок первого и второго родов предложены различные критерии для выбора порога l0. Если известна априорная вероятность появления сигнала и ошибкам первого и второго родов можно припи-
33

сать определенные стоимости или штрафы, то можно говорить о некотором среднем риске r принятия неправильного решения:
r r |
P( A |
* |
A |
|
) r |
ˆ |
P( A |
|
A ) , |
|
1 |
0 |
0 |
||||||||
F |
|
|
|
|
1 |
|||||
|
|
|
|
|
D |
|
|
|
||
где rF – стоимость риска ложной тревоги;
r ˆ D
– стоимость риска пропуска
цели. Если учесть равенства (2.6) и (2.7), а также то, что P(A0)=1 P(A1) , выражение для среднего риска можно записать в виде
|
|
|
r r |
1 P(A ) P |
r |
ˆ |
P(A )P |
ˆ |
min . |
||
|
|
|
F |
1 |
F |
|
1 |
|
|
||
|
|
|
|
|
|
D |
|
D |
|
||
Поскольку в соответствии с выражениями (2.2) и (2.3) вероятности оши- |
|||||||||||
бок PF |
и |
P ˆ |
зависят от разбиения области существования переменной (в |
||||||||
|
|
D |
|
|
|
|
|
|
|
|
|
нашем случае – области значений принятого колебания x(t)) на подобласти, т. е. от выбора порога l0 , то, минимизируя средний риск r при изменении l0, можно получить оптимальное значение порога. Этот критерий носит название критерия минимума среднего риска или критерия Байеса. Он применим в
случае, когда можно указать стоимости ошибок rF и r ˆ и известна вероят- D
ность появления сигнала (объекта) Р(A1).
В частном случае, если опасности ложной тревоги и пропуска цели оди-
наковы, т. е. rF rDˆ 1, критерий минимума среднего риска переходит в критерий идеального наблюдателя или критерий Зигерта-Котельникова:
r 1 P( A1 ) PF P( A1 )PD min.
Критерий идеального наблюдателя, как и критерий Байеса, требует знания вероятности появления сигнала (объекта). Однако зачастую при решении задач обнаружения эта вероятность заранее не известна. Часто нельзя указать и стоимости ошибок. В этих случаях применяется критерий НейманаПирсона. Согласно этому критерию, задаются некоторым малым допустимым значением вероятности ложной тревоги PF и требуют максимизации вероятности правильного обнаружения PD. При известной статистике (плотности распределения вероятностей) помехи по заданной условной вероятности PF можно определить пороговое значение l0 и по нему – условную вероятность правильного обнаружения.
2.5. Простейший обнаружитель Неймана-Пирсона
Рассмотрим простейший обнаружитель, работающий в соответствии с критерием Неймана-Пирсона и предназначенный для обнаружения в задан-
34

ный момент времени детерминированного сигнала шума с нулевым средним и известной дисперсией
s на фоне гауссовского
2 . Фиксация момента об- n
наружения приводит к тому, что в выражении (2.4) для отношения правдоподобия n-мерная плотность распределения переходит в одномерную и может быть записана в виде
|
|
|
|
1 |
|
|
|
x |
2 |
|
p |
|
(x) |
|
|
exp |
|
|
. |
||
n |
|
|
|
|
2 |
|||||
|
|
|
2πσn |
|
|
|
|
|||
|
|
|
|
|
|
2σn |
|
|||
Так как при наличии сигнала x(t) = s + n(t), т. е. n(t) = x(t) – s, то плотность распределения смеси сигнала с помехой имеет вид
|
1 |
|
(x s) |
2 |
|
|
|
|
|
|
|
psn (x ) pn (x s) |
2 n |
exp |
2 |
|
. |
|
|
|
|
||
|
2 n |
|
Тогда отношение правдоподобия запишется в виде
l l(x) psn (x) |
pn (x s) |
|
|
|
(x s)2 |
|
|
|||||||
exp |
1 |
|
x2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
p |
n |
(x) |
p |
n |
(x) |
|
2σ |
|
|
|
|||
|
n |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
s |
2 |
|
|
xs |
|
|
|
|
|
|
|
||
exp( |
|
|
|
) exp |
. |
|
|
|
|
|
|
|||
|
|
2 |
2 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
2σn |
|
σn |
|
|
|
|
|
|
|
||||
Первый множитель в этом выражении есть величина постоянная. Тогда отношение правдоподобия есть монотонная функция величины сигнала x, т. е. любому значению x соответствует определенное значение отношения правдоподобия l(x) (рис. 2.2).
Но в этом случае можно перейти от сравнения с порогом l0 отношения правдоподобия l(x) к сравнению с порогом x0 самих значений сигнала x. Тогда условная вероятность ложной тревоги
где
F |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|||
P |
|
p |
|
(x)dx |
|||||
|
|
x |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
2 |
x |
|
t |
2 |
|
|
||
Ф(x ) |
e |
/ 2 |
dt |
||||||
|
|
||||||||
|
|
|
|
|
|||||
|
2 |
|
|
|
|
|
|
||
|
|
0 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
x2 |
|
|
1 |
|
|
x |
|
|
|
||
|
|
|
exp |
|
|
|
|
dx |
|
1 Ф |
|
0 |
|
|
, |
(2.8) |
|
|
|
2 |
|
|
|
|
|
||||||||||
|
2 n x |
|
|
|
|
2 |
|
|
|
|
|
||||||
|
0 |
|
|
|
2 n |
|
|
|
n |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
– интеграл вероятности. При заданной условной
вероятности ложной тревоги из формулы (2.8) может быть определен порог x0 :
x |
0 |
|
Ф 1(1 2 P ), |
(2.9) |
|
n |
F |
|
35

где Ф-1(а) – значение аргумента функции Ф(x) при ее значении, равном а.
l(x) l0
x0 |
x |
Рис. 2.2
Аналогично может быть определена условная вероятность правильного обнаружения:
|
|
|
1 |
|
|
(x s)2 |
1 |
|
s x |
|
|
|
||||||
PD |
|
psn (x)dx |
|
|
exp |
|
|
dx |
|
|
|
|
0 |
|
|
, |
||
|
|
2 |
|
1 Ф |
|
|
|
|||||||||||
|
|
|
|
2πσ |
|
|
|
2σ |
|
2 |
|
|
σn |
|
|
|
||
|
x |
|
|
n x |
|
n |
|
|
|
|
|
|
||||||
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
так как Ф( x) Ф(x) .
Подставляя сюда выражение (2.9), окончательно можно получить
PD |
1 |
|
|
s |
|
1 |
|
2 |
1 |
|
σn |
|
(1 2PF ) . |
||
|
|
|
|
|
|
(2.10)
(2.11)
Таким образом, при заданном значении порога x0 условная вероятность правильного обнаружения зависит как от x0, так и от величины сигнала s. Из выражений (2.10) и (2.11) видно, что при s = 0 PD = PF , при s = x0 PD = 1/2 ,
при s >> x0 PD 1.
На рис. 2.3 приведены так называемые кривые обнаружения, представляющие собой зависимость условной вероятности правильного обнаружения PD от амплитуды сигнала s при заданных условных вероятностях ложной тревоги PF. Видно, что чем меньше заданная условная вероятность ложной тревоги, тем больше сдвигаются кривые обнаружения вправо, т.е для обнаружения сигнала с заданной вероятностью требуются сигналы большей амплитуды. Можно также заметить, что кривые обнаружения начинаются со значений условной вероятности правильного обнаружения, численно равных заданным значениям условной вероятности ложной тревоги. При этом, как
36
видно из рисунка, наклон кривых остается постоянным независимо от условной вероятности ложной тревоги.
PD
1,0
PF2 |
PF1 |
PF1<PF2 |
0,5
|
x02 |
x01 |
s |
|
Рис. 2.3
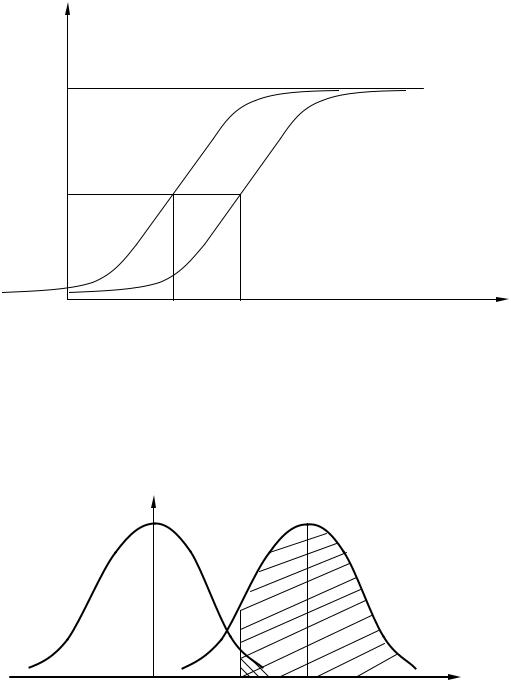
Этот же результат можно пояснить непосредственно по кривым плотностей распределения pn(x) и psn(x), приведенным на рис. 2.4.
p(x)
pn(x) |
psn(x) |
x0 |
S |
Рис. 2.4
x
Участок под кривой pn(x) справа от x0 определяет условную вероятность ложной тревоги, под кривой psn(x) – условную вероятность правильного об-
37

наружения. При смещении кривой psn(x) вправо, что соответствует увеличению сигнала s, вероятность правильного обнаружения возрастает.
Структурная схема простейшего обнаружителя Неймана-Пирсона состоит из одного блока – порогового устройства. На первый вход его подается входной сигнал x(t), на второй вход – пороговое значение x0. Сравнивая значения x(t) c x0, пороговое устройство в каждый момент времени вырабатывает решение о наличии или отсутствии сигнала.
2.6. Бинарное обнаружение полностью известного сигнала
Рассмотренный случай соответствует обнаружению очень короткого сигнала. При обнаружении сигналов конечной длительности, если не требуется очень высокое быстродействие, целесообразно строить обнаружитель так, чтобы использовать полную энергию сигнала. Пусть на вход обнаружителя воздействует смесь сигнала и помехи, описываемая формулой (2.1), где s(t, ) – полностью известный сигнал длительностью T и верхней частотой спектра c , а n(t) – квазибелый гауссовский шум с постоянной спектральной плотностью Sn( )= N0 /2 в полосе частот 
 c . Тогда входное колебание x(t) можно разложить в ряд Котельникова
c . Тогда входное колебание x(t) можно разложить в ряд Котельникова
x(t) |
k |
k |
x |
ψ (t) |
|
|
k |
|
,
xk x(tk ); tk k t; |
N |
T |
; |
k 0;1; 2...N; |
t |
π |
|
1 |
|
; |
|
t |
ω |
|
2 f |
|
|||||||
|
|
|
|
|
|
c |
|||||
|
|
|
|
|
|
c |
|
|
|||
где
ψ |
sin |
c |
(t t |
k |
) |
||
|
|
|
|
|
|||
k |
ω (t t |
|
) |
|
|||
|
k |
|
|||||
|
c |
|
|
|
|
|
|
.
Тогда непрерывная функция x(t) сводится к многомерной случайной величине x = (x1, x2,...), которой можно сопоставить многомерную плотность распределения вероятностей p(x1, x2, ..., xn). Корреляционная функция квазибелого шума может быть записана в виде
|
|
|
sin ω τ |
||
|
|
R(τ) N0 fc |
|
c |
, |
|
|
ω τ |
|||
|
|
|
c |
|
|
дисперсия шума |
2 |
N0 fc . Известно также, |
что сечения квазибелого гаус- |
||
n |
|||||
совского шума, отстоящие на 1/2fc , можно считать независимыми. Тогда многомерная плотность вероятностей может быть определена как произведение независимых плотностей вероятностей сечений xi:
38

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
|
|
p |
|
(x |
, x |
|
|
,...,x |
|
) p(x |
) p(x |
|
)...p(x |
|
) |
|
1 |
|
|
|
exp |
|
|
i 1 |
|
|
|
|
|||||||||||||
n |
2 |
n |
2 |
n |
|
|
|
|
|
n / 2 |
|
|
|
|
|||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
(2πN |
|
f |
|
) |
|
|
2N |
|
f |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
c |
|
|
|
|
0 |
c |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
exp |
|
|
|
|
i 1 |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
n / 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
(2πN |
|
|
f |
|
) |
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
0 |
c |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.12)
Аналогично, плотность распределения вероятностей смеси сигнала с шумом запишется в виде
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
(x |
|
s |
) |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
i |
i |
|
|
|
|
|||||||
|
|
|
psn (x1, x2 ,...,xn ) |
|
|
|
|
|
|
|
|
|
|
exp |
|
|
|
i 1 |
|
|
|
|
|
|
. |
(2.13) |
||||||||||
|
|
|
(2πN |
|
f |
|
) |
n / 2 |
|
|
|
N |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
c |
|
|
|
|
|
0 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где s1 , s2 ,...,si ,...,sn – значения полезного сигнала, взятые в сечениях. |
|
|||||||||||||||||||||||||||||||||||
|
С учетом формул (2.12) и (2.13) можно записать отношение правдоподо- |
|||||||||||||||||||||||||||||||||||
бия |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
2 |
|
|
|
|
|
|
n |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s |
t |
|
|
2 |
x s t |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
p |
|
|
|
(x ,...,x |
|
|
) |
|
|
|
|
|
i |
|
|
|
|
|
|
|
i |
|
i |
|
|
|
||||||
|
|
|
|
sn |
n |
|
|
|
|
i 1 |
|
|
|
|
|
i 1 |
|
|
|
|
|
|||||||||||||||
|
|
|
l |
|
1 |
|
|
|
exp |
|
|
|
exp |
|
|
|
|
. |
|
|||||||||||||||||
|
|
|
p |
|
(x ,...,x |
|
|
) |
|
N |
|
|
|
|
N |
|
|
|
|
|
||||||||||||||||
|
|
|
|
n |
n |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Переходя от квазибелого шума к белому при T = const, fc , t 0 , |
|||||||||||||||||||||||||||||||||||
получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
T |
|
|
|
|
|
|
|
|
|
2 |
T |
|
|
|
|
|
|
|
|
||||
|
|
|
|
l exp |
|
|
|
s2 (t)dt exp |
x(t)s(t)dt , |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
N0 |
0 |
|
|
|
|
|
|
|
|
N0 |
0 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
T |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
s |
(t)dt Es – энергия сигнала; |
|
x(t)s(t)dt z |
– корреляционный инте- |
|||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
грал.
С учетом этих обозначений отношение правдоподобия для полностью известного сигнала имеет вид
39
|
|
E |
s |
|
|
2z |
|
l exp |
|
exp |
|
. |
|||
|
|
N0 |
|
|
N0 |
|
|
|
|
|
|
|
|||
(2.14)
Видно, что отношение правдоподобия является монотонной функцией корреляционного интеграла. В этом случае можно перейти от сравнения с порогом l0 отношения правдоподобия l(x) к сравнению с порогом z0 значений корреляционного интеграла: z > z0 – сигнал есть; z < z0 – сигнала нет.
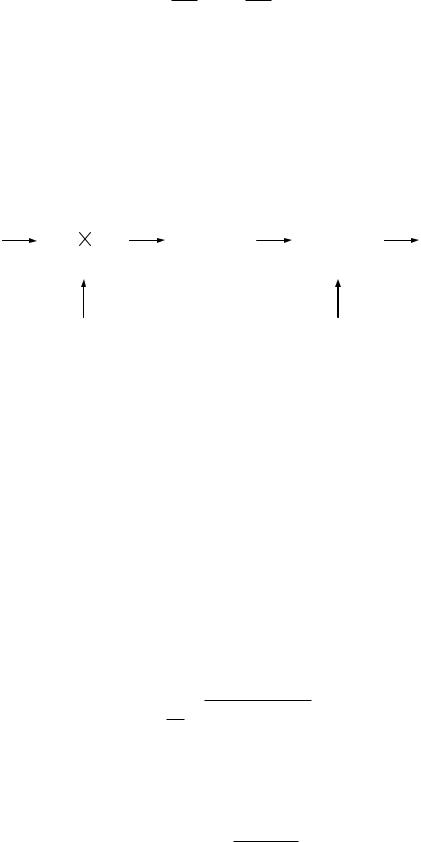
Структурная схема оптимального обнаружителя представлена на рис. 2.5, где 1 – перемножитель, 2 – интегратор, 3 – пороговое устройство.
x(t) |
1 |
|
|
2 |
|
z(t) |
3 |
|
|
|
A*1 |
|
|
|
|
|
|
|
|
|
|
A*0 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s(t) |
|
|
|
|
z0 |
||||
Рис. 2.5
Обнаружитель вычисляет корреляционный интеграл и сравнивает его с
порогом.
решение
При z > z0 принимается решение
* |
об его отсутствии. |
А0 |
А* 1
о наличии сигнала, при z < z0 –
Перемножитель и интегратор преобразуют многомерное распределение на входе обнаружителя в одномерное распределение на выходе интегратора. Поскольку операция вычисления корреляционного интеграла является линейной, при гауссовском законе распределения на входе обнаружителя значения корреляционного интеграла также будут иметь гауссовское распределение [9] . При нулевом среднем на выходе перемножителя (т. е. в тех случаях, когда полезный сигнал отсутствует) среднее значение выходного сигнала интегратора также будет равно нулю. Тогда дисперсия выходного сигнала
|
|
T |
|
2 |
2 |
2 |
|
|
|
s(t)n(t)dt |
|
|||
σ z |
zn |
|
||
|
|
|
|
|
|
|
0 |
|
|
.
Заменив квадрат интеграла произведением двух интегралов и изменив порядок интегрирования и усреднения, получим:
TT
σ2z dt s (t) s (t ) n(t) n (t ) dt .
0 0
40

В подынтегральном выражении |
n( t )n( t |
|
) есть корреляционная функция |
||||||||||||||||
|
|||||||||||||||||||
шума. Для белого шума |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
R(t t ) |
|
N |
δ(t t ). |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отсюда |
N |
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
N E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2 |
|
|
T |
T |
|
|
|
|
|
|
|
|
T |
2 |
|
|
|
|
|
|
0 |
s(t) |
|
|
|
|
dt |
|
0 |
s |
(t) dt |
0 |
s |
. |
|||||
σ z |
2 |
s (t ) (t t ) dt |
|
2 |
|
2 |
|
||||||||||||
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
В присутствии сигнала на входе обнаружителя на выходе будем иметь
T |
T |
|
T |
zsn s (t) n (t) s (t) dt s |
2 |
(t) dt s (t) n (t) dt Es |
|
|
|||
0 |
0 |
|
0 |
интегратора
zn .
Первый интеграл равен энергии сигнала, а второй – корреляционный интеграл при наличии на входе только шума. Очевидно, что тогда величина zsn распределена по гауссовскому закону со средним, равным энергии сигнала
Es, и дисперсией |
z |
. Тогда можно записать выражения для плотностей рас- |
|
2 |
|
пределения на выходе интегратора при отсутствии (pn(z)) и наличии (psn(z)) сигнала на входе:
|
|
|
1 |
|
|
|
z |
2 |
|
|
p |
n |
(z) |
exp |
|
|
|
|
; |
||
2πσ |
|
|
2 |
|
||||||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
2σ |
|
|
||
|
|
|
z |
|
|
|
z |
|
||
p |
|
(z) |
1 |
|
sn |
2πσ |
|||
|
|
|||
|
|
|
||
|
|
|
z |
exp
(z
E |
s |
) |
2 |
|
|
|
|
||
|
|
|
|
|
2 |
|
|
||
|
|
|
||
2σ |
|
|
||
z |
|
|
|
|
.
(2.15)
Отсюда аналогично формулам (2.8) и (2.10) можно получить выражения для условных вероятностей ложной тревоги и правильного обнаружения:
P |
|
F |
|
или аналогично (2.11)
1 |
1 |
Ф(u0 ) ; PD |
1 |
1 |
Ф(q u0 ) , |
|
2 |
2 |
|||||
|
|
|
|
при работе по критерию Неймана-Пирсона
(2.16)
|
|
|
|
|
|
|
P |
|
1 |
1 |
q |
1 |
2P |
) |
|||
|
|
|
|
|
|
|
|
(1 |
|||||||||
|
|
|
|
|
|
|
D |
|
|
|
2 |
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
где |
u |
0 |
|
z0 |
|
z0 2 |
|
|
|
– относительный порог регистрации; |
|||||||
σ z |
|
|
|
|
|
||||||||||||
|
N0 Ec |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
(2.16 а) q 
 2Es / N0 –
2Es / N0 –
отношение сигнал/помеха. Рассчитанные по выражениям (2.16) кривые обнаружения полностью известного сигнала (сплошные линии) при различных вероятностях ложной тревоги (10-1 и 10-4) приведены на рис. 2.6.
41
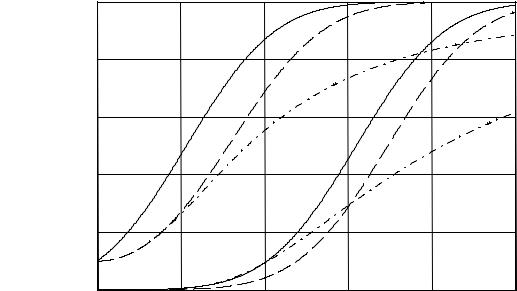
|
1 |
|
|
|
|
|
|
|
D1(1 q) 0.8 |
|
|
10 |
-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
D1(2 q) |
|
|
|
|
|
|
|
|
D2(1 |
q) 0.6 |
|
|
|
|
|
|
|
PD |
|
|
|
|
|
|
|
|
D2(2 |
q) |
|
|
|
|
|
|
|
D3(1 |
q) 0.4 |
|
|
|
|
|
|
|
D3(2 |
q) |
|
|
|
|
|
10-4 |
|
|
|
|
|
|
|
|
||
|
0.2 |
|
|
|
|
|
|
|
|
0 |
0 |
1.2 |
|
2.4 |
3.6 |
4.8 |
6 |
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
Рис. 2.6 |
|
|
|
Другим часто используемым представлением для свойств обнаружителя являются рабочие или оперативные характеристики (рис. 2.7). Оперативные характеристики показывают зависимость условной вероятности правильного обнаружения от условной вероятности ложной тревоги в соответствии с выражением (2.16 а). При этом значение отношения сигнал / помеха играет роль параметра семейства кривых. Из анализа этих характеристик следует:
1) при условной вероятности ложной тревоги PF = 0 условная вероятность правильного обнаружения PD = 0 независимо от значения отношения сигнал / помеха;
2)чем больше отношение сигнал / помеха при заданной условной вероятности ложной тревоги PF , тем больше условная вероятность правильного обнаружения PD ;
3)условная вероятность правильного обнаружения PD может быть точно равна 1 лишь при PF = 1.
Таким образом становится очевидной невозможность построения идеального обнаружителя, решающего задачу обнаружения без наличия ошибок первого и второго рода. Эти ошибки неизбежны, и следует лишь стремиться
квозможному их уменьшению. В особо ответственных ситуациях необходимо либо использовать дублирование систем обнаружения сигналов, например применяя несколько обнаружителей, работающих на разных физических
42
